Movimento de revolução das luas de Júpiter
1
Objetivos:
1. Aplicar as leis do movimento (ou 3a lei de Kepler) para calcular a massa de Júpiter.
2. Estimar o período orbital e o raio orbital para as luas galileanas de
de Júpiter.
Equipamento:
Computador com
JupLab.zip (49MB) ou
programa CLEA ``The revolutions of the moons of Jupiter'',
lápis, régua, grade para dados,
papel milimetrado, calculadora.
Introdução:
Neste exercício você irá simular a observação das quatro maiores
luas de Júpiter, as quais Galileu observou com seu telescópio no ano de
1610.
Seus nomes são Io, Europa, Ganimedes e Calisto, em ordem de distância ao
planeta.
Olhando através de um pequeno telescópio, vemos as luas alinhadas, porque
estamos enxergando o seu plano orbital de lado. À medida que o tempo passa,
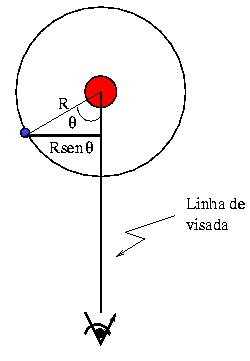
as luas se movem em torno de Júpiter em órbitas quase circulares. Mas
nós conseguimos ver apenas a componente do raio orbital que está
perpendicular à linha de visada entre Terra e Júpiter, como
na figura abaixo.
Procedimento:
- Inicializar o programa e entrar as informações do estudante
- Clique em Log In, entre seu nome em Student#, e os dos seus
colegas de grupo
(até 4 se necessário). Clique OK, e clique Yes quando
perguntar "Have you finished logging in"? Clique Start.
Vai aparecer uma tabela com alguns dados sobre a data e o período de
observação. Para alterar qualquer dado, clique duas vêzes
na caixa correspondente e então entre com o valor correto. Comece selecionando
o intervalo entre as observações de 3 horas. Quando todas
as informações estiverem de acordo, clique OK.
- Aparecerá uma tela onde Júpiter está no centro, e as luas
aparecem como pequenos pontos em ambos os lados. Pode acontecer de alguma
lua
estar atrás de Júpiter, caso em que não pode ser vista. Os dados
U.T. (tempo universal) e J.D. (dia juliano)
são listados no canto esquerdo da tela. Os dados sobre a Lua selecionada
(clicando o mouse em cima dela) se encontram no canto inferior direito: as
coordenadas x e y da lua na tela, em pixels, e a distância perpendicular
à linha de visada, que também está representada por X, em unidades
de diâmetros de Júpiter. As letras E e W indicam se a lua está a
leste ou oeste de Júpiter. Registre os
dados da primeira observação na folha de dados:
Coluna 1: Data
Coluna 2: Hora, em tempo universal
Coluna 3; Dia, em ordem numérica. Exemplo: 1, 2, 3, 4, etc, se o intervalo de
tempo entre as medidas for de 24 h; ou 1, 1.5, 2, 2.5, etc, se o
intervalo de tempo entre as medidas for 12h.
Coluna 4 - 7: posição (X = ) de cada lua. Use o sinal ``+'' para indicar
oeste, e ``-'' para indicar leste. Exemplo, se Europa foi selecionada e
tem X = 2.75W, deves escrever na coluna 5 +2,75.
- Quando tiver registrado os dados das 4 luas, clique no botão NEXT
para ir para a próxima observação.
Faça 8 observações com intervalo
de 3 horas, depois 12 observações com intervalo de 6 horas, mais 12
observações com intervalo de 12 horas e finalmente mais 8 observações com
intervalo de 24 horas. Nas observações com intervalo de 24 h meça apenas
Ganimedes e Calisto. Para mudar o intervalo entre as observações use o
botão Start.
Exemplo:
| ****(1)**** | ****(2)**** | ****(3)**** | *****(4)***** | *****(5)***** | *****(6)***** | ***** (7)***** |
| Data | Hora | Dia | Io | Europa | Ganimedes | Calisto |
| 20/abril | 0.0 | 1.0 | +2.95 | +2.75 | -7.43 | +13.15 |
| 20/abril | 12.0 | 1.5 | -0.86 | +4.70 | -6.30 | +13.15 |
Seus dados:
| ****(1)**** | ****(2)**** | ****(3)**** | *****(4)***** | *****(5)***** | *****(6)***** | ***** (7)***** |
| Data | Hora | Dia | Io | Europa | Ganimedes | Calisto |
| | | | | | |
| | | | | | |
| | | | | | |
| | | | | | |
| | | | | | |
| | | | | | |
| | | | | | |
| | | | | | |
| | | | | | |
| | | | | | |
| | | | | | |
| | | | | | |
| | | | | | |
| | | | | | |
| | | | | | |
| | | | | | |
| | | | | | |
| | | | | | |
| | | | | | |
| | | | | | |
| | | | | | |
| | | | | | |
| | | | | | |
| | | | | | |
| | | | | | |
| | | | | | |
| | | | | | |
| | | | | | |
Nota: Colete dados até ter 40 linhas de dados, sem contar os dias
nublados.
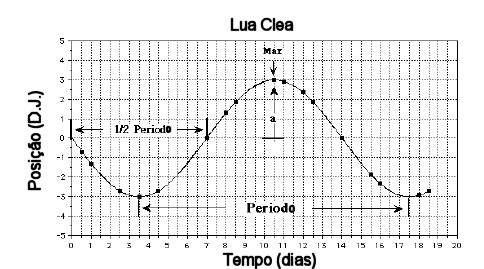
Cada ponto da curva é uma observação de uma lua fictícia chamada Clea.
- Agora você vai analisar os dados. Plotando para cada lua sua posição
em função do tempo.
Cada ponto na figura é uma observação da lua. Observe os espaçamentos
irregulares entre os pontos, devido a noites nubladas ou outros problemas.
A curva suave obtida passando uma linha entre os pontos é a curva senóide
que se obteria se a observação fosse feita a intervalos de tempo suficientemente
pequenos.
Para determinar as propriedades orbitais de cada lua, você precisa determinar
a curva senóide que melhor ajusta seus pontos.
Lembre que as órbitas das luas são regulares, portanto a forma
da curva de uma dada lua deve ser regular, passando por todos os pontos,
mantendo a mesma forma de um período para outro, mantendo o mesmo
máximo e a mesma largura.
O período da lua é o tempo que ela leva para voltar ao mesmo
ponto da órbita, portanto é o tempo entre dois máximos.
O tempo entre dois pontos com J.D. = 0 é meio período, portanto
se para alguma lua você não conseguir observar uma órbita completa,
você pode usar o meio-período para determinar o período total.
Se você, pelo contrário, tiver vários períodos em sua
curva, você pode melhorar a precisão no valor do período fazendo
a média entre eles.
Quando a lua está na máxima posição para o leste ou para oeste,
ela está na maior distância aparente do planeta. Embora as órbitas
sejam quase circulares, como nós as vemos de lado, só podemos
determinar os seu raio nessas ocasiões de máximo afastamento para um
lado ou para o outro.
Obtenção dos gráficos
-
Para desenhar os gráficos, use uma
folha de papel milimetrado.
Escolha como eixo vertical o lado
menor, e como eixo horizontal o lado maior. No eixo vertical vais marcar os
valores de posição, em diâmetros de Júpiter (DJ), com valores
entre +18 (em cima) e -18 (em baixo), numa escala 1 cm = 2 DJ
No eixo horizontal vais marcar o tempo em dias (os valores da 3a
coluna
da folha de dados), com valores entre 1 e 13, numa escala 1 cm = 0,5 dias
-
Entre todos os dados de Io com espaçamento de 3h e de 6 h.
A seguir
traçe uma curva suave entre os pontos. Marque os máximos
e mínimos com cruzes. Eles não cairão necessariamente em uma das
linhas da grade.
A curva deve ser simétrica em relação ao eixo horizontal.
Os máximos e mínimos devem ter o mesmo valor, exceto pelo sinal.
- Calcule o período (P) e o raio orbital (a). Esses valores estarão
em unidades de dias, para P e diâmetros de Júpiter para a. Converta os
valores de P para anos e de a para unidades astron^micas e use
a 3a lei de Kepler para obter a massa de Júpiter, em massas solares:
|
MJ(MSol) = |
[a(UA)]3
[P(anos)]2
|
|
|
Para Calisto: MJ = .................
Para Ganimedes: MJ = .................
Para Io: MJ = .................
Para Europa: MJ = .................
Valor médio: MJ = ................ MSol.
Cálculos:
- O que causaria um erro maior no cálculo da massa de Júpiter: 1 erro de 10%
no período ou um erro de 10% no semi-eixo maior da órbita? Por que?
-
Expresse a massa de Júpiter em massas terrestres, sabendo que a massa da Terra
é 5,9 ×1024 kg = 3 × 10-6 da
massa do Sol.
- Júpiter tem atualmente 63 satélites conhecidos. Quanto vale, aproximadamente, a razão [a(UA)]}3/[P(anos)]2 para eles?
Quanto vale essa
razão, expressando a em km e P em dias, sabendo que 1 UA tem 150 000 000 km e 1 ano tem 365,25 dias?
- Em 2003 foram descobertos 22 novos satélites de Júpiter
com períodos orbitais variando de 760 a 808 dias. Qual a distância a Júpiter
do mais próximo? E qual a distância do mais distante? Dê sua resposta em
km.
Notas:
Diâmetro de Júpiter = 142 984 km
1
CLEA -
Contemporary Laboratory Experiences in Astronomy - Department of Physics,
Gettysburg College, Gettysburg, PA 17325
Texto adaptado pelos professores Maria de Fátima Saraiva e Kepler Oliveira
 Astronomia e
Astrofísica
Astronomia e
Astrofísica

Modificada em 20 ago 2008


![]()