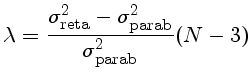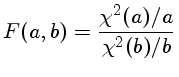Programas de transformadas e mínimos quadrados

No Fortran, as colunas 1 a 5 são reservadas para índices, a coluna 6 para marcar a continuação de uma linha, e as colunas de 7 a 72 para o código. C ou ! na primeira coluna marcam comentários. Cuide portanto que o & nos programas abaixo estejam na 6^a coluna.

Fita uma linha sem pesos. O programa (llsl.f) lê o número de pontos do arquivo de dados? Se sim, há número de pontos no arquivo de dados?
Fita uma linha com pesos mas atenção, o programa (llslw.f) com pesos lêm três colunas (x,y,w) e o arquivo dados, de exemplo, só tem 2 colunas. Use um arquivo adequado (dados3).
Fita uma parábola com pesos (parab.f)

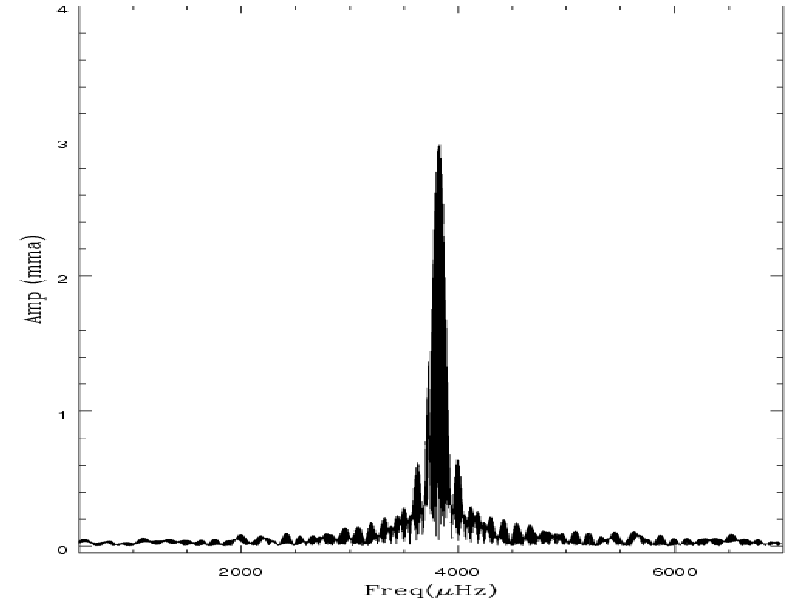
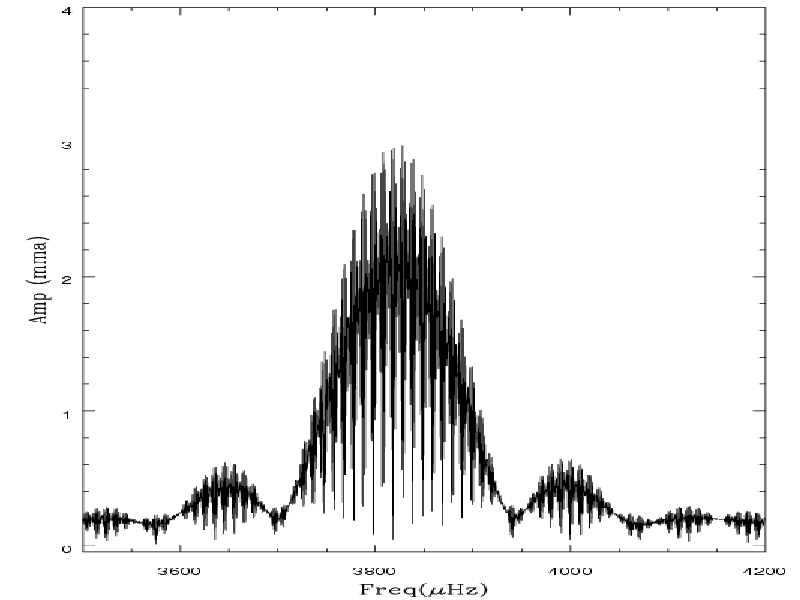
Transformada de Fourier (dft.f) - normaliza Y

C...here NORMALISES by average and makes average = 0
      YAVER = 0.0d0
      DO 4 I=1,NUM
4        YAVER = YAVER + Y(I)
      YAVER = YAVER / dble(NUM)
      DO 5 I=1,NUM
5       Y(I) = Y(I)/YAVER - 1.0
...
45    FR=0.0d0
      FI=0.0d0
        DO 50 I=1,NUM
        A=TWOPI*F*T(I)
        a=dmod(a,twopi)
        C=DCOS(A)
        S=DSIN(A)
        FR=FR+X(I)*C
50      FI=FI+X(I)*S
        FR=FR/dble(NUM)
        FI=FI/dble(NUM)
        FF=FR*FR+FI*FI
c  amplitude spectra in file outfile
      AMPLIT = 2.0d0*DSQRT(FF)

Potência Média

       avpw=0.0d0
2010  do 50 i=1,500000
      read (9,*,end=300,err=3000)x,y
        np=np+1
        avpw=avpw+y*y
50    continue
300     avpw=avpw/np
        avamp=dsqrt(avpw)

Máximos
Randomiza Tempos

Janela Espectral

c  set y equal to 1 before loop for sine (normalize to 1)
      y(i)=1.0d0
      freq=pit2/period
	do 2002 i=1,ndata
	read(1,*)time(i),dummy
      ft=freq*(time(i)-tmax)+pi2
      z=dmod(ft,pit2)
      y(i)=y(i)+amp*dsin(z)
2002  continue

Fita uma sinusoidal sem pesos (llsp.f)
Dados

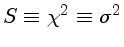Pringle, 1975 discute a necessidade de se incluir mais termos na fitagem. Para sabermos se, quando passamos de uma fitagem de uma reta para uma fitagem de uma parábola, a redução no $S\equiv \chi^2\equiv \sigma^2$ é suficiente para que o termo quadrático seja significativo, podemos definir um parâmetro

$\lambda = \frac{\sigma_{reta}^2 - \sigma_{parab}^2} {\sigma_{parab}^2}(N-3)$

e determinar o nível de confiabilidade que podemos descartar a hipótese do termo quadrático ser nulo por

$\lambda = F_p(1,n-3)$

onde o F é dado por

$F(a,b)=\frac{\chi^2(a)/a}{\chi^2(b)/b}$

F(a,b) é a variável x da função beta incompleta betai(x,df1,df2), a probabilidade de que uma variável randômica de uma distribuição beta de graus de liberdade df1 e df2 terá valor menor ou igual a x [Statistical Theory and Methodology in Science and Engineering. K. A. Brownlee. London and New York: John Wiley and Sons. 1960].

Atente que a definição usada acima é F_p[(df1-df2),df2], e não F(df1,df2), como usado em geral, onde df1 significa número de graus de liberdade da medida 1, N-k₁, sendo N o número de observações e k₁ o número de parâmetros do ajuste 1. Pringle usa F_p(1,n-3), ou seja df1-df2=1, a diferença no número de graus de liberdade quando passamos de reta para parábola. A calculadora citada usa a forma geral:

F = [σ²₁/σ²₂ * (N-k₁)/(N-k₂) - 1] * (N-k₂)

Página do CALTECH para cálculo de periodogramas por Lomb-Scargle DFT, Box Fitting Least Squares e Phase Dispersion Minimization. Se o arquivo de dados for comma-separated-values (.csv), é necessário colocar um header, tipo

NAME,RA,DEC,TIME,MAG,SIGMA,FILTER

e TIME é assumido em MJD (dias).

Astronomia e Astrofísica