Na gravitação de Newton, as órbitas periódicas são sempre elipses. Quanto maior for a massa do corpo massivo, mais próxima será a órbita, e maior a velocidade da partícula, aumentando sem limites de modo que a energia cinética compense a energia gravitacional. Para um buraco negro, a teoria de Newton prediz uma velocidade orbital acima da velocidade da luz, mas na Relatividade de Einstein nenhum corpo com massa pode atingir a velocidade da luz, muito menos ultrapassá-la. A Relatividade Geral prediz órbitas dramaticamente diferentes das elipses ou cônicas das leis de Kepler. Esta página permite a exploração destas órbitas.
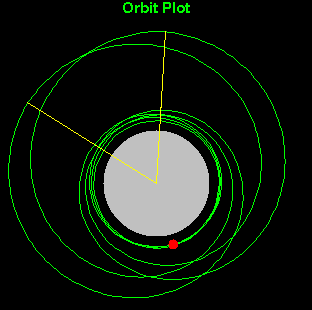 O painel da direita mostra a partícula teste orbitando
um buraco negro, visto perpendicularmente ao plano da órbita.
A órbita é desenhada com uma linha verde.
Depois de um grande número de órbitas, o gráfico torna-se complexo;
clique com o mouse em qualquer posição do painel
da direita para apagar o gráfico e recomeçar. Quando a partícula
teste alcançar sua distância máxima ao buraco negro, uma linha amarela
será desenhada a partir do centro do buraco negro até este ponto, o
apoastro da órbita. Na gravidade newtoniana, o apoastro permanece
fixo no espaço.
Os efeitos da Relatividade Geral causam
a precessão desta linha.
Você pode ver esta precessão pelo deslocamento da linha amarela.
A precessão pode ser maior que 360°;
a linha amarela mostra a precessão módulo uma órbita.
O painel da direita mostra a partícula teste orbitando
um buraco negro, visto perpendicularmente ao plano da órbita.
A órbita é desenhada com uma linha verde.
Depois de um grande número de órbitas, o gráfico torna-se complexo;
clique com o mouse em qualquer posição do painel
da direita para apagar o gráfico e recomeçar. Quando a partícula
teste alcançar sua distância máxima ao buraco negro, uma linha amarela
será desenhada a partir do centro do buraco negro até este ponto, o
apoastro da órbita. Na gravidade newtoniana, o apoastro permanece
fixo no espaço.
Os efeitos da Relatividade Geral causam
a precessão desta linha.
Você pode ver esta precessão pelo deslocamento da linha amarela.
A precessão pode ser maior que 360°;
a linha amarela mostra a precessão módulo uma órbita. 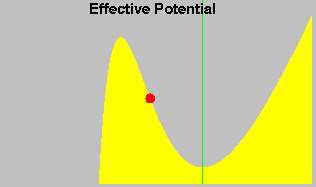 Os painéis à esquerda mostram a órbita em duas formas mais abstratas. O gráfico
do Potencial Efetivo no topo, mostra a posição da massa teste na
curva de energia gravitacional enquanto ela orbita.
O pico no lado esquerdo da curva existe apenas na Relatividade Geral - na
gravitação newtoniana a curva sobe sem limites enquanto o raio decresce,
aproximando infinito para raio=zero.
Na teoria de Einstein, a impossibilidade da partícula atingir a velocidade da
luz cria o buraco no potencial, próximo ao buraco negro.
Quando a partícula se aproxima deste pico, caindo de raios maiores com
velocidades cada vez maiores, ela permanecerá próxima
deste pico de energia por um tempo cada vez maior, enquanto a movimento
angular resultará em precessão cada vez maior.
Se a partícula passar desde pico de energia e continuar na direção de raios
menores, para a esquerda, ela cairá no buraco negro e será capturada.
Os painéis à esquerda mostram a órbita em duas formas mais abstratas. O gráfico
do Potencial Efetivo no topo, mostra a posição da massa teste na
curva de energia gravitacional enquanto ela orbita.
O pico no lado esquerdo da curva existe apenas na Relatividade Geral - na
gravitação newtoniana a curva sobe sem limites enquanto o raio decresce,
aproximando infinito para raio=zero.
Na teoria de Einstein, a impossibilidade da partícula atingir a velocidade da
luz cria o buraco no potencial, próximo ao buraco negro.
Quando a partícula se aproxima deste pico, caindo de raios maiores com
velocidades cada vez maiores, ela permanecerá próxima
deste pico de energia por um tempo cada vez maior, enquanto a movimento
angular resultará em precessão cada vez maior.
Se a partícula passar desde pico de energia e continuar na direção de raios
menores, para a esquerda, ela cairá no buraco negro e será capturada.
 O espaço-tempo em torno de um corpo gravitacional não
magnético e sem rotação é descrito pela geometria de
Schwarzschild, em que o espaço tempo é distorcido (curvado)
pela presença da massa, criando um
poço gravitacional que se estende até a
superfície do corpo, ou no caso de um buraco negro, até o horizonte de eventos.
O poço gravitacional tem a forma de um parabolóide quadridimensional em
revolução, simétrico em relação à massa central.
O gráfico inferior à esquerda mostra um secção bidimensional do
poço gravitacional. Como no gráfico superior, o lado esquerdo representa
o centro do buraco negro e a distância aumenta para a direita,
Note que a posição da partícula teste se move em sincronia nos dois gráficos,
com a mudança do raio da órbita no painel da direita.
O espaço-tempo em torno de um corpo gravitacional não
magnético e sem rotação é descrito pela geometria de
Schwarzschild, em que o espaço tempo é distorcido (curvado)
pela presença da massa, criando um
poço gravitacional que se estende até a
superfície do corpo, ou no caso de um buraco negro, até o horizonte de eventos.
O poço gravitacional tem a forma de um parabolóide quadridimensional em
revolução, simétrico em relação à massa central.
O gráfico inferior à esquerda mostra um secção bidimensional do
poço gravitacional. Como no gráfico superior, o lado esquerdo representa
o centro do buraco negro e a distância aumenta para a direita,
Note que a posição da partícula teste se move em sincronia nos dois gráficos,
com a mudança do raio da órbita no painel da direita.
O poço gravitacional de um buraco negro de Schwarzschild tem uma
garganta em um raio determinado somente pela sua massa, o
horizonte de eventos.
Qualquer matéria ou energia que cruze este horizonte é capturada.
A garganta é o ponto mais à esquerda do gráfico do poço gravitacional,
onde a inclinação da geometria parabolóide torna-se infinita
(vertical). Se a partícula tiver momentum angular suficiente, ela
pode se aproximar do horizonte de eventos, assumindo que seja
pequena o sufiente para que as forças de maré não a quebrem,
mas nunca poderá cruzar o horizonte de eventos e retornar.
Clicando sobre as várias janelas e alterando os valores nos controles, você pode explorar diferentes cenários. Para pausar uma simulação, aperte o botão Pause à direita; pressione-o novamente para retornar à simulação. Clique em qualquer parte do gráfico orbital à direita para apagar o desenho da órbita e marca de apoastro. Você pode relançar a partícula teste a qualquer distância do buraco negro (com o mesmo momentum angular), clicando na distância desejada nos gráficos de Potencial Efetivo ou Poço Gravitacional. A linha verde no gráfico de Potencial Efetivo indica a energia mínima para a qual existe uma órbita circular, para dado momentum angular.
O momentum angular é especificado na caixa à esquerda,
em termos do momentum angular por massa unitária do
buraco negro, em unidades
geométricas-- explicadas abaixo. É importante notar que, para
as órbitas dos planetas no Sistema Solar, este número é enorme;
somente nos campos gravitacionais fortes este número aproxima-se de
pequenos valores. Se o momentum angular é menor que o valor crítico
(![]() , cerca de 3,464 para um buraco negro
com massa=1 nestas unidades), nenhuma óribita estável existe;
a partícula não tem momentum angular suficiente para evitar a queda no
buraco negro.
Quando você entra com um valor menor do que este, a garganta na curva
de energia e a linha marcando a órbita circular estável desaparecem.
Qualquer que seja a distância de lançamento da partícula, ela cairá
no buraco negro.
, cerca de 3,464 para um buraco negro
com massa=1 nestas unidades), nenhuma óribita estável existe;
a partícula não tem momentum angular suficiente para evitar a queda no
buraco negro.
Quando você entra com um valor menor do que este, a garganta na curva
de energia e a linha marcando a órbita circular estável desaparecem.
Qualquer que seja a distância de lançamento da partícula, ela cairá
no buraco negro.
A caixa Mass permite que você mude a massa do buraco negro, aumentando o raio do seu horizonte de eventos. Como a forma da órbita é determinada pela razão do momentum angular pela massa, é equivalente manter a massa como 1 e mudar o momentum angular. Você pode mudar a escala de todos os painéis alterando o valor do raio máximo; este valor torna-se o ponto mais a direita nos gráficos de Potencial Efetivo e Poço Gravitacional, e a distância entre o centro do buraco negro e a borda do gráfico da órbita. quando você muda o mometum angular ou a massa, a escala muda automaticamente para mostrar a órbita estável, se ela existe.
As leis de Kepler foram fundamentais para Newton formular a lei da gravitação universal em 1687.
Enquanto as leis de Kepler se aplicam somente à orbita dos corpos em volta do Sol, ou dos satélites em torno dos planetas, a teoria de Newton permite o cálculo do efeito gravitacional e o movimento de qualquer corpo, em qualquer lugar, e as observações concordavam perfeitamente com a teoria, até que após extensas observações e cálculos exaustivos, o astrônomo Simon Newcomb concluíu em 1898 que a órbita de Mercúrio estava precessionando 43 segundos de arco por século. Esta pequena discrepância foi confirmada posteriormente. Por quase 20 anos, a precessão da órbita de Mercúrio, ou o "avanço do periélio", permaneceu uma das anomalias que demandavam explicação.
Em 1915, a Teoria da Relatividade Geral de Albert Einstein estendeu a teoria da gravitação de Newton, explicando o avanço do periélio de Mercúrio. Esta pequena discrepância na órbita de Mercúrio foi a primeira evidência que estava acima da teoria de Newton, o primeiro passo da estrada que levaria à compreensão dos buracos negros e ondas gravitacionais.
Se estamos interessados em domínios em que os efeitos relativísticos são substanciais, é mais adequado calculá-los em unidades apropriadas ao problema. Um escolha conveniente é a de unidades geométricas, obtida colocando a constante gravitational de Newton G, a velocidade da luz c, e a constante de Boltzmann k, iguais a 1. Podemos expressar qualquer das seguintes unidades como um comprimento em centímetros, multiplicando pelos seguintes fatores de conversão.
| Quantidade | Unidade | cm Equivalentes |
|---|---|---|
| Tempo | segundo | 2,997930×1010 cm/seg |
| Massa | grama | 0,7425×10-28 cm/g |
| Energia | erg | 0,826×10-49 cm/erg |
| Carga elétrica | e | 1,381×10-28 cm/e |
| Temperatura | Kelvin | 1,140×10-65 cm/K |
Os coeficientes enormes mostram que estas unidades estão muito distantes da nossa experiência diária.

O potencial gravitacional efetivo para uma partícula teste orbitando na geometria de Schwarzschild é:
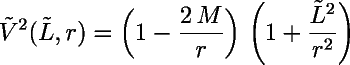
onde ![]() é o momentum angular por unidade de massa de respouso,
expresso em unidades geométricas,
M é a massa do corpo gravitacional, e r é
a distância entre a partícula teste e o centro do corpo.
é o momentum angular por unidade de massa de respouso,
expresso em unidades geométricas,
M é a massa do corpo gravitacional, e r é
a distância entre a partícula teste e o centro do corpo.
A distância de uma partícula do centro de atração envolve o tempo próprio
![]() (tempo medido por um relógio movendo-se
com a partícula)
de acordo com:
(tempo medido por um relógio movendo-se
com a partícula)
de acordo com:
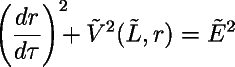
onde ![]() é a energia potencial da partícula teste,
no infinito, por unidade de massa de repouso.
é a energia potencial da partícula teste,
no infinito, por unidade de massa de repouso.
O movimento angular em torno do centro de atração é dado por:
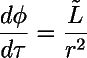
enquanto o tempo medido por um observador distante é dado por:
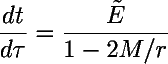
e diminui quando a distância gravitacional se aproxima do horizonte de eventos. A uma distância gravitacional de 2M, o tempo medido a uma grande distância para completamente, de modo que a partícula nunca parece alcançar o horizonte de eventos. O tempo próprio, na partícula, continua a avançar; um observador na partícula passa pelo horizonte de eventos e continua em direção à singularidade central (a não ser pela força de maré que o estraçalha).
Para encontrar os raios das órbitas circulates possíveis, diferenciamos o potencial gravitacional efetivo com relação à distância r:
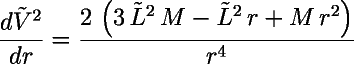
Os mínimos e máximos de uma função são os pontos em que a derivada é nula, de modo que um pouco de álgebra nos dá os raios das órbitas circulares:
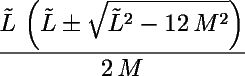
A solução maior é o raio da órbita circular estável, enquanto a de menor valor é o da solução instável no máximo. Para um buraco negro, o raio será fora do raio gravitacional 2M, enquanto para qualquer outro objeto, este raio será menor que o diâmetro do objeto, indicando que tal órbita não existe. Se o momentum angular L² é menor que 12M², nenhuma órbita estável existe; o objeto colidirá com a superfície ou, no caso de um buraco negro, atravessará o horizonte de eventos e será engolido pelo buraco negro.