Lista de Exercícios 2

Identifique no MESA ou no programa de evolução de Bodhan Paczynski (1940-2007) o passo temporal, e demonstre se é menor que o tempo do viagem do som.
Use a equação para TOP calculada por Iben e Renzini
$\log (L_{TOP}/L_\odot) &\simeq& + 1,246 -0,028 (\log Z)^2 - 0,272 \log Z - 1,073 Y$
onde é a idade do cúmulo, em unidades de anos, para estimar a idade para para:
1. Z=0,001, Y=0,24 (Extrema Pop II).
2. Z=0,02, Y=0,24 (Pop I).
A velocidade de escape de um corpo de massa M a uma distância R é dada por:

$v_{esc}^2 = \frac{2GM}{R}$

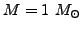Calcule o Raio de Schwarzschild, que é o raio para o qual a velocidade de escape é igual à velocidade da luz, também chamado de raio de horizonte de eventos, para $M=1~M_\odot$ .
Calcule a luminosidade, magnitude absoluta e de:
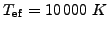1. uma anã branca com $M=1~M_\odot$ e $T_\mathrm{ef}=10\,000~K$ , R=6000 km
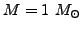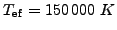2. uma anã branca com $M=1~M_\odot$ e $T_{ef}=150\,000~K$ , R=10000 km
3. uma estrela de nêutrons com 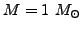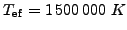$M=1~M_\odot$ , $T_{ef}=1\,500\,000~K$ , R= 10 km
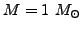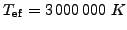4. um buraco negro, com $M=1~M_\odot$ e $T_{ef}=3\,000\,000~K$ , e raio de Schwarzschild.
5. Desenhe um diagrama HR com todas as fases evolutivas de uma estrela e coloque as estrelas calculadas acima neste diagrama. Indique no diagrama onde estão estrelas O5V, B5V, A5V, F5V, G5V, K5V, M5V, K5III e K5I.
Calcule a densidade média para:
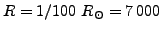1. uma anã branca com $M=0,6~M_\odot$ e raio $R=1/100~R_\odot=7\,000$ km
2. uma estrela de nêutrons com $M=1,4~M_\odot$ e raio R= 11 km
3. um nêutron, que tem massa 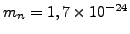$m_n = 1,7 \times 10^{-24}$ g e raio 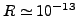$R\simeq 10^{-13}$ cm.
Use a fórmula da energia de Fermi para T=0

$E_F(T=0) = (\frac{h^2}{8m})(\frac{3n}{\pi})^\frac{2}{3}$

e para $E_F \gg mc^2$ :

$\frac{1}{E_F} = \frac{1}{E_F(T=0)}[1+\pi^2(\frac{kT}{E_F})^2 ]^\frac{1}{3}$

para calcular a Energia de Fermi para a anã branca acima, e para a estrela de nêutrons, e compare com a energia térmica, sabendo-se que a estrela de nêutrons tem $T_c \simeq 10^9$ K (queima do C) e a anã branca tem $T_c \simeq 10^8$ K (queima do He).
Calcule a velocidade média dos nêutrons em uma estrela de nêutrons.
Calcule a velocidade de escape dos nêutrons em uma estrela de nêutrons.