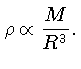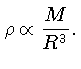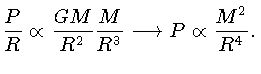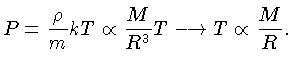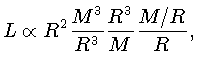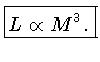Próxima: Estabilidade do Equilíbrio Térmico
Volta: Interiores Estelares
Anterior: Ordem de Grandeza da Luminosidade
No mesmo espírito, podemos usar a condição de equilíbrio
radiativo para estimar como a luminosidade de uma estrela depende da sua
massa. Usemos
Substituindo na equação de equilíbrio hidrostático (1.24),
e aproximando as derivadas pelas diferenças, encontramos:
Introduzindo estas duas proporcionalidades na equação
de estado de um gás ideal (1.25), obtemos para a temperatura:
Podemos agora substituir a proporcionalidade para 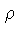 e
e 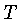 na
condição de equilíbrio radiativo (1.51),
e assumir que o coeficiente de absorção seja uma constante,
encontrando:
A dependência sobre o raio se cancela, e obtemos a relação
massa-luminosidade teórica, da maneira mais simples, indicando
que a luminosidade cresce com a terceira potência da massa.
na
condição de equilíbrio radiativo (1.51),
e assumir que o coeficiente de absorção seja uma constante,
encontrando:
A dependência sobre o raio se cancela, e obtemos a relação
massa-luminosidade teórica, da maneira mais simples, indicando
que a luminosidade cresce com a terceira potência da massa.





Próxima: Estabilidade do Equilíbrio Térmico
Volta: Interiores Estelares
Anterior: Ordem de Grandeza da Luminosidade
©
Modificada em 1999-02-25