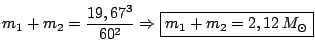Solução:
Chamando ![]() = diâmetro da Terra:
= diâmetro da Terra:
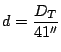
Substituindo o valor do diâmetro da Terra, em quilômetros, e passando
segundos de arco para radianos (
![]() rad):
rad):
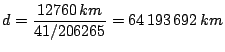
Passando para unidades astronômicas (1 UA = 1,5
![]() km):
km):
- Qual sua distância em parsecs? Em anos-luz?
- Qual seria a paralaxe de Próxima Centauri se ela fosse observada com um telescópio em Marte?
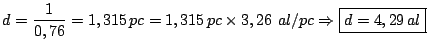
Como a distância da estrela a Marte pode ser considerada igual à distância da estrela à Terra, a variação da paralaxe só vai depender da variação do tamanho da linha de base, que é 1 UA no caso da Terra e 1,5 UA no caso de Marte. Como a paralaxe é diretamente proporcional ao tamanho da linha de base, temos:
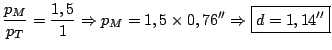
- Se eles definissem o parsec como nós o fazemos, quantas unidades
astronômicas jovianas tal parsec conteria?
Seja UAJ = unidade astronômica joviana; pcj = parsec joviano
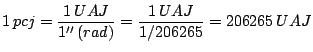
- Quantas unidades astronômicas terrestres seria igual a 1 parsec joviano?
Como o raio médio da órbita de Júpiter é 5,2 UA (unidades astronômicas terrestres),
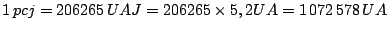
- Quantos parsecs terrestres (pc) há em 1 parsec joviano (pcj)?
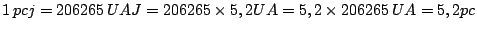
- Qual seria a paralaxe de Próxima Centauri (distância ao Sol igual a
4 anos-luz) se ela fosse observada com um telescópio em Júpiter?
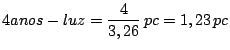
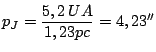
- Qual seria a sua distância, em parsecs jovianos?
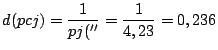
- Qual a distância da estrela?
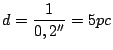
- Se essa estrela tiver uma companheira, a uma distância de 1 UA dela,
qual a separação angular entre elas?
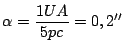
(a) 1 UA (b) 2 UA (c) 20 UA (d) 60 U (e)100 UA
Solução:
A distância (d) do sistema é:
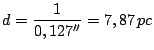
A separação entre as duas estrelas, que é igual ao semi-eixo maior da órbita relativa do sistema (a), em UA, é:
Pela 3.a lei de Kepler temos que a massa do sistema (m![]() + m
+ m![]() ), em
massas solares (M
), em
massas solares (M![]() ), é:
), é:
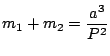
com ![]() em UA em
em UA em ![]() em anos. Logo:
em anos. Logo: