FIS02016 - Astronomia de Posição - Profa. Maria de Fátima O. Saraiva
Fenômenos do movimento diurno dos astros
Passagem meridiana de um astro
É o instante em que o astro atinge a máxima altura, ou a mínima distância zenital.
É também chamada culminação
Na passagem meridiana:
- H = 0
- A = 0° (passagem meridiana ao norte do zênite) ou A = 180° (passagem meridiana ao sul do zênite)
- z = +/-(δ - φ)
onde:
- sinal positivo indica passagem meridiano ao norte do zênite; Nesse caso a equação fica: z = declinação do astro - latitude do lugar
- sinal negativo indica passagem meridiano ao sul do zênite: z = latitude do lugar - declinação do astro
Lembrar que: latitude e declinação têm sinal negativo se for ao sul do equador, positivo se for norte
A passagem meridiana é a melhor situação para determinar a latitude
Exemplo:
Um barco perdido no oceano observa que a estrela Canopus (α = 6h 30min, δ = -52°43′), culmina ao sul do zênite com uma distância zenital de 10°. Qual a latitude do lugar?
passagem meridiana ao sul do zênite: z = -δ + φ → φ = δ + z = -52° 43′ + 10 ° = - 42° 43′
Podemos também calcular a hora sideral local:
Θ = H + α = 0 + 6h 30min = 6h 30min
Nascer e ocaso de um astro
No nascimento e no ocaso o astro se encontra sobre o horizonte, portanto:
- altura (h) = O
- distância zenital = 90°
- ângulo horário: Hnasc = - Hocaso (ou 24h - Hocaso
- O tempo decorrido entre o nascimento e a passagem meridiana é igual ao tempo decorrido entre a passagem meridiana e o ocaso, portanto, sabendo
o ângulo horário no nascimento ou no ocaso sabemos o tempo total que o astro fica acima do horizonte
-
Exemplo:
A estrela Canopus nasce, em Porto Alegre, com um ângulo horário de -9h 20min (ou +14h 40min). Quanto tempo essa estrela fica acima do horizonte em Porto Alegre?
Resposta: 2 x 9h 20 min = 18h 40 min
Estrelas circumpolares
Não têm nascer nem ocaso.
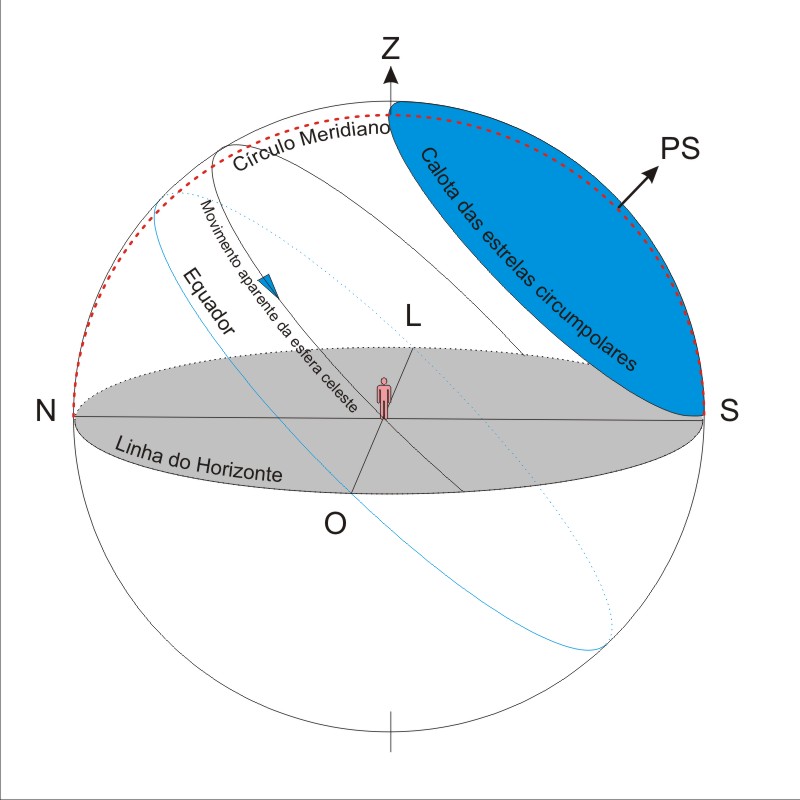
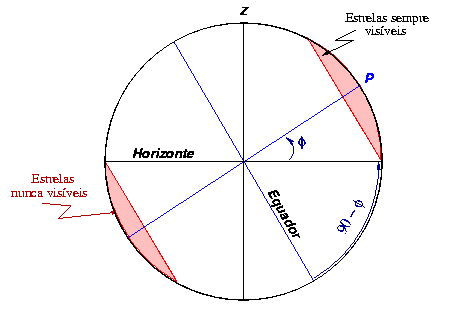
 O observador no centro da figura da esquerda, tirando uma foto do céu na sua direção sul, com várias horas de exposição, obteria uma imagem em que os traços das estrelas pareceriam o da foto da direita, tirada no observatório anglo-australiano, na Austrália.
O observador no centro da figura da esquerda, tirando uma foto do céu na sua direção sul, com várias horas de exposição, obteria uma imagem em que os traços das estrelas pareceriam o da foto da direita, tirada no observatório anglo-australiano, na Austrália.
Condição de circumpolaridade: depende da declinação da estrela e da latitude do lugar
- |δ| ≥ (90° - |φ|)
- δ e φ de mesmo sinal : estrela sempre acima do horizonte
- δ e φ de sinais opostos : estrela sempre abaixo do horizonte
As estrelas circumpolares fazem as duas culminações acima do horizonte. A latitude pode ser obtida medindo as alturas na culminação superior (hs)
e inferior (hi),
pois
φ = +/- (hi + hs)/2
onde:
- o sinal positivo vale para latitudes norte
- o sinal negativo vale para latitudes sul
 Esquema das duas culminações de uma estrela circumpolar, em um lugar de latitude norte; P é a distância polar (Δ)
Esquema das duas culminações de uma estrela circumpolar, em um lugar de latitude norte; P é a distância polar (Δ)
Exemplo1:
Qual a máxima distância polar (Δ = 90 -φ) que um astro pode ter para ser circumpolar em Porto Alegre (assuma φPoA = -30°)
Resposta: O astro tem que ter declinação negativa (sinal igual ao da latitude de Porto Alegre), com módulo δ ≥ 90 - φ= 60°, ou seja:
Δ ≤ 30 °
Exemplo2
Em um certo lugar, um observador mede as duas culminações
de uma estrela, obtendo os valores:
- culminação superior: hs = 80°; A = 180°
- culminação inferior: hi = 4 ° ; A = 180°
Qual a latitude do lugar?
Resposta: Como as duas culminações se deram ao sul do zênite (A= 180°), a estrela tem que ter declinação negativa, logo o lugar é do hemisfério sul. Portanto: φ = - (80 + 4)° /2 = - 42°
Textos completos da aula em:
Astronomia e Astrofísica e Astronomia Geodésica
 Página da disciplin
a
Página da disciplin
a
Aplicações: