Determinação da latitude e longitude do local de observação e da figura formada pela extremidade da sombra de um gnômon com dados colhidos no dia 21 de junho de 2010 em Porto Alegre

Adriano Pieres

Introdução

O presente trabalho pretende ser um resumo dos dados colhidos e analisados pela turma, juntamente com a professora, da disciplina de Astronomia de Posição, do Curso de Bacharelado em Astrofísica, da Universidade Federal do Rio Grande do Sul, no primeiro semestre do ano de 2010. A observação ocorreu no dia 21 de junho de 2010 no Parque Moinhos de Vento, em Porto Alegre. Procura também determinar, a partir dos dados a localização, no globo terrestre, através das coordenadas latitude e longitude, o ponto de observação.

Procedimento de medida e tomada de dados

As medidas propositalmente tomadas com o gnômon foram: a Hora Legal, o comprimento horizontal da sombra, e a distância mínima da reta Norte-Sul. Os pontos eram marcados com um parafuso cravado no solo, sendo posteriormente afixado um cordão

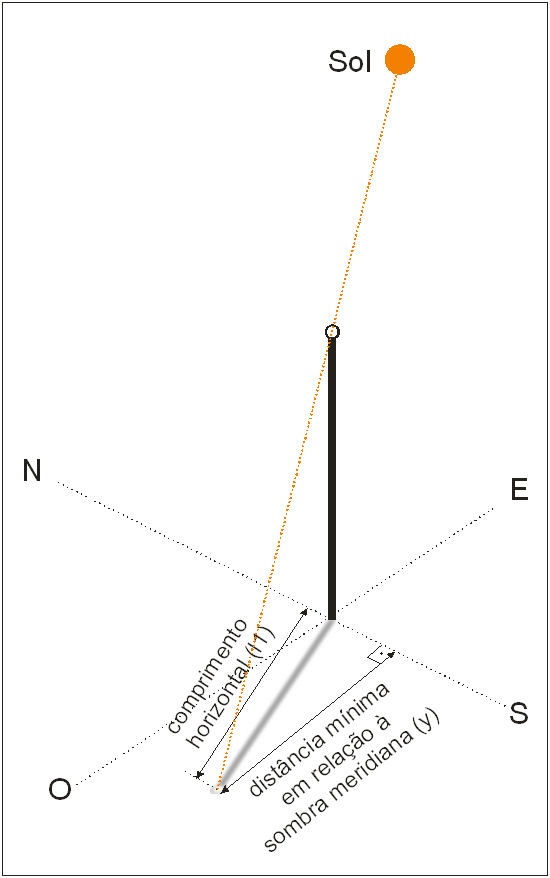
Figura 1 – Esquema ilustrativo das medidas tomadas com o gnômon, juntamente com a medida da Hora Legal.

de lã, materializando a trajetória dos raios solares naquele momento. Assim, num dado momento, geralmente espaçado em 15 minutos, se determinava, no solo o parafuso, etiquetando-o com o horário legal. Mais tarde, com a determinação da sombra mínima, e conseqüentemente, da sombra do meridiano, se pode determinar a distância mínima em relação à sombra meridiana.

Os dados obtidos com um gnômon, de altura 1,02 metros, aproximado com a vertical do lugar, durante o período de tempo em que os raios solares incidiram diretamente sobre o gnômon, livre dos elementos urbanos (árvores, prédios) foram os seguintes:

Tabela 1: Os dados obtidos com o gnômon e os elementos deduzidos

Tempo		Tempo	Compr. Horiz.	Dist. Meridiana y	Distância x	Compr. total da
Hora	Minutos	(h)	Sombra (cm)	(cm)	(cm)	sombra (cm)
9	30	9,50	245,0	-166,0	180,2	265,38
9	48	9,80	225,0	-142,0	174,5	247,04
10	0	10,00	209,0	-124,0	168,2	232,56
10	15	10,25	194,0	-106,0	162,5	219,18
10	31	10,52	183,0	-91,0	158,8	209,51
11	15	11,25	158,0	-62,0	145,3	188,06
11	30	11,50	153,0	-52,0	143,9	183,88
11	45	11,75	148,0	-39,0	142,8	179,74
12	1	12,02	144,5	-27,0	142,0	176,87
12	15	12,25	143,0	-15,5	142,2	175,65
12	25	12,42	144,0	0,0	144,0	176,47
12	45	12,75	145,0	15,0	144,2	177,28
13	0	13,00	147,5	26,0	145,2	179,33
13	15	13,25	151,0	37,0	146,4	182,22
13	30	13,50	156,0	48,0	148,4	186,39
13	45	13,75	164,0	62,0	151,8	193,13
14	0	14,00	171,0	74,0	154,2	199,11
14	30	14,50	197,0	105,0	166,7	221,84
14	45	14,75	209,0	122,0	169,7	232,56
15	0	15,00	229,0	146,0	176,4	250,69

Para uma melhor compreensão dos dados, a distância meridiana foi tomada como negativa antes da passagem meridiana e como positiva depois a tomada meridiana.

O tratamento dos dados

Plotando os dados da tabela acima (y em função de x), teremos uma reprodução da sombra da extremidade do gnômon no solo, o mais fielmente possível, como observad.:

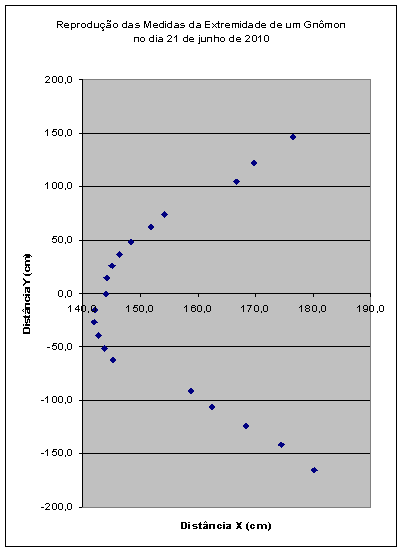
Figura 2 – O gráfico mostra uma reprodução das medidas (x é a distância Norte-Sul e y é a distância Leste-Oeste)

Se fizermos um gráfico do comprimento total da sombra em função do tempo, teremos o seguinte gráfico:

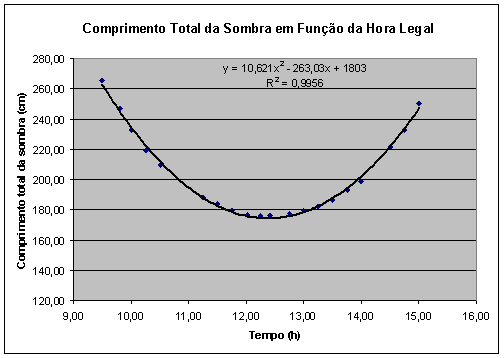
Figura 3 – O gráfico mostra o comprimento total da sombra do gnômon em relação ao tempo e a equação de melhor ajuste (r^2=0,9956) aos dados.

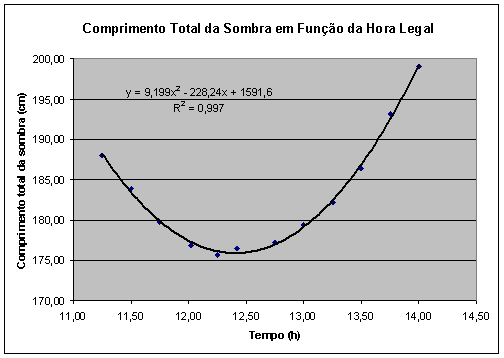
Figura 4 – O gráfico mostra o comprimento total da sombra do gnômon em relação ao tempo para os valores entre 11h e 14h, juntamente com a curva ajustada (parábola).

A determinação da Longitude

Se tomarmos os dados apenas para os instantes entre as 11h e as 14h, teremos uma aproximação o vértice da hipérbole (a figura real) com a parábola. Este arredondamento foi aplicado pois a precisão de nossas medidas era da ordem de centímetros. Como a função possui um bom ajuste (R^2=0,997), podemos, para os instantes como melhor precisão, utilizá-la para determinar o instante onde a sombra é menor. Para esta função, o instante de melhor sombra é onde a derivada da função é zero:

dy/dx = 0 = 228,24/(2x9,199) -> x = 12,4143h = 12h24min52s.

Tomando como referência as informações do local dadas pelo software Google Earth para o local (latitude:-30°01’33” e longitude: 51°12’03”O, mais precisas que a do Stellarium), teríamos a culminação superior do Sol (H(sol)=0h) na Hora Legal mais 6°12’03” = 12h 24min 48s. Conseguimos, desta forma, um erro de 4s, que corresponde à distância, no globo terrestre, de 120m, com fins de localização. Certamente não podemos atribuir o valor da precisão ao método utilizado.

A determinação da Latitude

A determinação da latitude pode ser feita levando em conta a declinação do Sol e a sombra mínima. Segundo a figura abaixo, a latitude somada com a declinação terá como cosseno a relação h/comprimento total da sombra:

Figura 5 – Esquema demonstrando a vista lateral da projeção da sombra do gnômon, quando da passagem meridiana do Sol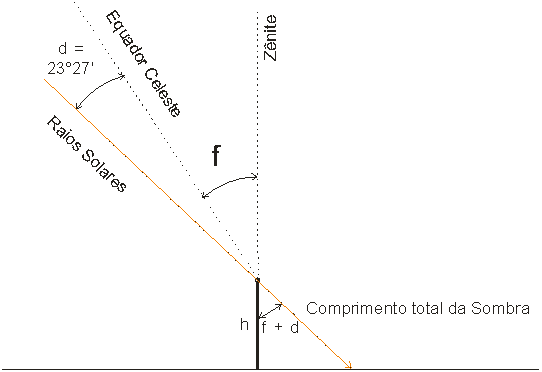

Podemos, para se ter idéia da latitude do lugar, tomarmos o menor valor tabelado do comprimento total da sombra do gnômon. O ângulo-soma da latitude com a declinação do Sol é dado como o arco cosseno da altura (h) dividido pelo comprimento total da sombra: 102/175,65. Este arco é de 54,5°. Temos uma latitude de 31,04° para o local.

Para uma medida mais acurada, devemos calcular o valor da sombra pela função do último gráfico:

y (m) = 9,199x^2 - 228,24x + 1591,6.

Como x=t=12,4143, teremos y= 175,86cm

Este valor nos fornece para a latitude do lugar um valor de arccos (102/175,86) -23,455 = 31°05’38”.

O valor tomado pelo software Google Earth é 30°1’33”. O erro é de 1°4’5”, ou de aproximadamente 120km sobre a superfície terrestre em latitude.

Vale comentar que o resultado último que tomamos teve como base erros instrumentais de precisão (verticalidade do gnômon, tomadas de medidas com pouca precisão, horizontalidade e planicidade do terreno, etc.). Se estimarmos a precisão da verticalidade do gnômon em +-2cm, igual à precisão da medida, a planicidade e horizontalidade do terreno em +-1%=2,43cm, teremos uma medida da sombra máxima entre 175,86 +-6, e um valor da latitude entre:

arccos (102/169,86) - 23,455 e arccos (102/181,86) – 23,455 = 29,6397 e 32,4289.

Determinação da figura formada pelo deslocamento das sombras devido ao deslocamento aparente do Sol na esfera celeste

A figura abaixo representa uma visão superior da esfera celeste, com o deslocamento do Sol e, por conseqüência, das sombras, durante três momentos: o solstício de inverno, o equinócio de outono e o solstício de verão para o Hemisfério Sul. O movimento solar está representado por uma linha cheia. O deslocamento das sombras ocorre na linha pontilhada. O gnômon, ao centro, aparece como um ponto, tendo em vista as suas dimensões muito menores que as demais dimensões.

As figuras são na verdade hipérboles, onde varia a sua excentricidade. O ângulo entre as assíntotas será 180°-(2 x d(sol)). Quando a declinação do Sol for zero, a excentricidade será infinita, caracterizando uma reta (equinócio). Quando o Sol passa para o outro Hemisfério, a hipérbole das sombras também passa o outro lado (não para o outro hemisfério) da projeção da sombra quando do equinócio.

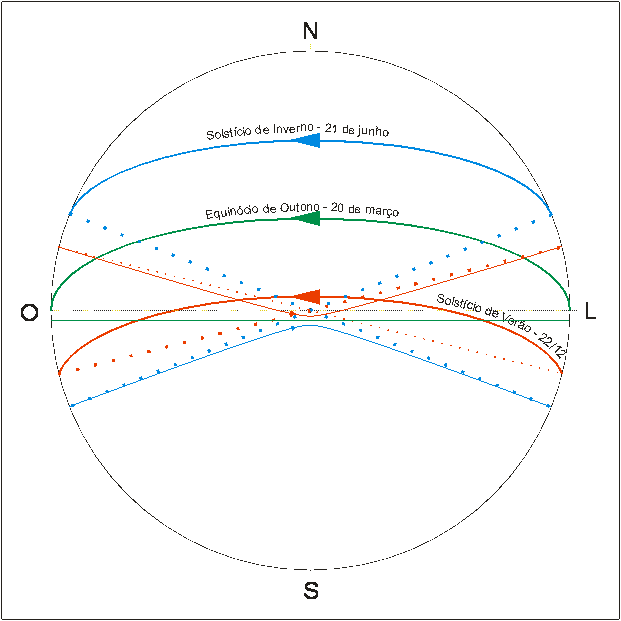
Figura 6 – Ilustração sobre a trajetória do Sol ao longo do ano e da projeção da sombra de um gnômon.

Sugestão de melhorias para a próxima tomada de medidas

Após a análise dos dados e das fontes de erros, fazemos a sugestão de tentarmos, para uma melhor localização dos dados, das seguintes ações:

- Melhor localização do gnômon, livre das sombras de árvores e prédios;

- Identificação da planicidade do terreno com um nível de bolha, ou escolha de um local pavimentado, nivelado, tal como, por exemplo, um piso de cimento reguado;

- Verticalidade aferida do gnômon, com prumo;

Uma grande fonte de erros tem sido a visualização da projeção da sombra do orifício do gnômon, de difícil resolução. Uma sugestão seria a de se colocar um anteparo, para melhor visualização da iluminação que passa pelo anteparo. Proporcionaria, pelo menos, um melhor contraste com o solo.