FIS02016 - Astronomia de Posição

Correções a serem aplicadas às medidas 1

As observações astronômicas feitas da superfície da Terra sofrem efeitos que precisam ser corrigidos, tais como Refração e Paralaxe geocêntrica. Nas observações com o Sol, em geral é necessário corrigir também pelo raio do Sol.

Refração

A curvatura dos raios luminosos provenientes de um astro ao penetrar as camadas de densidades crescentes da atmosfera causa um deslocamento aparente da posição do astro na esfera celeste, fazendo com que os corpos apareçam um pouco mais altos no céu do que realmente estão. A refração é responsável pelo achatamento da Lua e do Sol no horizonte, e também pelo fato de podermos ver o Solquando ele já está abaixo do horizonte.

No pôr do sol, a margem inferior do Sol aparece, em média, 35′ mais alto do que realmente está, mas a margem superior do Sol, que está mais longe do horizonte, aparece apenas 29′ mais elevada do que o real. O achatamento, portanto, é de 6′, em torno de 1/5 do diâmetro do Sol.

Como mostra a figura abaixo, a posição real do astro seria S, mas o observador o enxerga em S′. O ângulo entre OS e OS′ é a refração astronômica.


Supondo uma atmosfera de camadas plano-paralelas (que pode ser usada com aproximação razoável para distâncias zenitais até 65°), como mostra a próxima figura, pode-se obter uma fórmula simples de refração.

Seja:
z′: distância zenital aparente
z: distância zenital real
R: correção da refração.

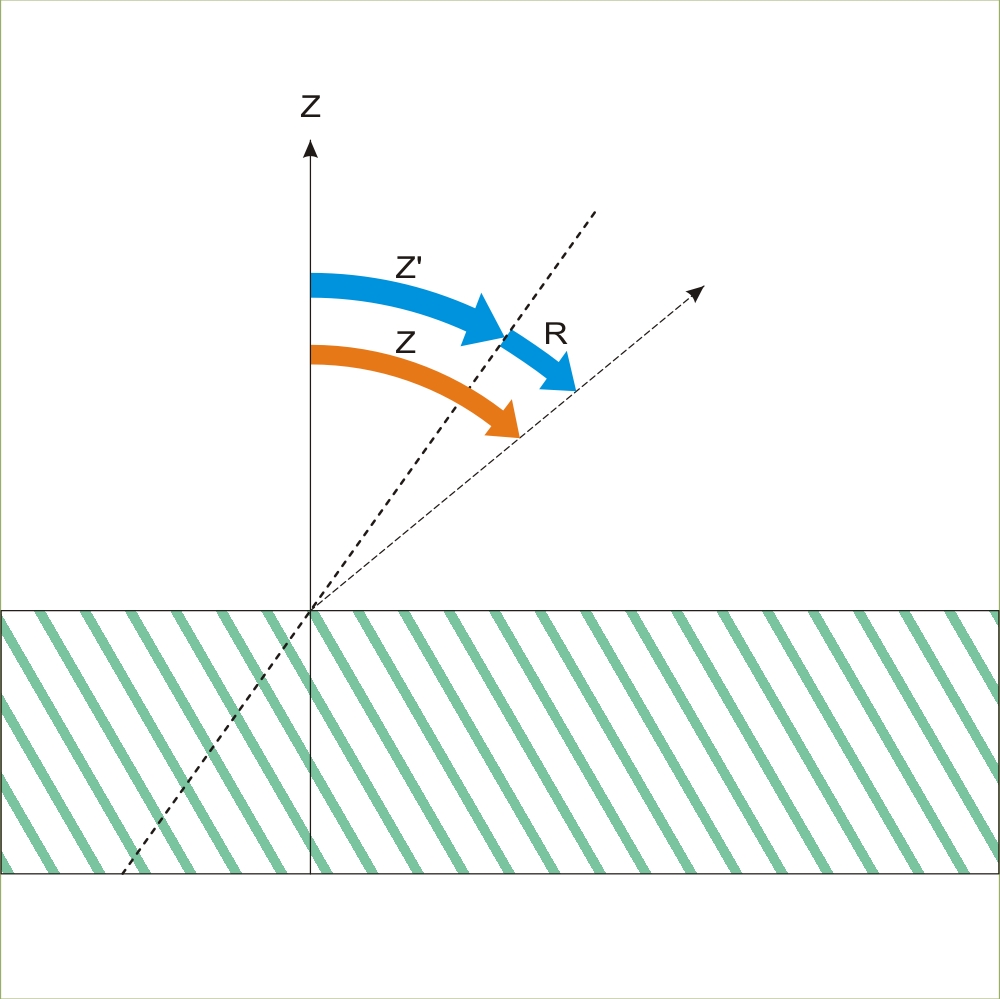
Da figura vemos que z = z′+ R     (1)

Sendo
n: índice de refração próximo ao solo
temos:
sen z = n sen z′    (2)

Substituindo (1) em (2), e fazendo a aproximação para R muito pequeno (sen R = R; cos R = 1), obtemos:
R cos z′= (n-1) senz′
R = (n-1) tan z′

O índice de refração depende da temperatura e da pressão. Para condições normais (T = 20 C e P = 760 mmHg), n=1,000290. Nesse caso, temos a refração normal, Ro, dada por
Ro = 0,000290 rad × tan z′
Como 1 rad = 360 °/2π×3600′′/°= 206265′′ → 0,000290 rad × 206265′′/rad = 60′′

Logo a correção por refração é dada por
Ro = 60′′ tan z′ ou Ro = 1′ tan z′

Os anuários astronómicos do Observatório Nacional e do Instituto Astronômico e Geof&iucute;sico da USP fornecem tabelas com valores da refração normal e as correções por variações de temperatura e pressão.
A correção por refração é sempre aditiva, isto é, z ≥ z′ em todos os casos.

z = z′ + 60′′ tan z′ ou z = z′ + 1′ tan z′

Paralaxe geocêntrica

Chama-se paralaxe geocêntrica o desvio que sofre a direção de um astro qualquer em relação à posição que ele teria se fosse observado do centro da Terra.
As posiçõs dos astros dadas nos anuários se referem ao centro da Terra, ao qual devem ser referidas as observações feitas de uma ponto qualquer da superfície da Terra.
A figura abaixo mostra que, sendo L um lugar qualquer na superfície da Terra, o ângulo SLS′ mede o desvio paraláctico, o qual depende da posição do astro em relação à direção LC, que nada mais é do que a vertical do lugar.

Influência da paralaxe geocéntrica sobre as distâncias zenitais medidas

Seja C o centro da Terra, suposta esférica, L o lugar de observação, S o astro e LZ a direção do zênite. O ângulo ZCS é a distância zenital verdadeira e ZLC a distância zenital afetada de paralaxe. Δ é a disância do astro em relaço ao centro da Terra.

Considerando a figura acima, do triângulo CLS tiramos:

sen P/R = sen (180°- z′)/Δ

Como sen (180°- z′) = sen z′,

Temos: sen P = R sen z′/Δ

Fazendo a aproximação para P pequeno (sen P = P)

Ficamos com:

P = R sen z′/Δ

O valor máximo de P será o correspondente a z′ = 90°. Esse valor é chamado paralaxe horizontal Po, pois é a paralaxe para o astro no horizonte.
  Po = R sen 90°/Δ = R/Δ → R=Po.Δ → P = Po sen z′

Conforme se nota no triângulo CLS, z = z′ - P, ou seja, a correção de paralaxe é sempre subtrativa.

Pela figura vemos que sen Po = CL/CSo, onde CL é o raio da Terra e CSo é a distância do astro ao centro da Terra.
No caso do Sol, sua distância média à Terra é 150 milhões de km (1,5 × 108 km), e o raio da Terra é 6370 km. Temos então que a paralaxe horizontal do Sol é 8,8′′

Correção pelo raio do Sol

As coordenadas do Sol dadas pelos anuários são coordenadas do centro do Sol. Assim, também devemos referir nossas observações ao centro do Sol. Se forem feitas observações dos bordos opostos do Sol, a sua média aritmética dá as coordenadas do centro do Sol. Mas se for feita a visada de um único bordo do Sol, deve ser feita a correção no azimute e na distância zenital.

A correção em distância zenital será simplesmente +/- R☉ (raio angular aparente do Sol) conforme se observa o bordo superior (+), ou inferior (-), ou seja:

z = z′ +/- R☉

Exercícios:

  1. Em um certo dia a Terra se encontra a 152 300 000 km do Sol. Qual o raio aparente do Sol nesse dia?
  2. Qual a paralaxe horizontal do Sol nesse dia?
  3. Qual a diferença devido à refração entre a distância zenital verdadeira e a distância zenital medida para um astro que se encontra a 65° do zênite? E um astro que se encontra no zênite?
  4. A distância média da Lua à Terra é de 384 000 km. Qual a paralaxe horizontal da Lua?
  5. Qual o raio aparente médio da Lua?

1 Texto baseado na apostila de Astronomia de Posição do prof. José Carlos Haertel (Escola de Engenharia da UFRGS, 1957).
Figuras: Adriano Pieres


  Volta Página da disciplina