Dedução da força diferencial

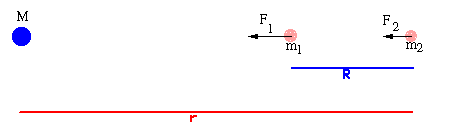
Considere as duas partículas da figura acima. Chamemos de R a distância entre as duas partículas, e de r a distância de M à partícula m₂. O valor de será:

Sendo:

Temos que:

$F_1 - F_2 = GM{[\frac{m_1}{{(r-R)}^2} - \frac{m_2}{r^2}]}$

Considerando e elemento de massa m₁ = m₂ = m, podemos escrever:

Para grande distância ao corpo massivo M, r ≫ R,

, e

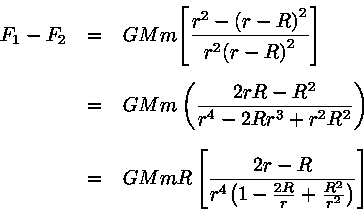
Portanto a expressão da força diferencial fica:

Podemos chegar a esse mesmo resultado tomando a derivada da Lei de Gravitação Universal:

massa de prova Então:

Esta é a expressão da força diferencial dF na direção de dr. É basicamente a mesma expressão derivada acima, com a diferença de que aqui temos dr onde acima lá temos R. Isso nos diz portanto que dr é a separação entre os pontos para os quais estamos calculando a força diferencial.

Próxima: Marés Volta: Forças Gravitacionais Diferenciais

Astronomia e Astrofísica