Marés, fases da Lua e bebês
Versão ampliada do artigo A LUA E OS BEBÊS, publicado em Ciência Hoje, Rio de Janeiro, vol.29, n. 170: p. 47; abril de 2001
Fernando Lang da Silveira
Universidade Federal do Rio Grande do Sul - UFRGS
Instituto de Física
Caixa Postal 15051 - 91501-970 - Porto Alegre, RS - Brasil
Endereço eletrônico:lang@if.ufrgs.br
Resumo. Os mecanismos responsáveis pelas marés são discutidos; demonstra-se que tanto a Lua, quanto o Sol são responsáveis pelos efeitos de maré nos oceanos. Apesar da força gravitacional do Sol na Terra ser aproximadamente 200 vezes maior do que a da Lua, os efeitos solares de maré são aproximadamente 2 vezes menores do que os lunares. Apresenta-se um estudo com 93124 datas de nascimento, visando encontrar indícios a favor ou contra a alegada influência da Lua sobre o nascimento de bebês.
1. - Introdução
São muitas as crenças populares que relacionam as fases da Lua com acontecimentos terrenos. Não poderiam faltar aquelas que se referem ao nascimento de bebês. É comum ouvir-se afirmações tais como: "Nascem mais bebês nos dias de mudança de fase da Lua!" ou "Nascem mais bebês na Lua Cheia!". Recentemente escutei um programa radiofônico no qual uma astróloga usou o seguinte argumento: "Se a Lua é capaz de agir nas enormes massas de água dos oceanos, como ela não teria efeito sobre os líquidos no útero da mãe ou sobre outros fluidos corporais, influenciando no crescimento dos nossos cabelos?". Sem dúvida, um persuasivo argumento, especialmente para quem desconhece como as marés ocorrem. As pessoas sabem que as marés existem; muitas já as observaram no mar, nunca, porém, em uma bacia ou em um açude.
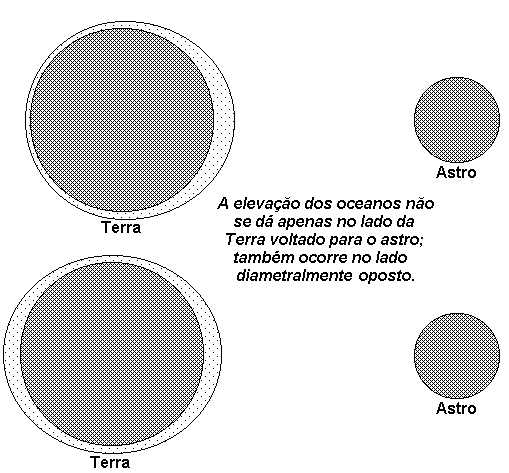
Neste trabalho inicialmente explicaremos como ocorrem as marés. A astróloga centrou o seu argumento na Lua, parecendo desconhecer que o Sol contribui com cerca de um terço do efeito total de maré. A compreensão destes mecanismos1 ajudará a entender a razão pela qual não poderíamos observar marés em pequenas porções de água como um açude. Adicionalmente compreenderemos que a elevação dos oceanos não se dá apenas no lado da Terra voltado para o astro (concepção errada), mas também no lado diametralmente oposto. A figura 1 representa a concepção errada e a correta sobre as marés; é importante destacar que a espessura dos oceanos está muito exagerada, não guardando relação de escala com o raio da Terra (as maiores profundidades oceânicas são da ordem de 10 km; o raio da Terra é aproximadamente 6400 km; como veremos adiante o desnível médio entre a maré alta e baixa é de apenas 1m).

Figura 1 - Concepção errada e correta sobre as marés.
No final deste trabalho apresentaremos um estudo com 93124 datas de nascimento, visando encontrar indícios a favor ou contra a alegada influência da Lua sobre o nascimento de bebês.
2. - Como ocorrem as marés
Na Terra, as marés devem-se ao fato do campo gravitacional de um dado astro2 (a Lua, o Sol ou qualquer outro corpo do sistema solar) na região ocupada pelo planeta não ser uniforme, isto é, as ações do astro sobre a Terra são diferentes em diferentes pontos dela. Para compreendermos isto, começaremos com um sistema muito simples e extremamente idealizado.
2. 1 - Sistema de três corpos em um campo gravitacional não-uniforme
Por simplicidade, imaginemos três corpos (partículas) com a massa de 1 kg, submetidos a um campo gravitacional não-uniforme. Suponhamos que o campo gravitacional3 sobre os três corpos tenha a mesma orientação mas varie em intensidade, conforme representado na figura 2. O corpo que produz tal campo não está representado na figura 2, podendo ser imaginado à direita dos três corpos.
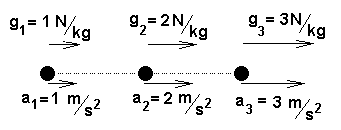
Figura 2 - Três corpos de 1 kg submetidos a um campo gravitacional não-uniforme sofrem acelerações diferentes.
A figura 2 também representa, para cada um dos corpos, a aceleração por ele sofrida, obtida imediatamente da aplicação das Leis de Newton. Por exemplo, visto que a força gravitacional4 sobre o corpo 3 tem intensidade de 3 N (![]() ), esta produz a aceleração de
), esta produz a aceleração de ![]() (
(![]() ). Supondo-se que, inicialmente, cada um dos três corpos esteja em repouso em relação aos demais, é fácil de se concluir que o afastamento entre eles irá variar, pois logo em seguida não mais estarão em repouso, deslocando-se com diferentes velocidades.
). Supondo-se que, inicialmente, cada um dos três corpos esteja em repouso em relação aos demais, é fácil de se concluir que o afastamento entre eles irá variar, pois logo em seguida não mais estarão em repouso, deslocando-se com diferentes velocidades.
Suponhamos agora que os três corpos estejam ligados por hastes finas e leves, conforme a figura 3. Assim as distâncias relativas não podem ser alteradas, o que significa dizer que os três corpos devem sofrer a mesma aceleração. Esta é facilmente calculável, bastando que dividamos a força gravitacional resultante sobre o sistema (![]() ) pela massa do sistema (3 kg); obtém-se desta forma a aceleração de
) pela massa do sistema (3 kg); obtém-se desta forma a aceleração de ![]() .
.
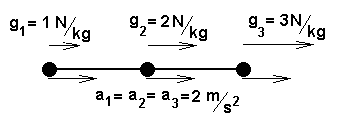
Figura 3 - Três corpos de 1 kg, ligados por hastes leves, submetidos a um campo gravitacional não-uniforme, sofrem a mesma aceleração.
Para que os três corpos sofram a mesma aceleração, as hastes que os unem devem estar tensionadas. O corpo 3, sob a ação da força produzida pelo campo gravitacional (3 N), teria aceleração de ![]() ; todavia, sofre uma aceleração menor (
; todavia, sofre uma aceleração menor (![]() ). Para que isto ocorra, deve haver uma força exercida pela haste sobre o corpo 3, orientada para a esquerda. Sobre o corpo 1, que tem uma aceleração maior (
). Para que isto ocorra, deve haver uma força exercida pela haste sobre o corpo 3, orientada para a esquerda. Sobre o corpo 1, que tem uma aceleração maior (![]() ) do que a produzida pelo campo gravitacional (
) do que a produzida pelo campo gravitacional (![]() ), deve existir uma força, devida à haste, para a direita. Este exemplo numérico mostra que um campo gravitacional não-uniforme aplicado sobre um sistema extenso, determina o aparecimento de forças internas ao sistema. Qualquer sistema real (por exemplo, a Terra) não é rígido e, portanto, a ocorrência dessas forças internas, devidas à não-uniformidade do campo gravitacional externo (por exemplo, devido ao Sol ou à Lua), estarão associadas a deformações do sistema (as marés).
), deve existir uma força, devida à haste, para a direita. Este exemplo numérico mostra que um campo gravitacional não-uniforme aplicado sobre um sistema extenso, determina o aparecimento de forças internas ao sistema. Qualquer sistema real (por exemplo, a Terra) não é rígido e, portanto, a ocorrência dessas forças internas, devidas à não-uniformidade do campo gravitacional externo (por exemplo, devido ao Sol ou à Lua), estarão associadas a deformações do sistema (as marés).
Uma outra maneira de tratarmos o sistema na situação da figura 3 é aplicando as Leis de Newton em um referencial acelerado; em referenciais acelerados cada corpo sofre, além das forças reais (forças causadas por outros corpos), a chamada força fictícia ou inercial (que não é causada por outro corpo). A força inercial sobre cada corpo tem sentido contrário ao da aceleração do referencial e seu módulo é igual à massa do corpo multiplicada pela aceleração do referencial. Se escolhermos como referencial o próprio sistema (isto é extremamente conveniente pois então todos os três corpos encontram-se em repouso, ou seja a situação é estática), e como todos os corpos têm a mesma massa, sobre cada um deles há uma força inercial de 2 N (![]() ), dirigida para a esquerda (em sentido contrário ao da aceleração do referencial). A figura 4 representa, sobre cada um dos três corpos, a força devida ao campo gravitacional (
), dirigida para a esquerda (em sentido contrário ao da aceleração do referencial). A figura 4 representa, sobre cada um dos três corpos, a força devida ao campo gravitacional (![]() ) externo ao sistema, que rotulamos com um índice j (j =1 ou 2 ou 3), e a força inercial que ocorre no referencial acelerado do próprio sistema (
) externo ao sistema, que rotulamos com um índice j (j =1 ou 2 ou 3), e a força inercial que ocorre no referencial acelerado do próprio sistema (![]() ); nesta figura não estão representadas as forças internas ao sistema (as forças tensoras nas hastes).
); nesta figura não estão representadas as forças internas ao sistema (as forças tensoras nas hastes).
|
|
Figura 4 - Força gravitacional (para a direita) e força inercial (para a esquerda) no referencial acelerado, aplicadas a cada um dos corpos do sistema.
Isto posto, podemos definir o que é a força de maré sobre qualquer corpo do sistema (![]() ): é a resultante da soma vetorial da força gravitacional, devida ao campo gravitacional externo, com a força inercial, no referencial acelerado do sistema. Ou seja:
): é a resultante da soma vetorial da força gravitacional, devida ao campo gravitacional externo, com a força inercial, no referencial acelerado do sistema. Ou seja:
|
|
(1) |
Aplicando tal definição a cada um dos três corpos do nosso sistema, encontraremos o que está representado na figura 5.
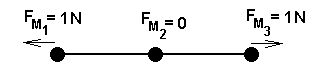
Figura 5 - Força de maré sobre cada um dos corpos do sistema.
Nesta altura é importante ressaltar que a representação da figura 5 é válida apenas no referencial do sistema, no qual cada um dos corpos se encontra em repouso. Isto é possível graças a forças internas ao sistema (neste caso, forças tensoras nas hastes) não indicadas na figura. O sistema está acelerado para a direita devido ao campo gravitacional externo. Se admitirmos que as hastes não são rígidas, é fácil concluir que elas serão deformadas devido às forças de maré ![]() e
e ![]() .
.
Até este ponto a dedução feita nos auxilia a entender a origem das forças de maré num singelo sistema de três partículas imersas em um campo gravitacional não-uniforme. A seguir discutiremos as forças de maré em uma situação mais realística.
2. 2 - Forças gravitacionais do Sol e da Lua na Terra
Se admitirmos que o Sol e a Terra são corpos com distribuição esférica de massa, poderemos calcular o módulo da força gravitacional que o Sol exerce sobre a Terra pela Lei da Gravitação Universal:
|
|
(2) |
onde G é a constante da gravitação universal, ![]() é a massa da Terra,
é a massa da Terra, ![]() é a massa do Sol e
é a massa do Sol e ![]() é a distância Terra- Sol.
é a distância Terra- Sol.
Em seguida, utilizando a Segunda Lei de Newton, calculamos a aceleração que a Terra sofre devido à ação gravitacional do Sol.
|
|
(3) |
A Lua exerce uma força gravitacional sobre a Terra, acelerando-a também. Assim, é fácil de se obter a aceleração que a Terra sofre por parte da Lua, bastando que, na equação 3, a massa do Sol seja substituída pela da Lua e a distância Terra- Sol seja substituída pela distância Terra- Lua. Obtém-se então:
|
|
(4) |
Desta forma, a aceleração que a Terra sofre devido ao campo gravitacional do Sol, não depende da massa da Terra. Sabendo que ![]() ,
, ![]() e que
e que ![]() , a equação (3) fornece para a aceleração que a Terra sofre devido ao Sol o seguinte valor:
, a equação (3) fornece para a aceleração que a Terra sofre devido ao Sol o seguinte valor:
|
|
(5) |
Esta aceleração, apesar de muito pequena quando comparada às acelerações de corpos que caem próximos à superfície da Terra, é responsável por manter a Terra em sua trajetória anual em torno do Sol.
Sabendo-se que ![]() e que
e que ![]() , pode-se determinar, utilizando a equação (4), o seguinte valor da aceleração da Terra produzida pela Lua:
, pode-se determinar, utilizando a equação (4), o seguinte valor da aceleração da Terra produzida pela Lua:
|
|
(6) |
A aceleração da Terra produzida pela Lua é quase 200 vezes menor do que a produzida pelo Sol. Ou seja, a força gravitacional do Sol sobre a Terra é quase 200 vezes maior do que a da Lua. Apesar de pequena, a aceleração produzida pela Lua sobre a Terra é importante para o movimento do sistema Terra- Lua. Ela é responsável por fazer com que o centro de massa da Terra descreva uma trajetória aproximadamente circular em torno do centro de massa do sistema Terra- Lua5. A figura 6 representa movimento do sistema Terra- Lua. Tanto a Terra quanto a Lua descrevem órbitas aproximadamente circulares em torno do centro de massa (CM) deste sistema, com período de 27,3 dias. O centro de massa do sistema Terra- Lua situa-se a aproximadamente 0,74 raios terrestres do centro da Terra.
|
|
Figura 6 - A Terra e Lua orbitam em torno do centro de massa do sistema Terra- Lua.
Veremos a seguir que apesar de a aceleração produzida pela Lua na Terra ser aproximadamente 200 vezes menor do que a aceleração produzida pelo Sol na Terra, as forças de maré lunares são aproximadamente 2 vezes maiores do que as solares.
2. 3 - Forças de maré lunar e solar na Terra
Para calcularmos a força de maré lunar sobre um corpo (partícula) de massa m em um ponto da Terra, devemos encontrar a resultante da soma da força gravitacional que a Lua exerce com a força inercial no sistema de referência da Terra, acelerado pela Lua, sobre este corpo. A figura 7 representa, em diversos pontos da Terra, as duas forças sobre um corpo de massa m; a força inercial em qualquer ponto da Terra tem sempre a mesma orientação e intensidade pois ela depende apenas da massa do corpo e da aceleração do referencial. A aceleração do referencial é a aceleração do centro de massa da Terra, produzida pela Lua; como esta aceleração aponta para a Lua, a força inercial sobre um corpo de massa m será sempre a mesma, com sentido contrário ao da aceleração do referencial. O que varia de ponto para ponto da Terra é a força gravitacional com a qual a Lua atrai um corpo de massa m na Terra.
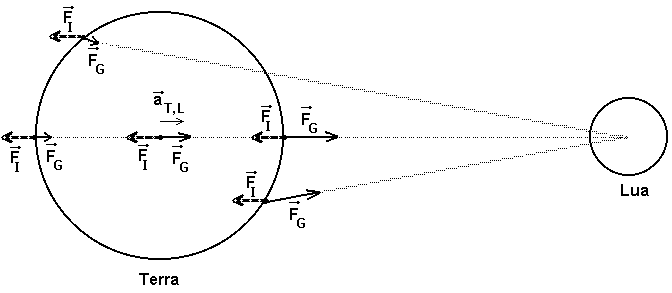
Figura 7 - Representação das forças gravitacional da Lua e inercial, sobre um corpo de massa m, em diversos pontos da Terra.
Note-se que no centro da Terra as duas forças se cancelam; em qualquer outro ponto haverá uma resultante e, consequentemente, força de maré. A força de maré de maior intensidade ocorre sobre a linha que une os centros do planeta e do satélite, apontando para fora da Terra. A figura 8 representa a força de maré (apenas a resultante das duas forças) em diversos pontos da Terra e não só naqueles representados na figura 7.
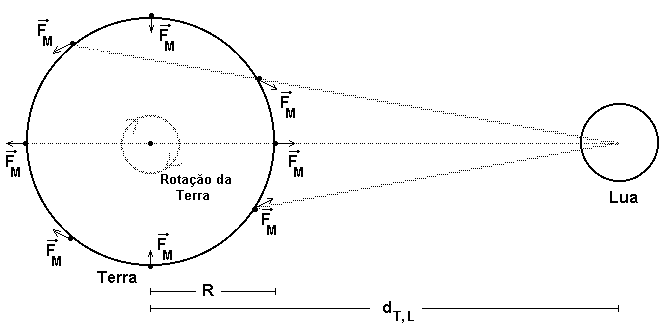
Figura 8 - Representação da força de maré lunar em diversos pontos da Terra.
Na figura 8 pode-se observar que na direção ortogonal ao eixo que une o centro do planeta e de seu satélite, a força de maré está dirigida para o centro da Terra.
É importante destacar que o eixo de rotação da Terra é quase perpendicular ao plano da figura 8; o sentido da rotação da Terra, indicado na figura, é aquele visto do hemisfério sul.
Determinaremos, a seguir, a intensidade da força de maré na superfície da Terra, sobre a linha que une o centro do planeta e seu satélite, no lado voltado para a Lua. Como a força gravitacional e a força inercial sobre um corpo de massa m têm sentidos contrários, a intensidade da força de maré (![]() ) é encontrada subtraindo-se da intensidade da força gravitacional (
) é encontrada subtraindo-se da intensidade da força gravitacional (![]() )a intensidade da força inercial (
)a intensidade da força inercial (![]() ), isto é:
), isto é:
|
|
(7) |
A intensidade da força gravitacional é dada pela Lei da Gravitação Universal; a intensidade da força inercial é o produto da massa do corpo (m) pela aceleração do referencial, isto é, a aceleração do centro de massa da Terra produzida pela Lua, cuja expressão foi apresentada na equação (4). Podemos portanto escrever a equação (7) como se segue:
|
|
(8) |
sendo ![]() a real separação entre o lado da Terra mais próximo da Lua e o centro da Lua. Procurando o denominador comum da equação (8), obtém-se:
a real separação entre o lado da Terra mais próximo da Lua e o centro da Lua. Procurando o denominador comum da equação (8), obtém-se:
|
|
(9) |
|
|
(10) |
|
|
(11) |
Ou ainda:
|
|
(12) |
Como ![]() , temos que
, temos que ![]() , donde obtemos o seguinte valor aproximado para a força de maré:
, donde obtemos o seguinte valor aproximado para a força de maré:
|
|
(13) |
Pode-se também demonstrar que a intensidade da força de maré no outro lado da Terra, isto é, no ponto da Terra mais afastado da Lua (isto é, a uma distância![]() do centro da Lua), também é dada pela equação (13) (em qualquer outro ponto da Terra ela é menos intensa). Se calcularmos a força de maré no local da Terra onde ela é mínima e está dirigida para o centro do planeta (vide figura 8), resulta em:
do centro da Lua), também é dada pela equação (13) (em qualquer outro ponto da Terra ela é menos intensa). Se calcularmos a força de maré no local da Terra onde ela é mínima e está dirigida para o centro do planeta (vide figura 8), resulta em:
|
|
(14) |
Portanto, a força de maré máxima tem o dobro da intensidade da força de maré mínima.
As equações (13) e (14) também pode ser utilizada para se calcular a força de maré solar, bastando que se substitua a massa da Lua pela massa do Sol e a distância Terra- Lua pela distância Terra- Sol.
Calculando, pela equação (13), a intensidade da força de maré lunar máxima sobre um corpo de 1 kg, encontramos ![]() ; para a força de maré solar encontra-se
; para a força de maré solar encontra-se ![]() . Desta forma, apesar da força gravitacional do Sol sobre a Terra ser cerca de 200 vezes maior do que a da Lua, a força de maré solar perfaz menos da metade da força de maré lunar6.
. Desta forma, apesar da força gravitacional do Sol sobre a Terra ser cerca de 200 vezes maior do que a da Lua, a força de maré solar perfaz menos da metade da força de maré lunar6.
2.4 - Composição das forças de maré lunar e solar
Na figura 9 é apresentado um típico diagrama utilizado para explicar as fases da Lua, representando-a em movimento de translação circular uniforme em torno da Terra; a parte da Terra que ali aparece é o hemisfério norte7, que gira diurnamente em torno de seu próprio eixo no sentido anti-horário (mesmo sentido da translação da Lua em torno da Terra). O Sol, muito distante, ilumina a região do sistema Terra- Lua com raios luminosos praticamente paralelos entre si, mas não exatamente paralelos ao plano da órbita da Lua.
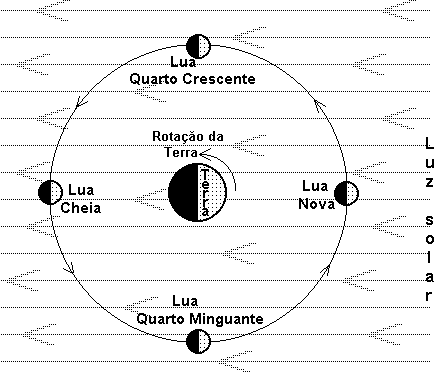
Figura 9 - Lua em órbita circular em torno da Terra.
O plano da órbita da Lua em torno da Terra se inclina aproximadamente 5 graus em relação ao plano da órbita da Terra em torno do Sol (eclíptica), conforme representa a figura 10 (para que esse ângulo possa ser representado na figura, exageramos sua abertura). Caso esses dois planos coincidissem, a cada Nova ocorreria um eclipse do Sol e a cada Cheia ocorreria um eclipse da Lua. Os eclipses somente são possíveis quando a Lua, na fase Nova ou Cheia, estiver próxima a um dos dois pontos de interseção da sua órbita com o plano da eclíptica (esses pontos são denominados nodos); a cada ano ocorrem no mínimo dois e no máximo sete eclipses.
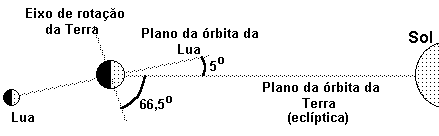
Figura 10 - Plano da órbita da Lua e a eclíptica.
A figura 11 explicita melhor as posições relativas Sol- Lua- Terra em cada uma das quatro fases principais. É importante destacar que, nas figuras deste trabalho, os diâmetros dos três corpos, bem como as distâncias entre seus centros, não estão representados em escala. Uma Nova ou uma Cheia ocorre quando, ignorando-se o fato de que o plano da órbita lunar não coincide com a eclíptica, os três corpos estão alinhados. A fase será Quarto Crescente ou Quarto Minguante quando o ângulo Sol- Lua- Terra for 90o.
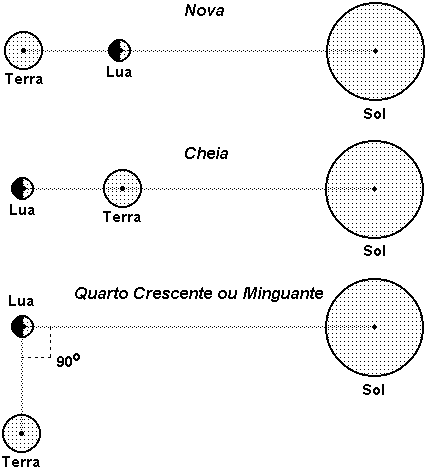
Figura 11 - Posição relativa Sol- Lua- Terra para as quatro fases principais da Lua.
Como na Lua Cheia e na Lua Nova o Sol e a Lua estão quase que alinhados com a Terra, as forças máximas de maré lunar e solar têm a mesma orientação, compondo uma força resultante máxima. Na Lua Quarto Crescente ou na Lua Quarto Minguante, as forças de maré solar e lunar parcialmente cancelam seus efeitos. A composição das forças de maré solar e lunar, em alguns pontos da Terra, estão representadas na figura 12.
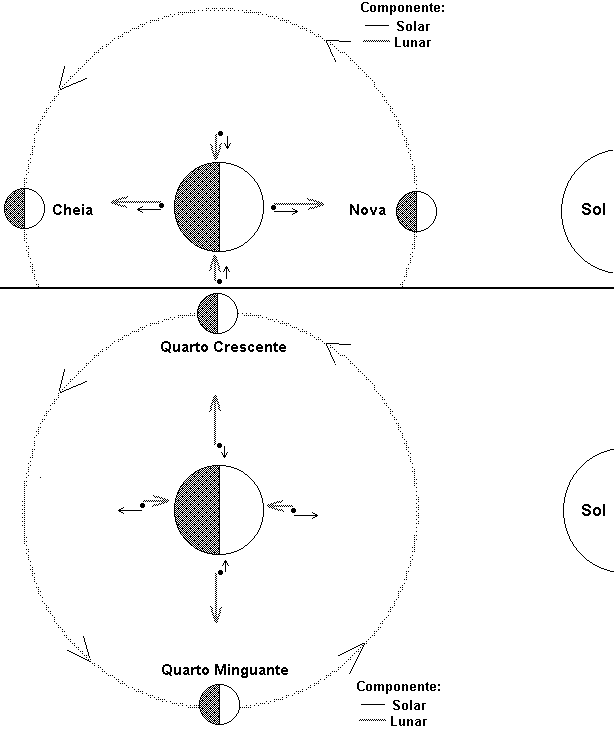
Figura 12 - Composição das forças de maré solar e lunar durante o mês lunar.
Na Lua Cheia ou na Lua Nova, quando as duas forças de maré concorrem para formar a resultante máxima, o valor máximo sobre um corpo de 1 kg na superfície da Terra é ![]() . É importante destacar que este valor representa uma parte em seis milhões da força gravitacional exercida pela Terra sobre esse corpo (seu peso). Ou seja, a força de maré é muito pequena, só produzindo efeitos facilmente notáveis em massas de água que se estendem por amplas regiões da Terra. O efeito médio sobre os oceanos é produzir um desnível de cerca de 1 m entre a maré alta e a maré baixa8. É importante notar que tal desnível é insignificante quando comparado ao raio da Terra.
. É importante destacar que este valor representa uma parte em seis milhões da força gravitacional exercida pela Terra sobre esse corpo (seu peso). Ou seja, a força de maré é muito pequena, só produzindo efeitos facilmente notáveis em massas de água que se estendem por amplas regiões da Terra. O efeito médio sobre os oceanos é produzir um desnível de cerca de 1 m entre a maré alta e a maré baixa8. É importante notar que tal desnível é insignificante quando comparado ao raio da Terra.
A figura 13 representa, de forma exagerada a deformação das águas oceânicas pelas forças de maré. Em primeira aproximação, pode-se admitir que as regiões de maré alta e maré baixa permanecem estacionadas enquanto a Terra gira. Uma estaca cravada na Terra passa ao longo do dia por duas regiões de maré alta e por duas regiões de maré baixa. Desta forma, em 24 h ocorrem duas marés altas e duas baixas.
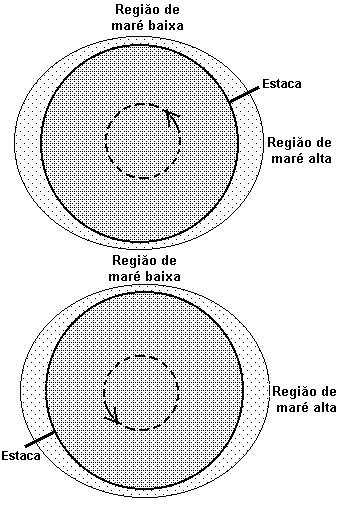
Figura 13 - Uma estaca cravada na Terra desloca-se através das regiões de maré alta e maré baixa.
Este modelo permite prever um intervalo de tempo de 12 h entre duas marés altas consecutivas. Todavia, a Lua se desloca em torno da Terra no mesmo sentido da rotação diária da Terra, arrastando consigo as deformações oceânicas, o intervalo de tempo entre duas marés altas consecutivas é maior do que 12 h; mais precisamente é de 12 h e 26 min.
3. - Relação das fases da Lua com o nascimento de bebês
Retomamos o argumento inicial da astróloga a favor da suposta influência da Lua sobre o nascimento de bebês e outras tantas crenças: "Se a Lua é capaz de agir nas enormes massas de água dos oceanos, como ela não teria efeito sobre os líquidos no útero da mãe ou sobre outros fluiídos corporais, influenciando no crescimento dos nossos cabelos?". Pelo exposto nas seções anteriores, compreendemos que os efeitos de maré somente ocorrem porque o campo gravitacional, que tanto a Lua quanto o Sol exercem sobre pontos diferentes da Terra, é variável em intensidade e orientação. Essa variação deve-se ao fato de que o raio da Terra não é desprezível frente às distâncias ao centro de qualquer um dos dois astros. As águas oceânicas, que se estendem por amplas regiões da Terra, acabam sofrendo diferentes atrações gravitacionais pela Lua ou pelo Sol, o que vem a ocasionar as marés. Mas não há efeito de maré em uma região com volume tão pequeno quanto o de uma bacia, de uma piscina ou até mesmo de um açude, pois distintos pontos dessas regiões estão praticamente eqüidistantes do astro atrator, sofrendo, como qualquer massa, uma força de maré, constante em todo o volume de líquido e, portanto, incapaz de deformá-lo. Da mesma forma, o líquido no útero da mãe (ou no bulbo capilar) não sofre efeitos de maré (deformações), ocorrendo apenas uma desprezível variação no seu peso aparente (não superior a uma parte em seis milhões). Adicionalmente, cabe notar que as maiores marés ocorrem em Lua Cheia e em Lua Nova, quando a Lua e o Sol estão quase alinhados com a Terra e a composição das duas forças de maré resulta ser máxima; na Lua Minguante ou Crescente as marés são menores. Entretanto, as marés acontecem em qualquer dia e não apenas nos dias das quatro fases principais da Lua. Conclui-se então que, se realmente nascessem mais bebês nos dias das quatro fases principais da Lua, tal fato não poderia ser atribuído aos efeitos de maré.
A fim de encontrar indícios a favor ou contra a tão difundida crença popular da existência de uma relação entre nascimentos de crianças e as fases da Lua, utilizamos dados dos arquivos sobre candidatos a concursos vestibulares da Universidade Federal do Rio Grande do Sul. A partir das datas de nascimento dos candidatos, e com auxílio de tabelas de lunação fornecidas pelo Observatório Nacional, determinamos em que dia do mês lunar cada candidato havia nascido. Um total de 93124 datas de nascimento constituem este estudo; 90% desses candidatos nasceram entre 1967 e 1983. Os restantes 10% nasceram entre 1930 e 1966.
O gráfico de barras da figura 14 representa o número de nascimentos nos dias das quatro fases principais da Lua (Nova, Crescente, Cheia e Minguante), bem como nos três dias imediatamente anteriores (-3, -2 e -1) e nos três dias imediatamente posteriores (+1, +2 e +3) a cada fase principal.
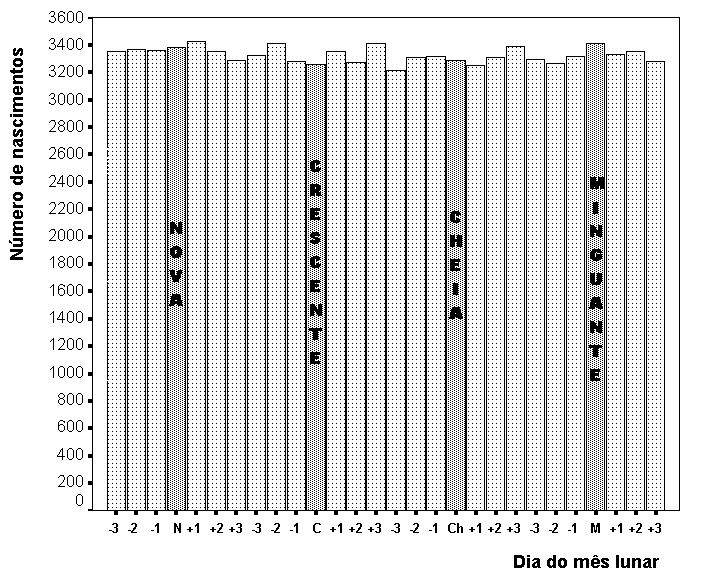
Figura 14 - Gráfico do número de nascimentos em função do dia do mês lunar.
Observa-se no gráfico que o número de nascimentos oscila em torno de 3300 por dia. O extremo superior no número de nascimentos ocorre no dia posterior à Lua Nova (3425 nascimentos); o inferior acontece três dias antes da Lua Cheia (3210 nascimentos). Um teste de significância estatística permite concluir que as diferenças no número de nascimentos ao longo do mês lunar estão dentro dos limites atribuíveis ao acaso (c 2 = 24,93; p = 0,579). Ou seja, não há nenhuma evidência nesses dados de que em algum dia especial do mês lunar nasça um número maior ou menor de bebês do que em qualquer outro, além das flutuações que podem ocorrer por mero acaso.
Pelo que foi exposto, o resultado do presente estudo contradiz a alegação que nos dias das quatro fases principais da Lua aumenta o número de nascimentos. Serão verdadeiras as outras tantas influências atribuídas à Lua pela sabedoria popular?
Agradecimentos. Agradeço aos colegas Profa. Maria Cristina Varriale, Prof. Rolando Axt e Prof. Paulo Mors a leitura atenta deste trabalho e as valiosas sugestões que permitiram melhorá-lo.
NOTAS
1 - Remonta ao século XVII a explicação dos mecanismos de maré pelo físico Isaac Newton (1643 - 1727).
2 - A Terra sofre ações por parte de qualquer corpo do sistema solar (e também age sobre qualquer um deles). São facilmente perceptíveis os efeitos de maré produzidos pelo Sol e pela Lua; a Lua apesar de ter massa muito menor que a do Sol, está muito mais próxima da Terra do que o Sol. Os efeitos de maré destes dois astros têm a mesma ordem de grandeza, o que se constitui em uma notável coincidência.
3 - O campo gravitacional pode ser descrito por um vetor: o vetor intensidade do campo gravitacional (![]() ). Este informa qual é a força gravitacional que atuaria sobre uma massa unitária localizada no ponto em questão; o seu módulo, no Sistema Internacional de unidades de medida, tem a dimensão de
). Este informa qual é a força gravitacional que atuaria sobre uma massa unitária localizada no ponto em questão; o seu módulo, no Sistema Internacional de unidades de medida, tem a dimensão de ![]() .
.
4 - A força gravitacional é igual ao produto da massa da partícula pela intensidade do campo gravitacional que sobre ela age, isto é, ![]() .
.
5 - O centro de massa do sistema Terra- Lua descreve uma volta em torno do Sol, em uma órbita aproximadamente circular, em um ano. A Terra descreve uma rotação completa em torno do seu próprio eixo em um dia. A Lua descreve uma rotação completa em torno de seu próprio eixo com exatamente o mesmo período da sua translação em torno do centro de massa do sistema Terra- Lua, isto é, em 27,3 dias. Esta sincronia dos dois movimentos da Lua, leva a que apresente sempre a mesma face para a Terra; foge do escopo deste trabalho dar uma justificativa pormenorizada para tal sincronia, entretanto, destacamos que em um passado distante ela não existia, vindo a ocorrer devido às forças de maré sobre a Lua.
6 - Não há nada de estranho nisto quando conhecemos as equações que permitem calcular as duas forças. Ambas as forças são diretamente proporcionais às massas dos dois astros; mas a força de atração gravitacional é inversamente proporcional ao quadrado da distância entre a Terra e cada um dos dois astros, enquanto a força de maré é inversamente proporcional ao cubo dessas distâncias. A massa do Sol é muito maior do que a Lua; todavia, ele também está muito mais distante da Terra do que a Lua. Desta forma, a força de maré dos dois astros acaba tendo a mesma ordem de grandeza; isto constitui-se em uma notável coincidência.
Qualitativamente, podemos dizer que a força de maré não depende do valor da força de atração, mas depende de quanto a força de atração varia ao longo do planeta (do gradiente da força de atração). O campo gravitacional da Lua sobre Terra, apesar de menos intenso do que o do Sol, é muito mais variável ao longo do planeta do que o do Sol
7 - Na verdade o eixo de rotação da Terra está inclinado cerca de 66,5o em relação ao plano de sua órbita em torno do Sol (eclíptica). Desta forma, a região da Terra vista na figura é em sua maior parte o hemisfério norte, mas também aparece uma pequena parcela do hemisfério sul.
8 - Em baías e estuários estreitos este efeito pode ser dramaticamente amplificado por diversos mecanismos, entre os quais a ressonância. A força de maré é uma força periódica com período de 12 h e 26 min, como veremos adiante. Caso o período do movimento natural das águas seja semelhante ao da força periódica, ocorre ressonância. Em alguns lugares a diferença de nível das águas entre a maré alta e baixa pode atingir cerca de 10m; na baía de Fundy (Nova Escócia) se registram as maiores marés, que atingem 15,3 m. Todavia, mesmo nestes casos extremos, isto representa uma deformação muitíssimo pequena se comparada ao raio da Terra.
![]()