6.6.2 Flujo y radiancia

Consideremos ahora un elemento de área dA orientado arbitrariamente en una región atravesada por radiación. Si es la intensidad específica monocromática en el punto donde se ubica dA y en la dirección q, entonces de acuerdo a la expresión (6.6), la cantidad representa físicamente la cantidad de energía que atraviesa dA por unidad de tiempo e intervalo de longitud de onda, en la particular dirección q, y dentro del ángulo sólido dw. Si se integra esta cantidad sobre todos los ángulos sólidos posibles, se obtendrá entonces la cantidad total de energía comprendida en el intervalo (l, l + dl), que atraviesa dA en la unidad de tiempo y en todas las direcciones posibles. Denotaremos con F_l este nuevo parámetro astrofísico y lo denominaremos densidad de flujo monocromático de radiación o simplemente flujo monocromático. Luego :

(6.14)

El flujo integrado será entonces :

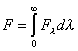(6.15)

Teniendo en cuenta la relación (6.10), el flujo anterior puede descomponerse de la siguiente manera :

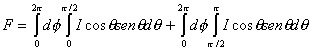(6.16)

Si se elige convenientemente el punto a partir del cual se mide el ángulo q, las dos integrales del segundo miembro pueden interpretarse como flujo saliente y entrante, respectivamente. Si se considera una estrella esférica y elegimos sobre su superficie un elemento de área normal al radio, el flujo entrante es nulo y la densidad de flujo de radiación resulta igual al flujo saliente. Por su parte, si consideramos un elemento de área en el interior de la estrella, F representará el flujo neto total, o bien el balance entre la radiación de todas las longitudes de onda que sale respecto de la que entra en el punto considerado.

Como es fácil imaginar, la densidad de flujo de radiación en cualquier punto de un campo isótropo es nula. Esta propiedad, usualmente conocida como segunda propiedad de un campo isótropo, resulta evidente de las expresiones (6.10) y (6.14). En efecto, de ambas expresiones se desprende que :

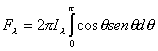, (6.17)

expresión ésta que se anula en cualquier punto del campo isótropo considerado al anularse la integral.

Otro parámetro astrofísico usado a menudo es la radiancia o emitencia de una fuente. Por definición, la radiancia monocromática L_l es la cantidad de energía por unidad de tiempo e intervalo de longitud de onda que atraviesa la unidad de área hacia todo un semiespacio. Es decir :

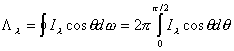(6.18)

La radiancia integrada será entonces :

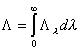(6.19)

Es evidente que en la superficie de una estrella, la radiancia y la densidad de flujo de radiación serán coincidentes. Para un campo isótropo existe una relación simple entre la radiancia y la intensidad específica. En efecto, de (6.17) se tiene :

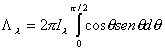(6.20)

La integral de la expresión anterior se resuelve de la siguiente manera :

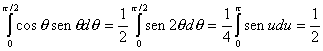
Luego: (6.21)

La expresión (6.21) representa la tercera propiedad de un campo de radiación isótropo.