6 CONCEPTOS BÁSICOS DE LA TEORÍA DE LA RADIACIÓN

 

Dado que el principal mecanismo de transporte de energía térmica en las atmósferas de la mayoría de las estrellas es el transporte radiativo, pasaremos a considerar los conceptos básicos de la teoría de la radiación térmica.

 

6.1 Intensidad específica monocromática e intensidad media

 

Comenzaremos definiendo la intensidad específica monocromática en un punto de un campo radiante y en una determinada dirección. Sea una superficie S arbitraria en un medio atravesado por radiación y consideremos en esa superficie un elemento de área dA (Figura 6-1). La energía con longitud de onda comprendida entre  y () que atraviesa el elemento de área dA,en la dirección, durante el tiempo dt, y se propaga dentro del ángulo sólido , es proporcional al área proyectada normalmente a la dirección de propagación, al ángulo sólido , al tiempo dt y al intervalo de longitud de onda  . Es decir :

 

 

 

                                             (6.6)

 

 

La función de proporcionalidad  en la expresión anterior es la intensidad específica monocromática en la dirección . El significado físico de  resulta evidente si se despeja esta cantidad en función de los restantes infinitésimos y se usa el concepto de límite :

 

 

 

                                                                                (6.7)

                                                    

                                                    

                                                     

                                                    

 

 

En el caso más general  es una función de la posición en el campo radiante considerado, de la dirección que se considere, de la longitud de onda  y del tiempo. Es decir,  se expresa de la siguiente manera :

 

                                             ,

 

 

en la cual x,y,z fijan la posición y () determinan la dirección considerada. Si se consideran estrellas estacionarias (invariables en el tiempo) con simetría esférica, la función  sólo dependerá del radio r, del ángulo  y de la longitud de onda .

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

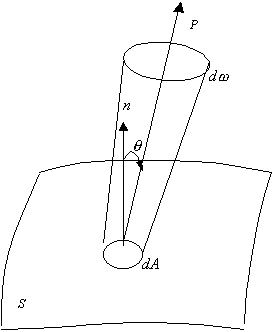
	Figura 6-1: Radiación comprendida en el intervalo l, l+dl que atraviesa el elemento de área dA en la dirección q, dentro del ángulo sólido dw y en el tiempo dt.

 

 

 

 

                                         

 

Si en un punto a una distancia r del centro de la estrella la intensidad específica monocromática en una cierta dirección es , la contribución de dicha intensidad en esa dirección y dentro de un ángulo sólido dw es . Si sumamos todas las posibles contribuciones  correspondientes a todas las direcciones y dividimos por el ángulo sólido correspondiente a todo el espacio, obtendremos para el punto del campo considerado un promedio de  con respecto a las direcciones. Denotaremos con  dicho promedio y lo denominaremos intensidad media monocromática en el punto considerado. Por consiguiente,  será :

 

 

 

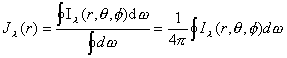                                                (6.8)

 

 

En la Figura 6-2 se ha esquematizado un punto a una distancia r del centro estelar y una dirección indicada por los ángulos  y f. Si existe simetría esférica, puede suprimirse la dependencia de  con el ángulo f. Además, cuando se considera una atmósfera estelar isótropa  no depende del ángulo. En consecuencia, de la expresión (6.8) resulta en forma inmediata la siguiente igualdad :

 

 

                                       ,                                                                (6.9)

 

 

en la cual hemos suprimido el subíndice r para mayor simplicidad. La expresión (6.9) es válida en cualquier punto de una atmósfera isótropa y se conoce como primera propiedad de un campo isótropo.

 

	Figura 6-2

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

                                              

 

La igualdad anterior puede también probarse de otra manera. En efecto, recordemos que un elemento diferencial de ángulo sólido se define como el cociente entre un elemento de superficie esférica dS subtendida a una distancia r y el cuadrado del radio r. Expresaremos ahora un elemento diferencial de ángulo sólido  en coordenadas esféricas. Para ello recurriremos a la Figura 6-3, en la cual se ha esquematizado un elemento de superficie esférica dS a una distancia r del centro de la esfera. El punto central del elemento de área esférico considerado está definido por las coordenadas esféricas (r, q,  f). De la Figura 6-3 se desprende que :

 

                                                       (6.10)

 

 

Por consiguiente, reemplazando (6.10) en (6.8) se tiene :

 

 

                                                                            (6.11)

 

 

 

  

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

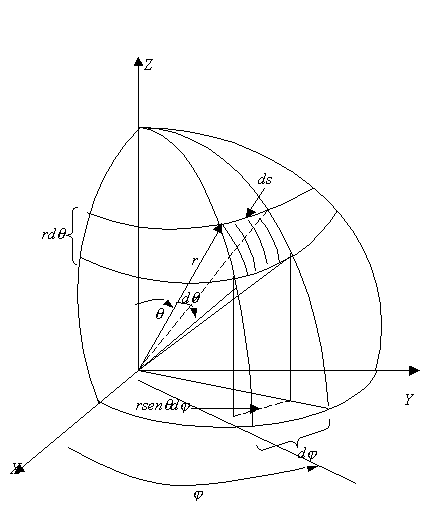
	Figura 6-3: Elemento de ángulo sólido en coordenadas esféricas

 

                                        

 

 

Si el campo radiativo es isótropo,  no depende del ángulo  y puede salir fuera de la integral en (6.11). En este caso, resulta en forma inmediata la igualdad (6.9).

 

En ocasiones, suele interesar la intensidad específica integrada sobre todas las longitudes de onda. Dicho parámetro se define como :

 

                                            

 

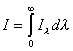
Una propiedad interesante de la intensidad específica monocromática es su invariancia respecto de la distancia. Esto significa que, en ausencia de fuentes y sumideros de energía, la intensidad específica monocromática  de un rayo de luz emitido por una fuente luminosa permanece invariable a cualquier distancia de la fuente.

 

Para mostrar esta propiedad consideremos un haz de rayos que atraviesa el área dA según la dirección q  y dentro del ángulo sólido dw (Figura 6.4). Si  es la intensidad específica monocromática en el punto P de dA y en la dirección q, la cantidad de energía dE_l  que emerge del elemento dA, en la dirección q, en el tiempo dt, dentro del ángulo sólido dw y cuyas longitudes de onda están comprendidas en el intervalo (l, l + dl), será :

 

 

                                             dE_l = I_l dA cosq dw dt dl                                    (6.12)

		Figura 6-4 : Invariancia de la intensidad específica

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

                                          

En la expresión anterior dw representa el ángulo sólido subtendido por el elemento de área dA’ a la distancia r. Luego, dw = dA’ cos q’ /r².

 

Por otra parte, la cantidad de energía  con longitudes de onda comprendidas en el intervalo  (l, l + dl) que atraviesa el elemento de área dA’ según la dirección q’, en el tiempo dt, dentro del ángulo sólido dw’, será :

 

 

                                              =  dA’ cos q’ dw’ dt dl ,                          (6.13)

 

 

en la cual dw’ = dA cosq/r² e  es la intensidad específica monocromática en el punto P’ de dA’ y en la dirección q’.

 

Si entre dA y dA’ no existen fuentes ni sumideros de energía, a medida que estos elementos de área tienden a cero, las cantidades dE_l y  deben tender a igualarse. En este caso, resulta inmediatamente la igualdad  = .