8 INTERACCIÓN
ENTRE LA MATERIA Y LA RADIACIÓN :
COEFICIENTES DE ABSORCIÓN Y EMISIÓN
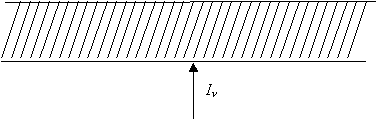
Si sobre una capa de material de cualquier naturaleza y espesor dz incide radiación de intensidad In normalmente a dicha capa, la experiencia indica que la cantidad dIn de radiación absorbida en la
capa es proporcional a su espesor y a la intensidad In de la radiación incidente (Figura
6-8) :
(6.43)
El coeficiente de proporcionalidad 
es, por definición,
el coeficiente de absorción por
unidad de longitud. El signo menos en la expresión anterior indica que se trata de una absorción, esto es, el
incremento dIn debe ser negativo. El coeficiente 
suele escribirse como
el producto de la densidad de materia r y el coeficiente másico de absorción kn :
n (6.44)
z + dz
z
Figura 6-8 : Capa plano paralela de espesor dz atravesada por radiación
En el sistema c.g.s. el coeficiente 
tiene unidades de cm-1, en tanto que r se
mide en gr cm-3. En
consecuencia, en ese mismo sistema el coeficiente kn deberá tener unidades de cm2
gr-1. De allí que kn es un coeficiente de
absorción por unidad de masa. En
adelante llamaremos a kn simplemente coeficiente de absorción. La ecuación diferencial (6.43) puede ahora escribirse de
la siguiente manera :
dIn
= - knr In dz (6.45)
Dos procesos físicos contribuyen al valor numérico del coeficiente
de absorción. En efecto, la intensidad puede perderse por absorción verdadera, o bien por dispersión
de la radiación. En el primer caso, los fotones al ser absorbidos desaparecen y
aumenta la energía cinética de los átomos (energía térmica). Naturalmente que
la energía de los fotones absorbidos debe ser luego reemitida en alguna dirección.
En el proceso de dispersión, por el contrario, los fotones no son absorbidos
sino desviados hacia otros ángulos diferentes de aquéllos que traían
originalmente. El resultado neto del proceso de dispersión de fotones es una absorción aparente. Recordemos, por
ejemplo, que la dispersión en la atmósfera terrestre producida por partículas
tales como átomos o moléculas, es mayor cuanto mayor es la frecuencia.
Análogamente, la dispersión de la radiación producida por átomos y/o moléculas
en una capa de una atmósfera estelar va a contribuir en forma diferente al
coeficiente de absorción, dependiendo de la frecuencia.
La ecuación diferencial (6.45) indica la atenuación relativa que
sufre un rayo luminoso al atravesar una capa de espesor dz. Si se integra esta ecuación entre los límites z1 y z2 y denotamos con 
e 
a las intensidades
específicas correspondientes, se tiene :
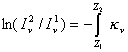
O bien :
(6.46)
Por lo tanto, la intensidad 
que emerge normalmente
de la capa de espesor (z2 – z1)
es la intensidad I
que entró, correspondientemente atenuada por la
exponencial de (6.46). Hemos pues obtenido la conocida ley de extinción.
Podríamos ahora preguntarnos cuál es la intensidad específica que llega a la superficie de una estrella siguiendo la dirección del radio, proveniente de una profundidad geométrica x de la atmósfera de la misma ? La profundidad geométrica x se mide en la dirección del radio estelar y por convención la consideraremos nula en la superficie de la estrella y aumentando desde el centro hacia afuera por valores negativos. De acuerdo a la (6.46), se tiene :
(6.47)
Introduciremos ahora una cantidad adimensional denominada profundidad óptica, definida de la
siguiente manera :
dtn =
- knr dx
(6.48)
De la definición anterior se desprende que las profundidades óptica
y geométrica crecen según la misma dirección pero en sentido opuesto. Al igual
que antes, adoptaremos tn = 0 en la superficie estelar. Si integramos (6.48) entre un punto a
profundidad óptica tn y la superficie estelar, resulta :
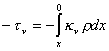(6.49)
Luego, de (6.47) y (6.49) la intensidad específica monocromática que
alcanza la superficie estelar (tn = 0) proveniente de una capa a profundidad óptica tn será :
(6.50)
Se aprecia ahora con claridad el significado físico de la profundidad óptica. En efecto, de (6.50) vemos que dicha profundidad determina la fracción de intensidad específica monocromática proveniente de una capa que alcanza efectivamente la superficie, incidiendo normalmente sobre la misma. De una capa a profunidad óptica tn = 0.1, por ejemplo, dado que e-0.1 = 0.90, llegará a la superficie el 90% de la radiación. Por su parte, de capas ubicadas a profundidades ópticas de 1, 2 y 3, por ejemplo, llegará el 37%, 14% y 5%, respectivamente. A los fines prácticos, es muchas veces razonable adoptar como fotosfera efectiva de una estrella el conjunto de capas ubicadas a profundidades ópticas menores o iguales que tn = 3.
Consideremos ahora el proceso de emisión de energía en la atmósfera
de una estrella. Se define el coeficiente de emisión por unidad de volumen en admitiendo que la cantidad de energía dE(n)em emitida por un elemento
de volumen dV, en el tiempo dt, dentro del rango (n,n+dn) y
dentro de un ángulo sólido dw,
debe aumentar proporcionalmente con el elemento de volumen, el tiempo, el rango
de frecuencias y el ángulo sólido considerados. El coeficiente de
proporcionalidad entre dE(n)em y los restantes diferenciales es, por definición, el coeficiente de emisión por unidad de volumen.
Luego :
dE(n)em = en dV dn dt dw (6.51)
Si In(q) es la intensidad específica en el punto del campo radiante
considerado y en la dirección de propagación q, cuál será la contribución dIn(em) a dicha intensidad,
debida a la energía emitida en ese punto por el elemento de volumen en la
dirección considerada ? Para responder a esta pregunta consideremos que el
elemento de volumen dV es un cilindro
de base dA y altura dx (Figura
6-9), de modo que la contribución del cilindro dV a la energía emitida en ese punto y en la dirección considerada
es : en dA
dx dn dw dt. Si en lugar de dx en la expresión anterior incluimos ds.cosq, siendo ds un elemento de
trayectoria en la dirección de propagación (Figura
6-9), la contribución del elemento dV
a la energía emitida en la dirección de propagación será :
dE(n)em = en ds dA cosq dn dw dt (6.52)
Comparando (6.52) con la definición de intensidad específica, se
desprende que el producto (en ds) representa la contribución del volumen dV a la intensidad específica monocromática en la dirección
considerada. Denotando dicha contribución con dIn(em), se tiene :
dIn(em) = ends (6.53)
En general, la contribución de cualquier volumen elemental a la intensidad específica en una cierta dirección de propagación, es igual al coeficiente de emisión por unidad de volumen multiplicado por el tamaño del elemento de volumen en la dirección de propagación.
El coeficiente de emisión puede también ser definido por unidad de masa. Si dm representa el elemento de masa existente dentro del volumen elemental dV, debe entonces verificarse que :
en dV = jn dm , (6.54)
en la cual jn es el coeficiente de emisión por unidad de masa. De (6.54) resulta
simplemente que en =
jnr,
siendo r la densidad. Por consiguiente, la expresión (6.53) puede también
escribirse de la siguiente manera :
dIn(em) = jnr ds (6.55)
Es decir, el incremento de la intensidad específica dIn producido por una masa de
densidad r que emite en la dirección ds
es simplemente jnrds. Si comparamos las expresiones (6.55) y (6.45) notamos que el
coeficiente de emisión por unidad de masa jn se define de una manera comparativamente similar al coeficiente de
absorción por unidad de masa kn.
De la misma manera que el coeficiente de absorción kn debe incluir todos los
efectos que quitan energía de un haz de radiación, el coeficiente de emisión jn deberá tener en cuenta todos
los procesos que agregan energía a dicho haz. A la emisión de radiación en una
cierta dirección contribuyen básicamente dos procesos: la emisión real de fotones
creados por la materia (emisión térmica) y la emisión aparente debida a los
fotones dispersados en la dirección considerada.
Nótese de (6.55) que si r está dada en gr cm-3
y ds en cm, las unidades del coeficiente
jn son las unidades de In multiplicadas por cm2
gr-1.
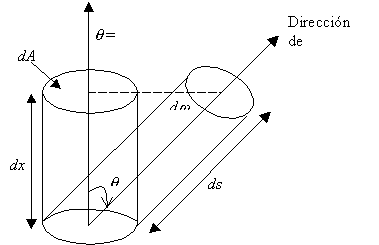
Figura
6-9 : Elemento de volumen utilizado para
definir el coeficiente de emisión
