EL COEFICIENTE DE ABSORCIÓN CONTINUA

10.1 INTRODUCCIÓN

En la Sección 6.8 hemos definido el coeficiente másico de absorción k_n. Por lo general, suelen definirse dos coeficientes de absorción, uno que da lugar al espectro continuo, usualmente denotado k_n, y otro que sólo tiene validez en las líneas espectrales y suele denotarse l_n. Nuestro problema consiste ahora en calcular el coeficiente másico de absorción continua k_n , con la mejor precisión posible. Si, como hemos visto en el capítulo anterior, no es posible definir un coeficiente de absorción continua independiente de la frecuencia, habrá entonces que calcular la dependencia explícita con esta variable. Resulta fácil imaginar que la forma del espectro continuo de una estrella, estará estrechamente ligada a la dependencia del coeficiente de absorción con la frecuencia.

10.2 ORIGEN DE LA OPACIDAD CONTINUA : TRANSICIONES LIGADO-LIBRE Y LIBRE-LIBRE

¿ Cuál es el orígen de la opacidad continua ? Es decir, a qué se debe la absorción continua observada en los espectros estelares ? En rigor, la absorción continua observada en una determinada frecuencia en un espectro estelar, resulta de la suma de las absorciones (verdaderas y aparentes) producidas en esa frecuencia por determinados procesos físicos, los cuales involucran distintos elementos químicos en sus respectivos estados de excitación y/o ionización. Como veremos en este capítulo, las absorciones deben ser corregidas o disminuidas por las denominadas absorciones negativas o emisiones estimuladas.

Los procesos físicos de absorción verdadera que contribuyen a la opacidad continua pueden ser divididos esencialmente en dos categorías: (1) procesos de absorción ligado-libre y (2) procesos libre-libre. Los mecanismos de absorción aparente incluyen básicamente la dispersión de la radiación producida por electrones libres (dispersión Thompson) o bien por sistemas ligados, tales como átomos o moléculas (dispersión Rayleigh).

En un proceso de absorción radiativo ligado-libre (ionización), un átomo absorbe un fotón hn del campo de radiación, cuya energía es suficientemente grande como para liberar un electrón, quedando en consecuencia ionizado el átomo. El proceso de absorción en este caso es radiativo porque involucra fotones y es ligado-libre simplemente porque el electrón que estaba ligado al átomo, se liberó de él. Puesto que las posibles energías hn que pueden ser absorbidas mediante este proceso son infinitas y varían con continuidad a partir de una energía umbral (energía mínima necesaria para arrancar un electrón), las transiciones radiativas ligado-libre de un determinado elemento químico contribuyen al espectro continuo observado. Precisamente, el espectro de ionizaciones es el espectro continuo debido a transiciones radiativas ligado-libre. Nótese que los procesos inversos a las fotoionizaciones corresponden a las transiciones libre-ligado, usualmente llamadas recombinaciones.

Un proceso de absorción libre-libre ocurre cuando una partícula libre (un electrón, por ejemplo), moviéndose en el campo de un protón - puede ser en general un ión o un átomo neutro - absorbe un fotón de energía hn y éste desaparece. Como resultado de la absorción, la partícula libre (electrón) cambia su velocidad pasando de su órbita hiperbólica original a otra algo más alejada del protón (Figura 10-1). La transición es radiativa porque implica la desaparición de un fotón. Es además libre-libre porque el electrón que estaba libre (energía positiva) continúa con energía positiva. Nuevamente, dado que las posibles energías hn que pueden ser absorbidas mediante este proceso son infinitas y varían con continuidad, las transiciones radiativas libre-libre de un determinado elemento químico contribuyen al espectro continuo.

Figura 10-1 : En un proceso de absorción radiativa libre-libre, un electrón moviéndose en el campo de un protón absorbe un fotón y cambia su órbita hiperbólica original hacia otra más alejada del protón.

Cuando se menciona la contribución de los procesos libre-libre de un determinado elemento químico a la opacidad del continuo, se hace referencia a la capacidad que tienen los electrones libres de dicho elemento para absorber energía por procesos libre-libre tales como el mencionado.

El conocido efecto Compton no puede considerarse propiamente un ejemplo de proceso de absorción libre-libre. Ello se debe a que este efecto consiste en la interacción de un fotón con un electrón en la manera esquematizada en la Figura 10-2. Es decir, incide un fotón de energía hn sobre el electrón y una parte de la energía del fotón es absorbida por el electrón, el cual adquiere una cierta velocidad o la aumenta si es que se encontraba inicialmente en reposo. Como resultado de la interacción, el fotón inicial hn se transforma en otro hn’ de menor energía, habiendo el electrón absorbido en el proceso la cantidad DE = h(n - n’). Dado que el fotón no desaparece sino que se enrojece, no corresponde hablar propiamente de absorción. Además, para que ocurra una transición libre-libre no puede haber un electrón libre en el espacio, sino que el electrón debe estar en el campo de un átomo o ión, es decir, debe tener un núcleo asociado.

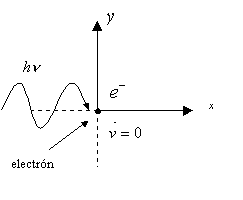
Figura 10-2 : Al chocar un fotón hn con un electrón en reposo, el fotón se dispersa en la dirección del ángulo j, con una frecuencia n’ menor que la original, en tanto que el electrón adquiere una velocidad v y se dispersa en la dirección q.

Una transición ligado-libre puede ocurrir no sólo radiativamente involucrando fotones, sino también colisionalmente. En este último caso no desaparece ningún fotón del campo radiante. En efecto, un proceso de absorción colisional ligado-libre ocurre cuando una partícula libre (electrón, por ejemplo), moviéndose con una velocidad v_i elevada, colisiona con un átomo o ión. Si dicha partícula tiene una elevada energía cinética en virtud de su alta velocidad, al colisionar con el átomo o ión puede cederle parte de su energía cinética, desviarse su trayectoria y continuar con una velocidad final v_f, siendo v_f < v_i. Si la energía DE = cedida por la partícula al átomo o ión es suficientemente grande como para producir el desprendimiento de un electrón, entonces el átomo o ión absorbió colisionalmente la energía DE. El proceso es ligado-libre debido a que el electrón que estaba ligado al átomo o ión quedó liberado, esto es, su energía pasó de un valor negativo a otro positivo. Sin embargo, en virtud de que las transiciones colisionales ligado-libre de un determinado elemento químico no implican la desaparición de fotones, estos procesos no contribuyen al espectro continuo.

También pueden ocurrir procesos libre-libre de tipo colisional, los cuales tampoco involucran fotones. Como resultado de un proceso de este tipo, una partícula puede ganar (absorber) o perder energía cinética. Sin embargo, dado que este proceso no implica la desaparición de fotón alguno, no contribuye al espectro continuo. Un ejemplo de absorción colisional libre-libre lo constituye la colisión de un electrón de velocidad v_i con otra partícula cualquiera (átomo, ión, electrón, etc). Si como resultado de la colisión el electrón adquiere una velocidad v_f mayor que la velocidad v_i que traía inicialmente, significa que la partícula entregó parte de su energía cinética al electrón y éste la absorbió. Colisión no significa literalmente choque, aunque efectivamente éste puede ocurrir, sino más bien interacción debido a un pasaje cercano.

Cuando un electrón, después de colisionar con otra partícula (un protón, por ejemplo), pierde parte de su energía siendo la misma emitida, se dice que ocurrió también una transición libre-libre. La energía emitida en este caso se denomina radiación de frenado (bremsstrahlung) debido a que el electrón se frena en parte al emitir.

Finalmente, debemos mencionar que existen también las transiciones ligado-ligado, las cuales contribuyen a la formación de las líneas espectrales y no al espectro continuo. Si bien la absorción en las líneas no se incluye en el coeficiente k_n, cuando en ciertas regiones del espectro muchas líneas se superponen (blends), éstas se comportan como si contribuyeran a la absorción continua. La disminución del continuo debido a la superposición de líneas en una determinada región del espectro se conoce como efecto blanketing o efecto frazada.

10.3 COMPOSICIÓN QUÍMICA EN LAS FOTOSFERAS ESTELARES

Para determinar el coeficiente de absorción continua total de una fotosfera estelar, es necesario conocer al menos en forma aproximada la composición química de la misma. Esto es así simplemente porque la capacidad de absorción varía para cada elemento químico. El coeficiente de absorción total determinado por la composición química de toda la fotosfera, dependerá marcadamente de las cantidades relativas de los elementos químicos presentes en la misma.

Las observaciones demuestran que la composición química de las fotosferas estelares es aproximadamente similar en la gran mayoría de las estrellas. En efecto, suponiendo la composición química constante y admitiendo que sólo cambia la temperatura y la presión electrónica, es posible explicar en forma completa la secuencia espectral de Harvard, incluyendo las distintas clases de luminosidad .

Dado que en cada fotosfera la densidad suele ser por lo general diferente, es razonable hablar de composiciones químicas relativas o de porcentajes presentes de cada elemento químico. Esta composición química relativa puede definirse tomando la cantidad de algún elemento como unidad y luego refiriendo los otros elementos a éste, o bien considerando el conjunto de todos los elementos como el 100% y luego indicando el porcentaje de cada elemento presente en la fotosfera. A su vez, la cantidad relativa de cada elemento puede expresarse por número de átomos o por masa. En el primer caso, si en un centímetro cúbico de la fotosfera de una estrella hay n₁ átomos del elemento 1, n₂ átomos del elemento 2, etc, y tomamos como unidad la cantidad de átomos del elemento 1, entonces la cantidad relativa del elemento j (por número de átomos) será :

(10.1)

Por su parte, si la masa de un átomo del elemento 1 es m₁, la masa de un átomo del elemento 2 es m₂, etc., y tomamos como unidad la masa total de los átomos del elemento 1, la cantidad relativa del elemento j (por masa) será :

(10.2)

Análogamente, la cantidad relativa del elemento j expresada como un porcentaje respecto del total y por número de átomos será :

, (10.3)

en tanto que la cantidad relativa del elemento j expresada como un porcentaje respecto del total y por masa será :

(10.4)

Si bien las cantidades relativas de los diversos elementos químicos varían en función de la profundidad óptica en cada fotosfera estelar, numerosas observaciones sugieren que esta variación no es significativa, motivo por el cual aceptaremos en adelante que al especificar la composición química relativa, en cualquiera de las formas antes mencionadas, los coeficientes respectivos ( o ) son los mismos en toda la fotosfera estelar. Numerosas observaciones demuestran además que el hidrógeno es el elemento preponderante no sólo en las estrellas, sino también en las nebulosas planetarias y en general en el medio interestelar. En particular, por ser este elemento el más abundante en las fotosferas estelares, su contribución al coeficiente de absorción continua será fundamental.

10.4 UNIDADES DEL COEFICIENTE DE ABSORCIÓN CONTINUA

Si bien mantendremos la notación k_n previamente introducida para el coeficiente másico de absorción continua, expresado en cm² por gramo de materia estelar en el sistema c.g.s., denotaremos en adelante con la letra a al coeficiente de absorción continua expresado en cm² por absorbedor. En consecuencia, cada elemento químico estará caracterizado por un determinado valor de a. En este contexto, dos átomos de un mismo elemento químico en distintos estados de excitación, por ejemplo, serán considerados dos absorbedores diferentes, cada uno de los cuales estará caracterizado por un determinado valor del coeficiente a. Nótese que este coeficiente a dependerá en general de la longitud de onda l o frecuencia n que se considere. Sin embargo, dado que a_l o a_n no representan una función de distribución en el mismo sentido que o , por ejemplo, no usaremos en adelante el subíndice. Esto significa que una vez fijada l o n, el coeficiente será simplemente un número.

Llamaremos además k al coeficiente de absorción continua de un elemento químico, cuando el mismo esté expresado en cm² por átomo de hidrógeno neutro. Al igual que a, el coeficiente k presentará una dependencia con la longitud de onda, pero no representa una función de distribución. Finalmente, el producto es el coeficiente de absorción continua por unidad de longitud.

10.5 COEFICIENTE DE ABSORCIÓN CONTINUA EN FUNCIÓN DE LOS COEFICIENTES DE EINSTEIN

En la Sección 3.15 hemos descripto tres clases de transiciones radiativas posibles denominadas, respectivamente, emisión espontánea, absorción verdadera y emisión estimulada. La frecuencia con que se producen estos diferentes procesos depende de la población de los niveles de energía correspondientes, de las denominadas probabilidades de transición de dichos niveles y, en los casos de la absorción y la emisión estimulada, de la intensidad del campo de radiación.

Consideremos ahora sólo dos niveles de energía i y j de un átomo y sea E = hn la diferencia de energía entre los mismos, siendo i el nivel superior y j el inferior. Supongamos que el átomo en cuestión se encuentra en un campo de radiación isótropo y veamos cuáles son las transiciones posibles entre los dos niveles considerados.

La probabilidad de que el átomo emita espontáneamente, sin influencia del campo, su energía cuántica hn en un tiempo dt y que ese fotón siga su camino dentro de un ángulo sólido dw es :

, (10.5)

en la cual se denomina coeficiente de Einstein de emisión espontánea o probabilidad de transición espontánea. Este coeficiente expresa entonces la probabilidad de que el átomo emita espontáneamente su energía hn en el tiempo dt y dentro del ángulo sólido dw. El coeficiente depende de los dos niveles involucrados, de modo que para cada par de niveles de energía de un átomo es un número, una constante. Si átomos por unidad de volumen se encuentran en el nivel i, la contribución de la emisión espontánea al coeficiente de emisión total por unidad de volumen es :

(10.6)

Si el átomo se encuentra en un campo radiante isótropo, el cual dispone de fotones con energía hn, dicho campo puede estimular o inducir al átomo en el nivel i a emitir un fotón hn. Este proceso de emisión estimulada o inducida se conoce también como absorción negativa, ya que representa el proceso inverso de la absorción de un fotón del campo. En la emisión estimulada o absorción negativa, el fotón es emitido en la misma dirección y fase que el fotón incidente. Es decir, los fotones en este caso no son emitidos en direcciones al azar como ocurre en el proceso de emisión espontánea.

La probabilidad de que un átomo sea inducido por el campo a emitir su energía hn en un tiempo dt y dentro de un ángulo sólido dw es :

, (10.7)

en la cual se denomina coeficiente de Einstein de emisión estimulada. Dado que la emisión estimulada representa como hemos dicho una absorción negativa, de acuerdo a (6.45) la cantidad de energía absorbida negativamente por unidad de longitud es :

(10.8)

Finalmente, la probabilidad de que sea absorbido realmente un cuanto de energía hn del campo y que el átomo se excite del nivel j al i, en un tiempo dt y dentro de un ángulo sólido dw, es :

, (10.9)

en la cual es el coeficiente de Einstein de absorción verdadera. Teniendo en cuenta la expresión (6.45), la radiación absorbida verdaderamente por unidad de longitud, en la unidad de tiempo, será :

, (10.10)

siendo el número de átomos en el nivel j por unidad de volumen.

En consecuencia, la radiación total absorbida por unidad de longitud de camino del rayo de intensidad es :

, (10.11)

O bien :

, (10.12)

en la cual k_n queda expresado en función de los coeficientes de Einstein.

10.6 FACTOR DE EMISIONES ESTIMULADAS

De acuerdo a lo expresado en la sección precedente, el número de emisiones espontáneas del nivel i al j por unidad de tiempo, unidad de ángulo sólido y unidad de volumen es , en tanto que y representan respectivamente los números de absorciones negativas y absorciones verdaderas, por segundo, unidad de ángulo sólido y unidad de volumen. Si suponemos que estamos en condiciones de equilibrio térmico, las poblaciones relativas de los dos niveles de energía considerados verifican la ley de Boltzmann :

, (10.13)

en la cual T es la temperatura, y los pesos estadísticos de los respectivos niveles y hn la diferencia de energía entre los 2 niveles. En equilibrio térmico existe balance detallado de energía, de manera que el número total de emisiones debe igualar el número de absorciones. Esto es :

, (10.14)

en la cual hemos usado en lugar de porque en condiciones de equilibrio térmico la intensidad está dada por la función de Planck. De (10.13) y (10.14) resulta :

,

o bien, multiplicando por y ordenando términos, se tiene :

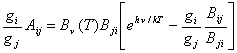(10.15)

Reemplazando en (10.15) la función de Planck dada en (2.8) se obtiene :

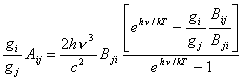(10.16)

Dado que los 3 coeficientes de Einstein que aparecen en esta última expresion no pueden depender de la temperatura T, ya que son constantes para un determinado átomo, deben entonces verificarse las siguientes igualdades :

(10.17)

y

(10.18)

Nótese que si uno de los coeficientes de Einstein se conoce, pueden derivarse los otros dos de las expresiones anteriores. Por otra parte, si bien las relaciones entre los coeficientes de Einstein han sido derivadas considerando condiciones de equilibrio térmico, es importante destacar que las expresiones (10.17) y (10.18) se mantienen en todas las condiciones.

El problema que nos planteamos en este capítulo es obtener el coeficiente másico de absorción continua k_n y hemos visto en la sección precedente que las emisiones estimuladas o absorciones negativas tienen su influencia en la absorción total. Si se escribe (10.12) de la siguiente manera :

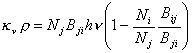, (10.19)

y se tienen en cuenta (10.13) y (10.17) resulta :

(10.20)

El término entre paréntesis en la expresión anterior tiene en cuenta las emisiones estimuladas, ya que es pura absorción. En rigor, lo que representa absorción verdadera es el producto . Sin embargo, si se multiplica miembro a miembro la expresión (10.20) por , el factor entre paréntesis representa las emisiones estimuladas. En otras palabras, la absorción verdadera producida es disminuida en un factor , conocido como factor de emisiones estimuladas, el cual aumenta a medida que aumenta la temperatura y a medida que disminuye la frecuencia considerada. Para una estrella A0V, por ejemplo, cuya temperatura superficial es del orden de 10.000 ^oK, la disminución de la absorción debida al factor de emisiones estimuladas supera el 20% en la región del continuo de Paschen y más allá de 10.000 Å sobrepasa el 30%.

Debe tenerse en cuenta que el factor de emisiones estimuladas ha sido derivado para el caso de una transición ligado-ligado. Milne (1924), sin embargo, ha mostrado que dicho factor se mantiene para el caso de una transición libre-libre.

10.7 CONTRIBUCIÓN DEL HIDRÓGENO NEUTRO A LA OPACIDAD

CONTINUA

10.7.1 Procesos ligado-libre

Cada elemento químico contribuye en forma particular al coeficiente de absorción continua. Dado que el hidrógeno es el elemento más abundante en las fotosferas de las estrellas normales, comenzaremos examinando la contribución a la opacidad continua de este elemento. Los procesos que aportan al coeficiente de absorción continua son las transiciones ligado-libre y libre-libre del mencionado elemento.

Comencemos por considerar las transiciones radiativas ligado-libre del hidrógeno neutro. Para que dichas transiciones puedan ocurrir es necesario proporcionar al átomo una energía hn suficientemente grande como para liberarlo de su único electrón. Si R = es la constante de Rydberg, de (3.17) se desprende que la energía del nivel discreto con número cuántico principal n, ligado al átomo de hidrógeno (Z = 1), es . Si un electrón en ese nivel absorbe un fotón de energía hn y se libera del átomo con una velocidad v, resulta :

, (10.21)

en la cual el primer miembro es la energía cinética del electrón y R = 1.0968x10⁵ cm^-1 para el átomo de hidrógeno.

En la Sección 3.4 vimos que el potencial de ionización del hidrógeno neutro es 13.6 eV. Ésta es la energía mínima necesaria para arrancarle al átomo su único electrón desde el nivel fundamental. En otras palabras, el potencial de ionización del hidrógeno neutro es la energía que es necesario suministrar al átomo para arrancarle su único electrón desde el nivel fundamental y de manera tal que dicho electrón se libere con energía cinética nula. De (10.21) se deduce que I = hRc, cantidad ésta que para el átomo de H equivale a 13.6 eV. Por consiguiente, sólo aquellos fotones con energías mayores que 13.6 eV estarán en condiciones de producir transiciones radiativas ligado-libre desde el nivel fundamental del átomo de H. Dado que la longitud de onda asociada a un fotón con esta energía es l_L = hc/13.6 eV = 912 Å, todos los fotones con energías mayores que 13.6 eV, o bien con longitudes de onda asociadas menores que 912 Å, estarán en condiciones de fotoionizar al hidrógeno desde el nivel fundamental. Esta l_{L =} 912 Å representa el límite de la serie de Lyman.

De (10.21) se desprende además que para ionizar el átomo de H desde el nivel n = 2 se requiere una energía hn = I/4 = 3.40 eV. La longitud de onda asociada a esta energía es ahora l_B = hc/3.40 eV = 3647 Å (límite de la serie de Balmer), de manera que todos los fotones con l £ l_B tendrán energías suficientes como para producir transiciones radiativas ligado-libre del átomo de H neutro desde el segundo nivel (n = 2) y asi sucesivamente para las diferentes series espectrales. Los límites de las series de Paschen, Brackett y Pfund corresponden a las longitudes de onda 8206 Å, 14588 Å y 22790 Å, respectivamente.

Nuestro problema consiste en obtener una expresión del coeficiente a en cm² por absorbedor, para el H neutro. Kramers (1923) consideró un átomo hidrogénico con un electrón moviéndose en el campo de la carga Ze, en una órbita cuyo número cuántico principal es n. Haciendo uso de la Física Clásica y para el caso Z = 1, el mencionado autor obtuvo una expresión para el coeficiente . Gaunt (1930) modificó levemente la derivación de Kramers usando la Mecánica Cuántica y obtuvo :

, (10.22)

en la cual e = 4.803x10^-10 u.e. es la carga del electrón y un factor de corrección, conocido como factor de Gaunt para las transiciones ligado-libre, el cual hace coincidir la expresión de Kramers obtenida a partir de la Física Clásica, con los resultados rigurosos obtenidos a partir de la Mecánica Cuántica. La (10.22) se conoce como fórmula de Kramers-Gaunt.

En términos de la longitud de onda la expresión anterior puede escribirse como :

, (10.23)

o bien en forma simplificada :

, (10.24)

siendo 1.044x10^-26 y estando l expresada en angstroms.

El factor de Gaunt depende básicamente de n y de l, en general difiere poco de la unidad y, de acuerdo a Menzel y Pekeris (1935), puede calcularse de la expresión :

(10.25)

Nótese de (10.24) que, dentro de cada banda de absorción (fijado n), el coeficiente a_n aumenta proporcionalmente con la tercera potencia de la longitud de onda. Asimismo, para una determinada longitud de onda, el coeficiente de absorción decrece proporcionalmente a 1/n⁵. Esto significa que el coeficiente de absorción de un átomo de H altamente excitado es considerablemente menor que el de otro levemente excitado. Como el número de órbitas en el átomo de H es infinito, el número de las bandas de absorción también es infinito y cada una de ellas contribuirá a la absorción en una determinada longitud de onda. Las bandas con n = 1, 2, 3, ..., ¥ corresponden a la fotoionización del átomo de H desde los niveles 1, 2, 3, ..., ¥.

En las frecuencias correspondientes a los límites de ionización, donde la energía cinética del electrón liberado se anula, la ecuación (10.21) implica :

, (10.26)

en la cual representa la frecuencia correspondiente al límite de ionización. Dado que , de (10.24) y (10.26) resulta :

, (10.27)

en la cual representa el valor del coeficiente correspondiente al límite de ionización. La (10.27) muestra que aumenta proporcionalmente con n.

La Figura 10-3 ilustra la variación del coeficiente en términos de la longitud de onda. Las unidades se han elegido de tal manera que = 1 en l = 100 Å y n = 1. Hay pues una curva para cada n y a su vez cada una de estas curvas aumenta con el cubo de la longitud de onda según expresa (10.24). Además, las ordenadas correspondientes a los extremos de cada curva aumentan en forma proporcional a n según indica (10.27). Sólo se ilustran en la figura las curvas correspondientes a los primeros 4 niveles y parte del coeficiente de absorción correspondiente a n = 5. La influencia de los factores de Gaunt no ha sido considerada en la figura. Si se desea conocer el coeficiente de absorción del H neutro en una determinada longitud de onda, 6000 Å por ejemplo, deben sumarse las contribuciones correspondientes a n = 1, n = 2, n = 3, etc. En este caso particular, sin embargo, la contribución n = 6 y restantes resultan prácticamente despreciables, en tanto que las correspondientes a n = 1 y n = 2 son nulas.

Hemos pues obtenido , coeficiente de absorción continua del átomo de H neutro en cm² por absorbedor, debido solamente a las transiciones ligado-libre de este elemento. Nuestro propósito, sin embargo, es obtener el coeficiente másico de absorción k_n en cm² por gramo de materia estelar, para lo cual será necesario calcular primero , el coeficiente de absorción continua del H expresado en cm² por átomo de H neutro. En este contexto, átomos de H neutro con diferentes estados de excitación son obsorbedores diferentes. Para obtener el coeficiente debemos sumar sobre n los productos de por la fracción, respecto del total de átomos de H neutro, de absorbedores de cada nivel. Es decir :

, (10.28)

en la cual es el número de absorbedores (átomos de H neutro) en el nivel n por unidad de volumen, N el número total de átomos de H neutro por unidad de volumen y n₀ representa el nivel más bajo a partir del cual comienzan las contribuciones al coeficiente . Para l = 9000 Å, por ejemplo, n₀ = 4 (Figura 10-3), ya que para esa longitud de onda no hay contribución para los tres primeros valores de n.

3000

2000

1000

0

0 2 4 6 8 10 12 14 16 18

Figura 10-3 : Coeficiente de absorción correspondiente a las transiciones ligado-libre del átomo de hidrógeno.

La fracción puede obtenerse de la ley de Boltzmann (4.7) aplicada al átomo de H :

, (10.29)

en la cual g_n es el peso estadístico del nivel n, la función de partición del átomo de H neutro y el potencial de excitación del nivel n. Para el átomo de H es y = 2, en tanto que el potencial de excitación es, por definición, . Dado que y además , resulta :

(10.30)

Luego, de (10.24), (10.28) y (10.29) se obtiene para la expresión :

(10.31)

De la Figura 10-3 se desprende que para una determinada longitud de onda, la principal contribución al coeficiente está dada por los tres primeros términos. Unsöld (1955) introdujo una importante simplificación al demostrar que la pequeña contribución producida por los niveles más elevados puede reemplazarse por la siguiente integral :

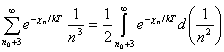, (10.32)

lo que resulta evidente si se tiene en cuenta que . Unsöld supuso además que = 1 para , lo que puede considerarse razonable ya que la integral de Unsöld es despreciable frente a los tres primeros términos no incluidos en dicha integral . A su vez, de (10.30) es :

, (10.33)

y en consecuencia la integral de Unsöld puede escribirse en términos de la variable de la siguiente manera :

, (10.34)

en la cual es el potencial de excitación del nivel dado por :

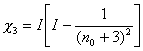(10.35)

Resolviendo la integral de (10.34) se obtiene :

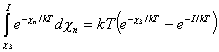(10.36)

De las expresiones (10.31), (10.34) y (10.36), con la suposición de que = 1 para , resulta :

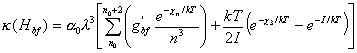(10.37)

La (10.37) muestra la dependencia del coeficiente no sólo con la longitud de onda y el nivel n, sino también con la temperatura T y los potenciales de ionización y excitación del átomo de H. En ocasiones, en lugar de la temperatura suele usarse el parámetro . Si la constante de Boltzmann k se expresa en electrón-volts y la temperatura T en grados Kelvin, el parámetro Q puede escribirse como :

, (10.38)

por lo que es válida la igualdad : (10.39)

La (10.39) da lugar a las siguientes igualdades : y , las cuales permiten expresar finalmente el coeficiente en términos de la variable Q de la siguiente manera :

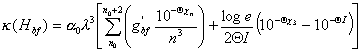, (10.40)

en la cual loge = 0.43429 y a₀ = 1.044x10^-26.

Nótese que el coeficiente graficado en la Figura 10-3 tiene unidades de cm² por absorbedor. Si se quisiera comparar esta figura con las observaciones, el valor de debería multiplicarse primero por el número de absorbedores correspondientes a cada nivel n, sumarse luego estos productos y finalmente invertir el sentido del crecimiento del coeficiente . Es interesante destacar que, como resultado de todo este proceso, la variación del coeficiente con la longitud de onda, reproduce bastante bien la distribución observada usualmente en la región visual e infrarroja cercana del espectro.

10.7.2 Procesos libre-libre

Procederemos ahora a examinar la contribución de los procesos libre-libre del H a la absorción continua. Si bien en la región visible del espectro, la contribución de los procesos libre-libre del H es mucho menor que la correspondiente a los procesos ligado-libre, en el infrarrojo ocurre precisamente lo contrario. Aunque pueden ocurrir interacciones libre-libre entre electrones y electrones, por lo general es más probable la interacción entre electrones y protones. Una transición radiativa libre-libre ocurre cuando un electrón libre moviéndose en el campo de un protón absorbe un fotón y éste desaparece. Como consecuencia de esta interacción, la energía del electrón aumenta en la energía del fotón. La capacidad de absorber del electrón libre depende de su energía total , o bien de su velocidad v. Esto es así por analogía a lo que ocurre en el caso del átomo de H neutro. En efecto, en este último caso y de acuerdo a la expresión (10.24), el coeficiente de absorción a_n en cm² por absorbedor depende del estado de excitación del átomo (n), ya que cuanto mayor es n, menor es la velocidad del electrón en su órbita, pero mayor es la energía total del átomo. Análogamente, cuando mayor es la energía total del electrón libre, menor es su capacidad de absorber. La absorción dependerá entonces de la velocidad del electrón. Haciendo uso de la Física Clásica, Kramers (1923) ha mostrado que la contribución de los procesos libre-libre al coeficiente de absorción continua en cm² por ión (protón) y por electrón libre moviéndose con velocidad entre v y v+dv, está dada por :

(10.41)

Si suponemos que los electrones tienen una distribución Maxwelliana de velocidades, la absorción completa o contribución total se obtendrá multiplicando la contribución por la fracción de electrones expresada en (4.29) e integrando este producto sobre la velocidad. Resulta así :

(10.42)

Para resolver la integral anterior, hacemos la sustitución , de manera que . Con este cambio de variables se obtiene :

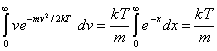, (10.43)

y la (10.42) puede escribirse de la siguiente manera :

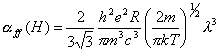(10.44)

La derivación de Gaunt usando la Mecánica Cuántica conduce a la misma expresión, aunque multiplicada por un factor , conocido como factor de Gaunt para las transiciones libre-libre.

Por consideraciones análogas al caso de las transiciones ligado-libre, el coeficiente de absorción expresado en cm² por átomo de H neutro, se obtiene multiplicando por el cociente , en el cual y son los números de iones (protones) y electrones por unidad de volumen, respectivamente, y el número de átomos de H neutro por unidad de volumen. Este cociente puede obtenerse de la fórmula de Saha (4.12) aplicada al H, a saber :

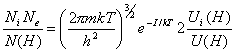, (10.45)

en la cual y son las funciones de partición del átomo de H ionizado y neutro, respectivamente. Dado que el átomo de H ionizado (protón) no posee electrones que puedan estar excitados, sólo puede existir en una única forma. Su peso estadístico para el nivel fundamental es entonces la unidad y la función de partición también, es decir, = 1. Por su parte, el átomo de H neutro en el nivel fundamental puede existir en dos maneras diferentes, con su único electrón con el spin hacia arriba o hacia abajo, de manera que el peso estadístico del nivel fundamental es ahora 2. Las energias de excitación para los restantes niveles (n > 1) son tan elevadas que los números de partículas en estos estados pueden despreciarse en comparación con el número de partículas en el nivel fundamental. Podemos entonces aceptar que = 2. La (10.45) se transforma entonces en :

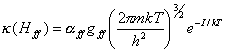(10.46)

Finalmente, teniendo en cuenta (10.38) y (10.39), considerando que es el potencial de ionización del H neutro y que la constante de Rydberg es por, definición, , resulta después de algunos pasos algebraicos :

, (10.47)

en la cual : (10.48)

El factor de Gaunt necesario para calcular de (10.47) ha sido tabulado por Karzas y Latter (1961), Gingerich (1964), y otros autores. Las siguientes expresiones han sido dadas por Menzel y Pekeris (1935) para el factor de Gaunt :

(10.49)

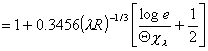, (10.50)

en la cual = 1.2398 x10⁴/l es la energía del fotón cuando l está dada en angstroms.

Hemos obtenido el coeficiente de opacidad continua en cm² por átomo de H neutro, tanto para las transiciones ligado-libre como para las libre-libre del átomo de H. Dado que la distribución espectral de energía en las estrellas de tipos B, A y F muestra una fuerte modulación debida al coeficiente de absorción del H neutro, tenemos prácticamente resuelto el problema del coeficiente de absorción para estas estrellas. En las estrellas más calientes de tipos espectrales O, el hidrógeno neutro deja de ser el absorbedor continuo dominante en virtud de que hay mucho menor cantidad de estos átomos. En este caso, dada la abundancia de electrones libres, comienza a ser importante la dispersión electrónica. Por su parte, en los tipos espectrales G tempranos, como el Sol, veremos en seguida que se dan las condiciones óptimas para la formación de iones negativos del H, por lo que el espectro continuo en la región visible de estas estrellas, estará dominado por la absorción de estos iones. Finalmente, en las estrellas tardias tipo M abundan los compuestos moleculares y, por lo tanto, el proceso físico dominante es ahora la dispersión Rayleigh.

10.8 EL IÓN NEGATIVO DEL HIDRÓGENO

En ciertas condiciones, el átomo de hidrógeno puede capturar un segundo electrón y mantenerlo ligado. Cuando esto ocurre, el átomo de H queda ionizado negativamente, por lo que se denomina ión negativo del hidrógeno y se lo denota con el símbolo . Si bien en la década del 30 cálculo teóricos basados en la Mecánica Cuántica permitieron predecir la existencia de este ión, fue Wildt (1939) quien por vez primera sugirió que los iones negativos del H son los responsables de la mayor parte de la absorción continua observada en el Sol. Cálculos muy precisos han confirmado que para liberar el segundo electrón del se requiere una energía de apenas 0.754 eV. Precisamente, dado que la energía de ligadura del segundo electrón ligado es tan baja, un pequeño cambio en las condiciones del gas es suficiente para que el expulse el segundo electrón y se convierta nuevamente en un átomo de H neutro.

El no se puede excitar y por ende no da lugar a transiciones discretas, esto es, no existen líneas espectrales debidas al . Cualquier fotón con una energía hn mayor que la energía de ligadura del (0.754 eV) puede liberar el segundo electrón ligado al y transformarlo nuevamente en un átomo de H neutro. Un proceso de este tipo corresponde a una transición ligado-libre del . Dado que un fotón con una energía de 0.754 eV tiene una longitud de onda asociada de 16.450 Å, todos los fotones con longitudes de onda asociadas menores que dicha cantidad tendrán suficiente energía como para fotoionizar el y neutralizarlo. Los cuantos de energía hn que pueden ser absorbidos por el son infinitos y varían con continuidad a partir de la energía umbral hn = 0.754 eV, de manera pues que las transiciones radiativas ligado-libre del contribuyen al espectro continuo.

El no sólo puede absorber energía mediante transiciones ligado-libre como las descriptas precedentemente, sino que también pueden ocurrir transiciones libre-libre producidas por este ión. En efecto, puede ocurrir una transición libre-libre como resultado de una interacción entre un átomo de H neutro y un electrón. El conjunto formado por estas dos partículas, aún cuando el electrón no esté ligado al átomo, constituye un sistema tipo , de la misma manera que un protón y un electrón, aún cuando este último no esté ligado al protón, constituye un sistema tipo átomo de H neutro. La única diferencia entre un protón y un electrón libre y el átomo de H neutro radica en el hecho de que el electrón del primer sistema tiene energías positivas y no negativas, como en el átomo de H neutro. Podríamos decir, en este caso, que el electrón se encuentra debilmente ligado al protón. Análogamente, cuando se considera un electrón libre y un átomo de H neutro, puede considerarse que en cierta manera el electrón se encuentra débilmente ligado al átomo de H neutro, constituyendo en conjunto un sistema tipo. El electrón libre, en este último caso, dispone de un conjunto continuo de energías positivas permitidas. Por lo tanto, un electrón desplazándose en una órbita hiperbólica alrededor de un átomo de H neutro, puede absorber un fotón hn y pasar a otra órbita hiperbólica más lejana. En este caso, se dice que hubo una contribución al coeficiente de absorción continua debido a una transición ligado-libre del .

Podríamos preguntarnos qué condiciones físicas y químicas deben existir en una fotosfera para que puedan formarse iones negativos del H ? Esencialmente se requiere una mezcla de átomos de H neutro con átomos de otros elementos químicos cuyos potenciales de ionización sean muy bajos en comparación con el potencial de ionización de H. Esta mezcla debe encontrarse naturalmente a baja temperatura, para permitir que los electrones que han escapado de los átomos de bajo potencial de ionización puedan ligarse fácilmente a los átomos de H neutro y formar iones estables. Si una fotosfera estelar estuviese íntegramente constituida por átomos de H neutro, la baja temperatura requerida para la estabilidad del no permitiría que existieran electrones libres debido a que el potencial de ionización del átomo de H (13.6 eV) es mucho mayor que la energía necesaria para formar el (0.754 eV). En consecuencia, no sería posible encontrar iones en una fotosfera de puro H neutro, aún cuando la misma se encontrara a bajas temperaturas.

¿ En qué tipos espectrales se dan las condiciones para la formación de iones negativos del hidrógeno en cantidades apreciables ? Podemos mostrar que las temperaturas y presiones electrónicas típicas de los tipos espectrales tardíos, próximos al tipo solar, son apropiadas para la formación del . En efecto, si se trata el caso particular de la fotosfera solar y se suponen condiciones de equilibrio termodinámico, la proporción de iones respecto de átomos de H neutro, o viceversa, puede obtenerse a partir de la ley de Saha (4.14) escrita de la siguiente manera :

, (10.51)

en la cual y representan los números de átomos de H neutros y iones por unidad de volumen, respectivamente, es la función de partición del , I el potencial de ionización del , Q = 5040/T y P_e la presión electrónica. Nótese que el ión no tiene estados excitados con energías menores que la energía de ionización, de manera que para calcular la función del partición del sólo tenemos que considerar el peso estadístico del nivel fundamental. Si bien el tiene dos electrones ligados, ambos están en el nivel n = 1. De acuerdo al Pricipio de Pauli, estos dos electrones no pueden tener todos sus números cuánticos iguales, por lo que la única configuración posible para el es que un electrón tenga su spin para arriba y el otro para abajo. Esto significa que el peso estadístico del en el nivel fundamental debe ser la unidad, o sea, = 1.

Para una región típica fotosférica en el Sol T » 6000 K (Q = 0.84) y log P_e (dinas/cm²) = 1.5, de manera que (10.51) implica :

x, (10.52)

lo que equivale a decir que, en las condiciones consideradas y en la unidad de volumen, existen aproximadamente unos 25 millones de átomos de H neutro en la fotosfera solar por cada . Este resultado aparenta contradecir la aseveración original de Wildt (1939), en el sentido de que los iones son los responsables de la mayor parte de la absorción continua observada en el Sol. Veremos, sin embargo, que no existe tal contradicción.

Comparemos la cantidad de iones por unidad de volumen, con el número de átomos de H neutro por unidad de volumen en condiciones de absorber energía en la región visible del espectro. En particular, si llamamos a la densidad de átomos de H neutro en el tercer nivel (n = 3) en condiciones de absorber el continuo de Paschen, la fórmula de Boltzmann (4.9) implica :

, (10.53)

en la cual es el peso estadístico del tercer nivel del H y el correspondiente potencial de excitación. Dado que para el átomo de H es , entonces = 18. Además, puesto que I = 13.6 eV y de (10.30) se obtiene = 12.09, resulta :

x10⁹, (10.54)

De (10.53) y 10.54) resulta :

(10.55)

Existe pues un gran número de iones en comparación con el número de átomos del H neutro en condiciones de absorber el continuo de Paschen. Puede mostrarse que el número de iones es también mayor que el de átomos de H neutro en condiciones de absorber el continuo de Balmer y aún mayor que el de átomos de H neutro en condiciones de absorber las restantes series espectrales del H. En efecto, los cálculos muestran que :

160 , etc

Llegamos entonces a la conclusión de que, en las condiciones consideradas, no obstante ser los iones mucho menos abundantes que los átomos de H neutro, prevalecen numéricamente cuando se los compara con los átomos de H en condiciones de absorber en la región visible e infrarroja del espectro. Ésta es la razón por la cual la contribución del a la opacidad continua en las fotosferas tipo solar, es mucho mayor en la región visible e infrarroja del espectro que la contribución de los átomos de H neutro.

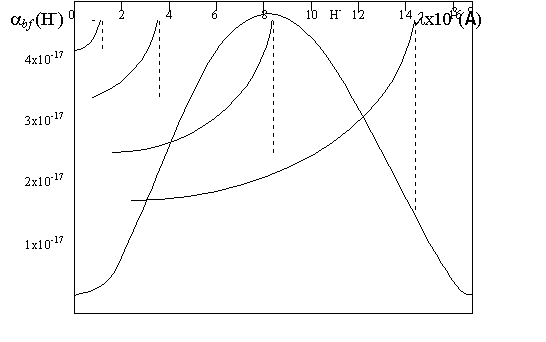
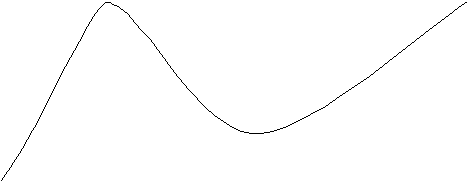
Figura 10-4 : Coeficiente de absorción continua debido a las transiciones ligado-libre del ión negativo del hidrógeno, comparado con el correspondiente al átomo de H neutro en el nivel fundamental y en sus primeros estados excitados.

Dado que el potencial de ionización del es 0.754 eV, la absorción continua debida a la fotodisociación del se extiende desde l = hc/0.754 eV = 16450 Å en el infrarrojo hacia las longitudes de onda más cortas, cubriendo todo el rango espectral visible con un máximo en aproximadamente 8500 Å (Figura 10-4). La importancia astrofísica del radica precisamente en que los cuantos de energía de la región visible e infrarroja del espectro pueden fotodisociar este ión. Nótese de paso que la fotodisociación del equivale a una transición radiativa ligado-libre del ión negativo del hidrógeno.

Varios autores han llevado a cabo complicados cálculos teóricos del coeficiente de absorción continua del debido a las transiciones ligado-libre. Los primeros esfuerzos realizados, entre otros, por Massey y Bates (1940) y Wheeler y Wildt (1942), fueron sólo parcialmente exitosos y muy poco después mejorados por Chandrasekhar y sus colaboradores. Cálculos detallados fueron posteriormente realizados por Ohmura y Ohmura (1960), Geltman (1962), Doughty et al. (1966) y Krogdahl y Miller (1967). Todos estos cáculos demuestran que el coeficiente de absorción debido a las transiciones ligado-libre del no varía con el cubo de la longitud de onda, como acontece con el átomo de H neutro. Por el contrario, es aproximadamente constante en un rango espectral relativamente amplio. De la Figura 10-4 se aprecia que el coeficiente de absorción ligado-libre del tiene un máximo cuyo valor supera en aproximadamente un orden de magnitud al correspondiente coeficiente ligado-libre del átomo de H neutro. Nótese además que el máximo del aporte del ocurre aproximadamente en 8500 Å y, en la región visible entre 4500 Å y 7000 Å, dicho coeficiente varía bastante poco con la longitud de onda. De acuerdo a Geltman (1962), los siguientes polinomios ajustan muy bien el coeficiente :

x

x

x , (10.56)

válido para 1500Å < l < 5250Å y :

x

x

x , (10.57)

válido para 5250Å < l < 11250Å, y :

x

x

x , (10.58)

válido para 11250Å < l < 15000Å.

El coeficiente en los polinomios anteriores está expresado en cm² por ión y por unidad de presión electrónica. Nótese que en ningún caso se ha incluido el factor de emisiones estimuladas.

Para obtener el coeficiente de absorción continua debido a las transiciones ligado-libre del , expresado en cm² por átomo de H neutro, tenemos que multiplicar por la fracción de iones respecto del número de átomos de H neutro. De las expresiones (4.16) y (4.17) se tiene :

x x , (10.59)

en la cual se ha tenido en cuenta que = 1 y = 2. Dado que eV, resulta :

x (10.60)

La componente libre-libre del se hace importante recién en el infrarrojo. Los cálculos teóricos son bastante complejos y han sido realizados, entre otros, por Chandrasekhar y Breen (1946), John (1966), Geltman (1965), Doughty y Fraser (1966) y Stilley y Callaway (1970). En la Figura 10-5 se muestra el comportamiento en función de la longitud de onda del coeficiente expresado en cm² por ión , de acuerdo a los cálculos teóricos de Stilley y Callaway (1970). Este coeficiente se hace claramente importante en el infrarrojo y es mayor cuanto menor es la temperatura. Si bien en las estrellas M deberia ser teóricamente importante, en estas estrellas no hay electrones libres como para formar el .

Figura 10-5 : Comportamiento del coeficiente en cm² por de acuerdo a los cálculos de Stilley y Callaway (1970).

El siguiente polinomio ajusta dentro del 1% los cálculos de Stilley y Callaway (1970) en el rango espectral 3038-91130 Å y para temperaturas entre 2500 ^oK y 10.100 ^oK :

, (10.61)

en el cual es :

,

,

,

y la emisión estimulada ya ha sido tenida en cuenta en (10.61). Si bien el gráfico de la Figura 10-5 vale para una determinada presión electrónica P_e, la tendencia manifiesta en el diagrama es independiente de P_e.

En la Figura 10-6 se ilustra el comportamiento del coeficiente de absorción continua del ión para una temperatura de 6300 ^oK, debido a transiciones ligado-libre y libre-libre. La cantidad graficada es 10²⁶ veces el coeficiente de absorción por átomo de H neutro y por unidad de P_e.

5

4

3

2

1

0

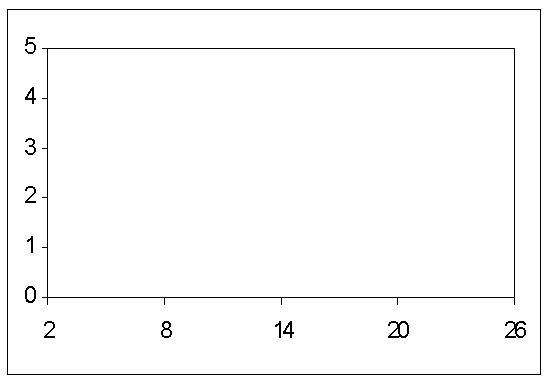
2 8 14 20 26

Figura 10-6 : Coeficiente de absorción continua debido a las transiciones ligado-libre y libre-libre del ión negativo del H, para una temperatura de 6.300 ^oK. La cantidad graficada es 10²⁶ veces el coeficiente de absorción por átomo de H neutro y por unidad de presión electrónica.

10.9 ABSORCIÓN CONTINUA DEBIDA A LA MOLÉCULA DE HIDRÓGENO

Otro absorbedor continuo hidrogenoide es la molécula de hidrógeno H₂, cuya abundancia supera la del hidrógeno atómico en las estrellas tipo M. Si bien esta molécula no absorbe en la región del visible, si lo hacen sus respectivos iones y . El ión positivo consiste de dos protones y un electrón, en tanto que el ión está formado por dos protones y tres electrones. Dado que la densidad de iones es proporcional al producto de la densidad de atomos de H neutro por la densidad de protones, el ión positivo contribuye en forma significativa a la opacidad continua sólo en un rango de temperaturas y presiones dentro del cual existen protones y átomos de H neutro en cantidades apreciables. Este rango ocurre precisamente en las fotosferas de las estrellas de tipo A, en las cuales existen aproximadamente las mismas cantidades de H neutro y ionizado. De allí que aproximadamente el 10% de la opacidad continua en el visible de estas estrellas se debe al aporte del ión . La contribución de este ión a la opacidad continua ha sido estudiada, entre otros, por Bates (1951, 1952), Buckingham et al. (1952), Ledsham y Stewart (1953) y Matsushima (1964). Este último demostró que para estrellas frias, la contribución del ión es menor que el 10% de la del para l > 4000 Å. Doyle (1968) estudió la absorción producida por la llamada molécula cuasi-H₂ y encontró que su contribución es significativa en la región del ultravioleta (l < 2500 Å) y en estrellas tipo solar.

Por su parte, el ión existe sólo a temperaturas comparativamente bajas propias de las estrellas M. Si bien los procesos ligado-libre de este absorbedor son prácticamente despreciables, no lo son los procesos libre-libre, los cuales aportan en forma significativa en el infrarrojo lejano. Los coeficientes de absorción debidos a transiciones libre-libre del ión han sido calculados, entre otros, por Somerville (1964) y Dalgarno y Lane (1966). El coeficiente de absorción de acuerdo a estos últimos autores es :

x

cm⁴ dinas^-1 , (10.62)

en la cual a = (1.439 x 10⁸)/kT, con l medida en anstroms.

10.10 OPACIDAD CONTINUA DEBIDA AL HELIO

10.10.1 Contribución del HeI y HeII

Puesto que el He es el elemento más abundante después del hidrógeno en la gran mayoría de las estrellas, podría pensarse que su contribución al coeficiente de absorción continua debe ser también apreciable. Ciertamente, en algunas estrellas con abundancias anormalmente grandes de He, la opacidad continua puede estar dominada por este elemento químico. Recordemos que el He se observa en los espectros estelares, tanto en estado neutro como en estado una vez ionizado. Sin embargo, dado que el potencial de ionización del HeI es bastante elevado (24.58 eV), su contribución se aprecia sólo en estrellas O y B a elevadas temperaturas, en las cuales el H está fuertemente ionizado. Los primeros niveles del HeI tienen energías de excitación de alrededor de 20 eV y el borde de absorción a partir del nivel fundamental yace en 504 Å, de manera que la contribución de este elemento será importante sólo en el ultravioleta lejano de estrellas tempranas. Como en el caso del H, el coeficiente de absorción del HeI en una determinada longitud de onda, se obtiene sumando las contribuciones de cada uno de los continuos que se extienden más allá de las diferentes series espectrales de este elemento. Para una temperatura típicamente solar (6000 ^oK), la fórmula de Boltzmann (4.3) implica:

, (10.63)

en la cual el cociente indica la fracción de átomos de He en el primer nivel excitado (n = 2) respecto de átomos de He en el nivel fundamental (n = 1). A estas temperaturas prácticamente todos los átomos de He se encuentran en el nivel fundamental. Si bien pueden ocurrir transiciones ligado-libre desde el nivel fundamental en longitudes de onda más cortas que l = 504 Å, es muy pequeña la radiación que emite el Sol en esta región del espectro.

A muy elevadas temperaturas, características de las estrellas O, tanto el H como el He se encuentran altamente ionizados. En estas condiciones, la contribución del HeII como fuente de opacidad continua puede comenzar a ser importante. Este ión consiste en un electrón y un núcleo con carga Z = 2, siendo su energía de ionización de 54.4 eV. Debido a que la opacidad del HeII depende fuertemente de la temperatura, normalmente puede despreciarse su contribución, excepto para las estrellas B0 o más tempranas. El HeII puede contribuir también en las capas más profundas de estrellas algo más frías que las mencionadas. Ueno et al. (1954) han publicado tablas con valores del coeficiente de absorción del HeI para temperaturas entre 10.080 ^oK y 50.400 ^oK y del coeficiente de absorción del HeII, para temperaturas entre 25.200 ^oK y 50.400 ^oK en ambos casos en la región del ultravioleta entre 228 Å y 2279 Å.

10.10.2 El ión negativo del helio

El ión negativo del helio, denotado , se forma cuando un átomo de He con dos electrones y dos protones, captura un tercer electrón y lo mantiene ligado al átomo. La energía de ligadura del tercer electrón ligado es de 19 eV, es decir, se trata de una energía bastante apreciable. Al igual que el ión , el ión no se puede excitar, esto es, no existen posibles transiciones ligado-ligado del . Cualquier fotón con una energía hn mayor que 19 eV podrá ionizar el ión y transformarlo nuevamente en un átomo de He neutro. Dado que la longitud de onda asociada a este fotón es 652 Å, todos los fotones con l £ 652 Å están en condiciones de producir transiciones ligado-libre del . Estas transiciones, sin embargo, son despreciables para casi todas las estrellas, excepto quizás para las estrellas O muy calientes. Esto se debe a que la gran mayoría de las estrellas no irradian energías suficientemente grandes como para arrancar el tercer electrón ligado al ión .

Un proceso libre-libre del ión ocurre por interacción de un átomo de He neutro con un electrón con energía positiva. Si el electrón libre moviéndose en el campo del átomo de He neutro absorbe un fotón, cambiará su órbita hiperbólica, alejándose del átomo. Dado que las energías que pueden ser absorbidas por este proceso son infinitas y varían con continuidad, los procesos libre-libre del contribuyen a la opacidad continua. Estos procesos pueden ser importantes en particular para longitudes de onda grandes y en estrellas frías. McDowell et al. (1966) y John (1968) han calculado teóricamente el coeficiente de absorción continua para las transiciones libre-libre del , y han incluído en sus cálculos las emisiones estimuladas. El siguiente polinomio ajusta muy bien los resultados de McDowell et al. (1966) :

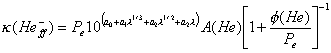, (10.64)

en el cual el término exponencial está expresado en cm² por átomo de HeI y es la abundancia relativa (por número de átomos) del He respecto del H; es decir, = (HeI+HeII)/N_H representa el cociente entre el número de partículas de helio (HeI + HeII), por unidad de volumen, sobre el número de partículas de hidrógeno (HI + protones), por unidad de volumen. Nótese que el factor entre corchetes en (10.64) tiene en cuenta la ionización del He a elevadas temperaturas. En efecto, si se aplica la fórmula de Saha (4.16) al átomo de He, se tiene :

, (10.65)

en la cual el primer miembro representa el cociente entre el número de átomos de He ionizados, por unidad de volumen, respecto del número de átomos de He neutro, por unidad de volumen, y es la función de partición correspondiente al He neutro. La (10.65) puede escribirse como :

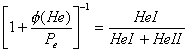, (10.65)

de manera que el coeficiente en (10.64) resulta expresado en cm² por partícula de H y por unidad de presión electrónica. Los coeficientes en (10.64) son :

Además de los iones negativos y , existen también iones negativos correspondientes a otros elementos químicos o a compuestos moleculares que aportan a la opacidad continua. Brascomb y Pagel (1967), por ejemplo, analizaron la posible importancia astrofísica de la absorción producida por iones negativos tales como , , , y . Estos autores llegaron a la conclusión de que los iones negativos y son los más importantes. Por su parte, Vardya (1967) ha mostrado que otros iones negativos tales como , y , se presentan con cierta abundancia en estrellas tardías y es posible que en ellas estos iones contribuyan levemente.

10.11 OPACIDAD CONTINUA DEBIDA A LOS METALES

Además del H y del He contribuyen a la opacidad continua los metales en general, cuyas absorciones ligado-libre pueden ser importantes en la región del ultravioleta. Esfuerzos pioneros en el cálculo de coeficientes de absorción de algunos metales han sido realizados, entre otros, por Vitense (1951) y Seaton (1958). Una manera de determinar el coeficiente de absorción de los metales es tomar las secciones transversales calculadas teóricamente (cuando existen) y multiplicarlas por el respectivo número de absorbedores. De esta manera Rich (1967), por ejemplo, obtuvo para el silicio el valor 37x10^-18 cm² por absorbedor para el estado fundamental, con lo que fue posible demostrar que para T = 5600 K y P_e = 10 dinas/cm², el silicio domina la opacidad metálica en el ultravioleta entre aproximadamente 1300 Å y 2000 Å. En muchos casos, sin embargo, las secciones transversales no se conocen con precisión. Peach (1967) y Travis y Matsushima (1968) utilizaron el método conocido como del defecto cuántico (Burgess y Seaton 1960) y produjeron extensas tablas con coeficientes de absorción. Sobre la base de cálculos simples, Böhm-Vitense (1989) ha mostrado que en una fotosfera tipo solar y en el ultravioleta (l = 2000 Å), las absorciones metálicas - particularmente del Fe - son mucho más importantes que las producidas por el ión o el átomo de H neutro.

10.12 DISPERSIÓN POR ELECTRONES

Como se mencionara en las Secciones 6.8 y 10.2, la radiación continua puede ser no sólo absorbida realmente, sino también dispersada dando lugar a una absorción aparente. En el primer caso el fotón desaparece y su energía contribuye a incrementar al menos parcialmente la energía térmica del gas, en tanto que en el proceso de dispersión o scattering el fotón no desaparece, sino que es desviado respecto de su dirección original, pudiendo incluso modificarse ligeramente su frecuencia (dispersión no coherente).

La dispersión de la radiación producida por electrones libres se conoce como dispersión electrónica o scattering Thompson. La fórmula clásica de Thompson, cuya deducción puede verse en Mihalas (1970), indica que el coeficiente de scattering (sección transversal) del electrón está dado por :

, (10.66)

en la cual e y m representan la carga y la masa del electrón, respectivamente, y está expresado en cm² por electrón. Es decir, este coeficiente equivale a 8/3 de la sección eficaz del electrón calculada a partir del radio clásico del mismo, . Es importante notar que el coeficiente es independiente de la frecuencia de la radiación incidente. De medidas cuidadosas realizadas en el laboratorio se obtiene para este coeficiente el siguiente valor :

, (10.67)

el cual ha sido verificado por cálculos realizados con ayuda de la Mecánica Cuántica en el límite correspondiente a fotones de baja energía, esto es, . Cuando se consideran fotones de muy alta energía, con longitudes de onda asociadas l < 1 Å (radiación X), puede emplearse para el cálculo la fórmula de Klein-Nishina (Heitler 1954), la cual predice un coeficiente algo menor que el indicado en (10.67). En la práctica, puede sin embargo ignorarse esta diferencia en las fotosferas estelares.

Si bien, en principio, puede ocurrir scattering por núcleos atómicos, este proceso resulta despreciable en virtud de que el cociente 1/m² en (10.66) es demasiado pequeño. En el caso más general el scattering por electrones no es isotrópico, sino que existen direcciones preferenciales para la dispersión (anisotropía intrínseca del proceso). Sin embargo, en una fotosfera estelar, en promedio, la dispersión por electrones es o se considera isotrópica.

Dado que este mecanismo de absorción aparente resulta importante en atmósferas a elevadas temperaturas donde abundan los electrones libres, suele expresarse este coeficiente de absorción en cm² por partícula de H - en lugar de cm² por átomo de H neutro - de la siguiente manera :

, (10.68)

en la cual representa el cociente entre la densidad electrónica y la densidad de partículas de H (átomos de HI + protones), P_e es la presión electrónica y P_H la presión parcial debida al H.

¿ Qué relación existe entre la presión y la presión del gas ? Nótese que la fotosfera de una estrella contiene otros elementos químicos además del H. Si N representa la densidad total de partículas, entonces :

, (10.69)

en la cual es la densidad de partículas del tipo i y la densidad electrónica. De acuerdo a (10.1), definimos la abundancia relativa al hidrógeno (por número de partículas) como :

(10.70)

De (10.69) y (10.70) resulta:

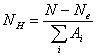(10.71)

Multiplicando ambos miembros por se obtiene la relación buscada :

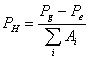, (10.72)

en la cual es la presión del gas. Reemplazando (10.72) en (10.68) resulta :

, (10.73)

en la cual como hemos visto está expresado en cm² por partícula de H.

Resulta evidente que la emisión estimulada no debe ser incluída en este caso, ya que estamos considerando un proceso de absorción aparente, no real. Nótese además que el scattering Thompson es un caso particular del efecto Compton, ya que si se consideran fotones con bajas energías en relación a la energía en reposo de los electrones, no ocurre prácticamente cambio alguno en la frecuencia del fotón dispersado. A medida que aumenta la energía del fotón, aumenta el enrojecimiento del mismo por efecto Compton.

Para tener una idea de la cantidad en la que puede contribuir la dispersión electrónica a la opacidad continua, debe tenerse presente que en las estrellas de la secuencia principal (clase de luminosidad V), la presión del gas es aproximadamente del mismo orden que la presión del H y ambas tienen valores entre 10³ y 10⁵ dinas/cm². Si se tiene en cuenta (10.68), estos valores implican por partícula de H, cantidad ésta muy pequeña comparada con los otros procesos de absorción. Por el contrario, en las estrellas supergigantes (clase de luminosidad I), la presión del gas oscila entre 10 y 100 dinas/cm², de manera que el coeficiente por unidad de presión electrónica resulta entre dos y tres órdenes de magnitud mayor.

Si se desea obtener el coeficiente de absorción por dispersión electrónica expresado en cm² por gramo de materia estelar, basta multiplicar el coeficiente (expresado en cm² por electrón) por el cociente , estando la densidad r expresada en gr/cm³. Es decir, de acuerdo a la notación adoptada en la Sección 10.3, se tendrá :

, (10.74)

en donde ahora está expresado en cm² por gramo de materia estelar.

En la fotosfera solar (T » 6000 ^oK, Q = 0.84), el cociente entre la densidad electrónica y la densidad de átomos de H neutro es aproximadamente similar al cociente entre entre la presión electrónica y la presión del gas. El valor de este cociente es del orden de 3x10^-3. Si se compara este valor con el obtenido antes en (10.52), se advierte que en la fotosfera solar son mucho más abundantes los electrones libres que los iones . Sin embargo, dado que el coeficiente por dispersión electrónica es tan bajo comparado con los correspondientes coeficientes de absorción por átomo de H neutro o por ión , la contribución de la dispersión electrónica a la opacidad continua en el Sol es absolutamente despreciable.

10.13 DISPERSIÓN RAYLEIGH

El término dispersión o scattering Rayleigh se refiere a la dispersión de la radiación producida por sistemas ligados, tales como átomos o moléculas. Este caso es esencialmente idéntico a la dispersión electrónica, sólo que la dispersión Rayleigh es producida por partículas de tamaños mucho mayores que los electrones. De allí que este tipo de scattering sea importante en las atmósferas de estrellas de temperaturas moderadamente bajas (tipos G, K y M) donde abundan átomos neutros e incluso compuestos moleculares.

La expresión del coeficiente de absorción debido a dispersión Rayleigh, expresado en cm² por gramo de materia estelar y para un átomo de H es :

, (10.75)

en la cual es el coeficiente de absorción por dispersión electrónica expresado en cm² por gramo de materia estelar y donde l_L = 1026 Å es un promedio pesado de las longitudes de onda de las líneas de la serie de Lyman. La comparación de la longitud de onda incidente l con l_L se debe a que a bajas temperaturas prácticamente todos los átomos de H están en el nivel fundamental y, por lo tanto, se encuentran en condiciones de absorber las líneas de la serie de Balmer. Una deducción simplificada de (10.75) puede verse en Böhm-Vitense (1997).

Es importante notar que la dispersión Rayleigh aumenta con , de manera que los fotones ultravioletas resultan más dispersados que los fotones de la región visible. El color azul del firmamento es esencialmente debido a que la radiación solar sufre dispersión Rayleigh producida por las moléculas de la atmósfera terrestre. La dispersión Rayleigh debida a átomos de H neutro, contribuye a la absorción continua a temperaturas comparativamente bajas y en la región del ultravioleta. A temperaturas aún más bajas (estrellas M) el scattering Rayleigh molecular, particularmente debido a moléculas H₂, prevalece sobre el scattering Rayleigh atómico. Al igual que el scattering electrónico, la dispersión Rayleigh constituye un fenómeno de absorción aparente, motivo por el cual tampoco habrá que corregir por el factor de emisiones estimuladas.

Conforme a lo expresado en la sección anterior, en la fotosfera solar hay aproximadamente 3x10³ veces más átomos de H neutros que electrones libres. En consecuencia, la dispersión Rayleigh debida a esta clase de átomos solamente deja de ser despreciable. Para l << 3000 Å, sin embargo, los coeficientes de absorción de los metales son por lo general mayores que el correspondiente al scattering Rayleigh.

10.14 EL COEFICIENTE DE ABSORCIÓN CONTINUA TOTAL

En la Sección 10.2 hicimos referencia a que la absorción continua observada en una determinada frecuencia en un espectro estelar, resulta de sumar las absorciones (verdaderas y aparentes) producidas en esa frecuencia por determinados procesos físicos (transiciones ligado-libre, libre-libre, dispersión de la radiación, etc), los cuales involucran diferentes elementos químicos en sus respectivos estados de excitación y/o ionización. Vimos además en la Sección 10.5 que las absorciones verdaderas deben ser corregidas por el factor de emisiones estimuladas . Por lo tanto, el coeficiente de absorción continua total debe obtenerse sumando todos los coeficientes de absorción mencionados en este capítulo, corrigiendo por emisión estimulada en los casos que corresponda.

Cuando se consideren los absorbedores continuos hidrogenoides (H, ión , H₂, etc), hay que tener en cuenta que el coeficiente dado en (10.61) ya ha sido corregido por emisiones estimuladas. Luego, el coeficiente k(H) total correspondiente a los absorbedores continuos hidrogenoides, expresado en cm² por átomo de H neutro, será :

, (10.76)

en la cual es el factor de emisiones estimuladas.

Si a elevadas temperaturas se desea tener en cuenta la ionización del H, es conveniente expresar k(H) en cm² por partícula de H y no por átomo de H neutro. Una partícula de hidrógeno es o bien un átomo de H neutro o bien un átomo de H ionizado (protón). Si se multiplica (10.76) por el cociente entre el número de átomos de H neutro (HI) respecto del número de partículas de hidrógeno (HI + HII), el coeficiente k(H) resultará expresado en cm² por partícula de H. La expresión (4.16) aplicada al H es :

, (10.77)

en la cual HII y HI representan las densidades de átomos de H ionizados (protones) y átomos de H neutros, respectivamente. A su vez, (10.77) equivale a :

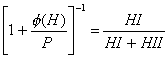(10.78)

Luego, el coeficiente de absorción continua k(H) total, expresado en cm² por partícula de H, es :

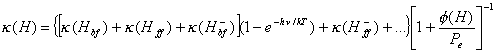(10.79)

Finalmente, el coeficiente k de absorción continua total, expresado en cm² por partícula de H, será :

, (10.80)

en la cual cada uno de los términos que se han agregado en esta expresión deben expresarse en cm² por partícula de H.

La transformación del coeficiente k total, expresado en cm² por partícula de H, al coeficiente k_n total, expresado en cm² por gramo de materia estelar, se logra dividiendo k por la cantidad de de gramos por partícula de H existente en la fotosfera. En efecto, en este caso se tiene :

(10.81)

¿ Cómo puede expresarse la cantidad de gramos (masa) por partícula de H en la fotosfera de una estrella ? Conforme a lo expresado en la Sección 1.1, la masa (en gramos) de un átomo correspondiente al elemento i en la fotosfera, es el cociente entre el peso atómico (expresado en gramos) del elemento i y el número de Avogradro N₀ = 6.0225x10²³. :

(10.82)

Si la abundancia del elemento i, respecto del hidrógeno, es y está dada por (10.70), entonces la cantidad de gramos por partícula de H será simplemente : .

Para expresar el coeficiente de absorción continua total en cm² por gramo de materia estelar debemos pues conocer las abundancias relativas de los diversos elementos químicos que componen la fotosfera. Un valor típico para una atmósfera normal es : = 2x10^-24 gramos por partícula de H.