12 DISPERSIÓN POR ELECTRONES

Como se mencionara en las Secciones 6.8 y 10.2, la radiación continua puede ser no sólo absorbida realmente, sino también dispersada dando lugar a una absorción aparente. En el primer caso el fotón desaparece y su energía contribuye a incrementar al menos parcialmente la energía térmica del gas, en tanto que en el proceso de dispersión o scattering el fotón no desaparece, sino que es desviado respecto de su dirección original, pudiendo incluso modificarse ligeramente su frecuencia (dispersión no coherente).

La dispersión de la radiación producida por electrones libres se conoce como dispersión electrónica o scattering Thompson. La fórmula clásica de Thompson, cuya deducción puede verse en Mihalas (1970), indica que el coeficiente de scattering (sección transversal) del electrón está dado por :

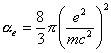, (10.66)

en la cual e y m representan la carga y la masa del electrón, respectivamente, y está expresado en cm² por electrón. Es decir, este coeficiente equivale a 8/3 de la sección eficaz del electrón calculada a partir del radio clásico del mismo, . Es importante notar que el coeficiente es independiente de la frecuencia de la radiación incidente. De medidas cuidadosas realizadas en el laboratorio se obtiene para este coeficiente el siguiente valor :

, (10.67)

el cual ha sido verificado por cálculos realizados con ayuda de la Mecánica Cuántica en el límite correspondiente a fotones de baja energía, esto es, . Cuando se consideran fotones de muy alta energía, con longitudes de onda asociadas l < 1 Å (radiación X), puede emplearse para el cálculo la fórmula de Klein-Nishina (Heitler 1954), la cual predice un coeficiente algo menor que el indicado en (10.67). En la práctica, puede sin embargo ignorarse esta diferencia en las fotosferas estelares.

Si bien, en principio, puede ocurrir scattering por núcleos atómicos, este proceso resulta despreciable en virtud de que el cociente 1/m² en (10.66) es demasiado pequeño. En el caso más general el scattering por electrones no es isotrópico, sino que existen direcciones preferenciales para la dispersión (anisotropía intrínseca del proceso). Sin embargo, en una fotosfera estelar, en promedio, la dispersión por electrones es o se considera isotrópica.

Dado que este mecanismo de absorción aparente resulta importante en atmósferas a elevadas temperaturas donde abundan los electrones libres, suele expresarse este coeficiente de absorción en cm² por partícula de H - en lugar de cm² por átomo de H neutro - de la siguiente manera :

, (10.68)

en la cual representa el cociente entre la densidad electrónica y la densidad de partículas de H (átomos de HI + protones), P_e es la presión electrónica y P_H la presión parcial debida al H.

¿ Qué relación existe entre la presión y la presión del gas ? Nótese que la fotosfera de una estrella contiene otros elementos químicos además del H. Si N representa la densidad total de partículas, entonces :

, (10.69)

en la cual es la densidad de partículas del tipo i y la densidad electrónica. De acuerdo a (10.1), definimos la abundancia relativa al hidrógeno (por número de partículas) como :

(10.70)

De (10.69) y (10.70) resulta:

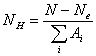(10.71)

Multiplicando ambos miembros por se obtiene la relación buscada :

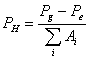, (10.72)

en la cual es la presión del gas. Reemplazando (10.72) en (10.68) resulta :

, (10.73)

en la cual como hemos visto está expresado en cm² por partícula de H.

Resulta evidente que la emisión estimulada no debe ser incluída en este caso, ya que estamos considerando un proceso de absorción aparente, no real. Nótese además que el scattering Thompson es un caso particular del efecto Compton, ya que si se consideran fotones con bajas energías en relación a la energía en reposo de los electrones, no ocurre prácticamente cambio alguno en la frecuencia del fotón dispersado. A medida que aumenta la energía del fotón, aumenta el enrojecimiento del mismo por efecto Compton.

Para tener una idea de la cantidad en la que puede contribuir la dispersión electrónica a la opacidad continua, debe tenerse presente que en las estrellas de la secuencia principal (clase de luminosidad V), la presión del gas es aproximadamente del mismo orden que la presión del H y ambas tienen valores entre 10³ y 10⁵ dinas/cm². Si se tiene en cuenta (10.68), estos valores implican

por partícula de H,

cantidad ésta muy pequeña comparada con los otros procesos de absorción. Por el contrario, en las estrellas supergigantes (clase de luminosidad I), la presión del gas oscila entre 10 y 100 dinas/cm², de manera que el coeficiente por unidad de presión electrónica resulta entre dos y tres órdenes de magnitud mayor.

Si se desea obtener el coeficiente de absorción por dispersión electrónica expresado en cm² por gramo de materia estelar, basta multiplicar el coeficiente (expresado en cm² por electrón) por el cociente , estando la densidad r expresada en gr/cm³. Es decir, de acuerdo a la notación adoptada en la Sección 10.3, se tendrá :

, (10.74)

en donde ahora está expresado en cm² por gramo de materia estelar.

En la fotosfera solar (T » 6000 ^oK, Q = 0.84), el cociente entre la densidad electrónica y la densidad de átomos de H neutro es aproximadamente similar al cociente entre entre la presión electrónica y la presión del gas. El valor de este cociente es del orden de 3x10^-3. Si se compara este valor con el obtenido antes en (10.52), se advierte que en la fotosfera solar son mucho más abundantes los electrones libres que los iones . Sin embargo, dado que el coeficiente por dispersión electrónica es tan bajo comparado con los correspondientes coeficientes de absorción por átomo de H neutro o por ión , la contribución de la dispersión electrónica a la opacidad continua en el Sol es absolutamente despreciable.