3  CONDICIONES DE CONTORNO

 

Hemos ya planteado la ecuación general del transporte radiativo. Nuestro problema inmediato será resolver esta ecuación. Puesto que se trata de una ecuación diferencial, tendremos que fijar algunas condiciones de contorno acordes con la geometría del problema. Consideraremos a continuación dos casos de interés astrofísico, a saber : una capa de espesor finito y una atmósfera semi-infinita.

 

 

3.1 Capa de espesor finito

 

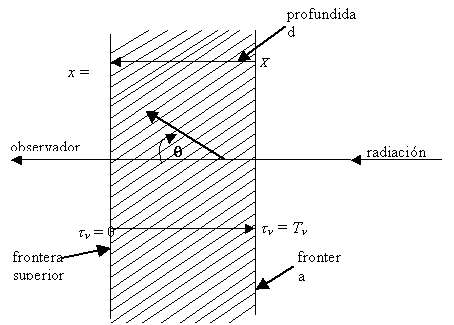
Sea una capa tal como la esquematizada en la Figura 7-6. Dicha capa puede incluir cualquier tipo de material y supondremos que fuera de ella sólo existe el vacío. En la figura hemos indicado la dirección hacia el observador y hemos denominado frontera inferior y superior a las superficies que limitan la capa. Por convención, supondremos que la frontera superior se enfrenta con un hipotético observador. Denotaremos X  a la profundidad geométrica total de la capa y T_n  a la correspondiente profundidad óptica total. Dichas profundidades crecen en sentido contrario y supondremos x = 0  y t_n = 0 en la frontera superior. Mediremos el ángulo q  en el sentido indicado en la figura, de manera que m = cos q  tendrá valores negativos para los rayos que inciden sobre la frontera superior y valores positivos para aquéllos que inciden sobre la frontera inferior.

 

En general, denotaremos con I_n (t_n,m) a la intensidad específica monocromática de un rayo en un punto a profundidad óptica t_n  que forme un ángulo q  (m = cos q) con la dirección hacia el observador. Imponer condiciones de contorno en este caso particular significa especificar los valores de la función I_n en las dos fronteras. Es decir, debemos indicar el valor de la función I_n(0,m) = f_n(m) para –1 £ m < 0 (frontera superior) y de la función I_n(T_n,m) = g_n (m) para 0 < m £ 1 (frontera inferior).

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

	Figura 7-6: Capa de espesor finito.

 

 

 

                                     

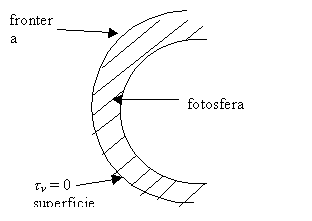
3.2 Atmósfera semi-infinita

 

Este caso, esquematizado en la Figura 7-7, constituye la aproximación que usualmente se hace de una atmósfera estelar. Establecer condiciones de contorno en esta geometría significa especificar la radiación incidente en la frontera superior o superficie de la fotosfera. Usualmente se acepta que no incide radiación sobre la superficie estelar y, en consecuencia, I_n(0,m) = f_n(m) = 0 para –1 £ m < 0. En la frontera inferior la condición de contorno se expresa de la siguiente manera :

 

 

                                            ,                                          (7.14)

 

 

para todos los rayos con 0 < m  £ 1.

 

 

 

En este caso no existe frontera inferior porque admitimos que la fotosfera es semi-infinita. La condición de contorno (7.14) significa simplemente que la radiación proveniente de capas muy profundas no llega a la superficie.

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

	Figura 7-7: Atmósfera semi-infinita, aproximación que usualmente se hace de una atmósfera estelar