6 INTEGRALES EXPONENCIALES
Introduciremos ahora el concepto matemático de integral exponencial, el cual resultará de suma utilidad no sólo
para simplificar los cálculos, sino también para clarificar la interpretación de
ciertas expresiones que deduciremos en la siguiente sección.
Se define la integral exponencial de orden n como una integral impropia de la siguiente manera :
![]() , (7.28)
, (7.28)
en la cual n debe ser un número entero mayor o
igual que la unidad. Una vez fijado el parámetro n, la integral En(x) resulta una función estrictamente
decreciente de la variable x. De la
definición resulta en forma inmediata el valor de la integral exponencial de
orden n en el origen (x = 0) :
![]() (7.29)
(7.29)
Luego: E1(0) = ¥, E2(0) = 1,
E3(0) = 1/2, E4(0) = 1/3, etc. Además, de (7.28) se desprende que para valores
suficientemente grandes de la variable x,
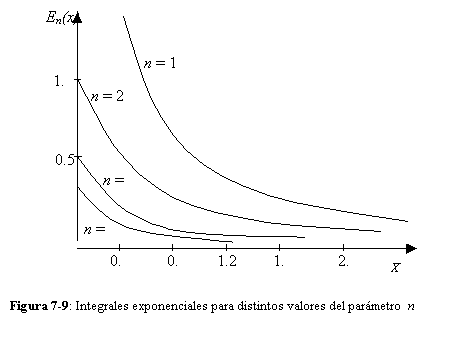
las integrales exponenciales tienden a anularse, cualquiera sea el orden de n. La forma de las integrales
exponenciales se ilustra en la Figura
(7-9).
Existen fórmulas de recurrencia que permiten hallar las integrales
exponenciales En(x) conociendo las integrales
exponenciales En+1(x), o viceversa. En particular, resulta
sencillo demostrar la siguiente relación de recurrencia :
n En+(x) = e-x – x En(x)
(7.30)
Además, si se deriva la expresión (7.28) con respecto a x, se obtiene la siguiente relación
simple entre En(x) y En-1(x) :
![]() (7.31)
(7.31)
Abramowitz y Stegun (1964) encontraron muy buenas aproximaciones para el cálculo de la integral exponencial de primer orden. Dichas expresiones son las siguientes :
E1(x) = - ln x – 0.57721566 +
0.99999193 x – 0.24991055 x2 + 0.05519968 x3 –
-0.00976004 x4 + 0.0010785 x5,
válida para x £ 1.
![]() ,
,
válida para x > 1, donde :
a1 = 8.5733287401 b1 = 9.5733223454
a2 = 18.0590169730 b2 = 25.6329561486
a3 = 8.6347608925 b3 = 21.0996530827
a4 = 0.2677737343
b4 = 3.9584969228
Las expresiones polinómicas obtenidas por los mencionados autores
permiten calcular la integral exponencial E1(x) con un error menor que 2x10-7.