1
CONDICIÓN DE EQUILIBRIO RADIATIVO
El estado físico de cualquier elemento de materia en la fotosfera estelar está determinado por la interacción del mismo con el medio circundante. Consideremos un elemento de volumen DV en la fotosfera estelar y llamemos Eab y Eem a las cantidades totales de energía absorbida y emitida, respectivamente, por ese volumen elemental en la unidad de tiempo. La temperatura dentro del volumen elemental considerado dependerá de la relación que exista entre estas dos cantidades. Si, por ejemplo, Eab es mayor que Eem, la energía interna de DV crecerá continuamente y en consecuencia la temperatura se incrementará. Por el contrario, la inversa será válida si Eab es menor que Eem. Dado que nuestro propósito es estudiar estrellas con atmósferas estacionarias, la temperatura de cualquier elemento de volumen dV de la fotosfera debe permanecer constante en el tiempo. Para que esto ocurra, debe verificarse la siguiente igualdad :
Eab = Eem , (8.1)
conocida como condición de
equilibrio radiativo propiamente dicha.
1.1 Constancia del flujo total
A continuación expresaremos matemáticamente las cantidades de energía involucradas en (8.1) y aplicaremos la condición de equilibrio radiativo propiamente dicha. De la expresión (7.3), la cantidad de energía emitida por un elemento de masa dm contenido en un elemento de volumen dV, dentro de un ángulo sólido dw, en el rango de frecuencias (n,n + dn) y en el tiempo dt, es :
DE(v)em = jv dm dw dn dt
Luego, la cantidad total de energía emitida a todo el espacio por el elemento de volumen considerado es :
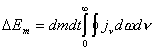(8.2)
Por otra parte, de (7.4)
la cantidad de energía absorbida por el mismo elemento de volumen dV, considerando sólo el ángulo sólido dw, en el rango (n,n + dn) y en el tiempo dt es :
DE (n)ab
= - kn In dm dw dn dt
El valor absoluto de la cantidad total
de energía absorbida desde todas las direcciones por el elemento de volumen
considerado será :
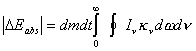(8.3)
Imponer la condición (8-1) implica ahora :
(8.4)
Por otra parte, si integramos la (7.12) sobre todas las frecuencias y 4p estereorradianes resulta :
Suponiendo que la intensidad específica monocromática Iv(q) no
depende del ángulo acimutal f, la igualdad anterior se transforma en :
(8.5)
En virtud de la definición de flujo, el corchete del primer miembro
en la expresión anterior es simplemente el flujo
total F(x) correspondiente a una
cierta profundidad geométrica x.
Además, de (8.4) se desprende que el segundo miembro de (8.5) es nulo. Luego :
(8.6)
Equilibrio radiativo significa conservación de la energía total. Es decir que en una atmósfera en condiciones de equilibrio radiativo, no existen productores ni consumidores de energía. Matemáticamente, esto se expresa mediante la fórmula (8.6) o bien por la relación :
div F(x)
= 0, (8.7)
en la cual F(x) representa el flujo total a la profundidad geométrica x. La condición (8.7) tiene
validez en cualquier lugar de la fotosfera estelar y suele denominarse primera condición de equilibrio radiativo. Esta ecuación puede también escribirse de la siguiente manera :
F(x) = F0 = cte,
(8.8)
en la cual F(x)
representa la cantidad total de energía que atraviesa la unidad de área,
ubicada a la distancia x, en la
unidad de tiempo, en el caso en que toda la energía se transporta por radiación (flujo radiativo); F0 es el flujo total en la superficie.
La constancia del flujo total puede expresarse también en términos
de la temperatura efectiva Te
de la atmósfera.. En efecto, si se tiene en cuenta la expresión (6.5) podemos escribir :
,
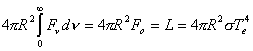en la cual L es la luminosidad y R el radio de la estrella. La constancia
del flujo total se expresa con frecuencia de la siguiente manera :
(8.9)
Cuando se construye un modelo teórico de atmósfera estelar en el que se exige la constancia del flujo total (equilibrio radiativo) como una condición del modelo, resulta evidente de (8.9) que la temperatura efectiva pasa a ser uno de los parámetros fundamentales del problema.
Es importante destacar que la primera condición de equilibrio radiativo es válida sólo en atmósferas planas. En el caso de atmósferas extendidas en las cuales no es posible hacer la suposición de capas planas y paralelas, debe utilizarse la ecuación general del transporte radiativo expresada en (7.9). Si se integra dicha expresión sobre todas las frecuencias y sobre 4p estereorradianes, se obtiene :
(8.10)
Además, si en la atmósfera extendida no existen fuentes ni sumideros de energía de manera que pueda considerarse válida la condición de equilibrio radiativo propiamente dicha, la expresión anterior se reduce a la siguiente :
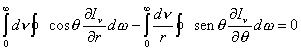(8.11)
Teniendo en cuenta la (6.10), la igualdad anterior puede escribirse de la siguiente manera :
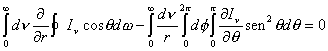
Nótese que una vez fijada la dirección, Fv depende solamente de la coordenada radial, de manera
que es posible escribir :
En consecuencia, se tiene :
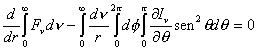(8.12)
Integraremos por partes la última integral del primer miembro de
(8.12). Para ello, haremos el siguiente cambio de variables: m = sen2q, 
. Dicha integral queda entonces :
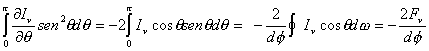, (8.13)
debido a que senq dq = dw/df y 
. Reemplazando (8.13) en (8.12) y teniendo en cuenta que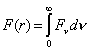 
, resulta :
, (8.14)
la cual puede a su vez escribirse como :
,
F(r) = a/r2 , (8.15)
siendo a una
constante. En una atmósfera extendida en la cual se supone válida la condición
de equilibrio radiativo propiamente dicha, la densidad de flujo de radiación
decae con el cuadrado de la distancia al centro de la estrella.
En las estrellas O, B, A y F, el transporte de energía es esencialmente radiativo, mientras que en las F tardías comienza a ser importante la convección. En las estrellas tardías (K y M) la convección prevalece. Si llamamos f(x) al flujo convectivo, la primera condición de equilibrio radiativo para el caso general se escribirá de la siguiente manera :
div y(x)
= 0, (8.16)
en la cual y(x)
= F(x) + f(x).
El resultado de que el flujo
total F(x) es constante a cualquier profundidad en atmósferas planas y no
extendidas, no puede extenderse de ninguna manera al flujo monocromático Fv, el cual en general varía
con la profundidad.
1.2 Ecuación de continuidad
La segunda condición de equilibrio radiativo resulta de integrar en todas las frecuencias y en todos los ángulos sólidos la ecuación del transporte (7.12). Escribiendo esta ecuación de la siguiente manera :
, (8.17)
e integrando
sobre 4p estereorradianes, se obtiene :
,
en la cual hemos
supuesto que kvr es
independiente de la dirección. Además, si la función fuente Sv tampoco depende de la dirección q resulta :
en la cual hemos
tenido en cuenta la definición de Jn.
Al integrar sobre todas las frecuencias se anula el primer miembro de la expresión anterior, resultando en consecuencia :
, (8.18)
conocida como ecuación de continuidad. Esta expresión
es una consecuencia de la condición de equilibrio propiamente dicha y
constituye la segunda condición de equilibrio radiativo. Su interés principal radica en el hecho de que en ella no
interviene el valor del flujo constante.
Si la función fuente que aparece explícitamente en (8.17) tuviese la forma dada en (6.62), la ecuación de continuidad podría reescribirse de la siguiente manera :
,
la cual se
reduce a la expresión :
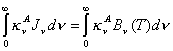
En la igualdad anterior se han cancelado los términos que contienen 
. Esto es físicamente razonable en virtud de que el fenómeno
de dispersión quita y agrega la misma cantidad de energía a un rayo luminoso.
8.1.3
Equilibrio radiativo y presión de radiación
Hemos mostrado que la condición de equilibrio radiativo propiamente dicha (8.1) implica la constancia del flujo total a cualquier profundidad en una atmósfera no extendida. Asimismo, hemos mostrado que en cualquier punto de una atmósfera en equilibrio radiativo tiene validez la ecuación de continuidad (8.18). Veremos ahora qué condición impone el equilibrio radiativo a la presión de la radiación.
Multiplicando la (8.17) por cosq e integrando sobre todos los ángulos sólidos, se obtiene :
Por otra parte, si se tiene en cuenta la definición de integral K dada en (6.29) y la relación (6.10), resulta :
(8.19)
Dividiendo ambos miembros por -kvr,
integrando en todas las frecuencias y teniendo en cuenta que la integral en
(8.19) es nula, resulta :
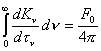, (8.20)
en la cual hemos
hecho uso de la constancia del flujo total integrado a cualquier profundidad.
La expresión (8.20) se conoce como tercera condición
de equilibrio radiativo e impone una condición
a la presión de la radiación.
En síntesis, la condición de equilibrio radiativo propiamente dicha (8.1) implica básicamente tres condiciones. La primera, representada por las expresiones (8.7) u (8.8), se relaciona con el flujo total. La segunda, ecuación de continuidad (8.18), impone una condición a otro parámetro fundamental del campo radiante : la intensidad media. Finalmente, la tercera representada por la expresión (8.20), impone una condición a la presión de la radiación.