Introducción al
Equilibrio Estadístico
Si no hay LTE y la
excitación, ionización y función fuente no están dadas por Boltzmann, Saha y
Planck debemos calcular la población de los niveles involucrados en forma
directa, usando las condiciones del equilibrio estadístico.
Podemos decir que en
equilibrio estadístico la tasa de ocurrencia de los procesos que producen
el poblamiento de un nivel debe ser igual a la tasa de ocurrencia de todos los
procesos que despueblan dicho nivel.
Supongamos un proceso entre
un nivel i y otro j. Ese proceso produce transiciones desde el nivel i al j. La
tasa de dicho proceso se define como el número de transiciones por unidad de
tiempo desde i a j a través de dicho proceso y por partícula en el nivel i.
Esas transiciones pueden
ser procesos radiativos o colisionales Llamamos a los procesos radiativos
(Rij) y a los colisionales (Cij).
De manera que el número de
transiciones por segundo desde i a j por unidad de volumen es
donde Ni es el
número de partículas por unidad de volumen en el nivel i y además siempre
consideraremos que j es el nivel superior.
La condición de EE nos
indica que la población de los niveles debe ser estable de manera que el número
de transiciones que despueblan i debe ser igual al número de transiciones que
pueblan i.
O sea que,
donde obviamente las
sumatorias excluyen i=j.
Habrá ecuaciones similares
para cada nivel i. Deben resolverse simultáneamente teniendo en cuenta la condición que
donde N será el número
total de partículas involucradas.
Las sumatorias incluyen los
diferentes estados de ionización que será necesario considerar. Los estados de
ionización los designaremos con k.
Procesos a considerar
Radiativos
Emisión espontánea: átomo (j) átomo(i) + fotón.
Absorción: átomo(i) + fotón átomo (j)
Emisión estimulada: átomo (j) + fotón átomo(i) + fotón + fotón
La energía del fotón es
siempre Eij = hn .
Colisionales
Excitación: átomo(i) + partícula colisionante
(Eb) átomo
(j) + partícula colisionante (Ef).
En este caso tiene que
ocurrir que E = E + E .
Desexcitación donde la partícula colisionante
sale de la colisión con más energía . En las atmósferas estelares la mayor
parte de las excitaciones colisionales son producidas por electrones.
Transiciones ligado
libre.
Fotoionización: átomo + fotón ión + electrón
En este caso el fotón debe
tener una energía hn mayor que la energía de ionización
necesaria para ionizar el átomo.
Recombinación radiativa: ión + electrón átomo + fotón
Este proceso involucra una
colisión. La energía del fotón hn debe ser igual a c más la energía cinética del
electrón que colisiona de manera que la frecuencia del fotón puede tener
cualquier valor más grande que c /h.
También puede haber
ionización colisional pero en este caso el proceso inverso será la recombinación de tres cuerpos:
Ión +electrón + electrón átomo + electrón
Estos últimos procesos son
despreciables en las atmósferas estelares, pero la ionización colisional puede
ser muy importante en los medios con muy alta temperatura como las coronas
estelares.
Tasas Radiativas
El coeficiente de Einstein
para emisión espontánea desde el nivel j al i es Aji. Se define como
la probabilidad por segundo que un átomo en el nivel j decaiga al i.
El número de decaimientos
radiativos espontáneos desde j a i por unidad de volumen es Nj Aji,
donde Nj es el número de partículas en el nivel j por unidad de
volumen.
Valor típico 10-8
s-1 .
El coeficiente de absorción
de Einstein lo definimos igualando la probabilidad de una transición radiativa
del nivel i al j por unidad de tiempo en un campo de radiación de intensidad
media Jn a 4p Jn Bij donde
= Eij /h siendo Eij la diferencia de energía entre
los niveles.
Surge entonces que,
La probabilidad de
absorción radiativa por segundo por átomo en el nivel i expuestos a una
intensidad In en el
ángulo sólido dW es Bij
In dW . El
coeficiente de Einstein para emisiones estimuladas desde el nivel j al nivel i,
Bji , es definido de la misma forma igualando la probabilidad de un
decaimiento radiativo estimulado desde j a i por unidad de tiempo en un campo
de radiación de intensidad media Jn para la frecuencia de la transición,
a 4p Jn Bji .
Sabemos por resultados de
la mecánica cuántica que la relación entre los coeficientes de Einstein es:
Los g son los pesos
estadísticos.
Las tasas radiativas ahora
las podemos escribir así:
Podemos expresar los
coeficientes de emisión y de absorción en función de los coeficientes de
Einstein.
El coeficiente de emisión j
se define como la energía emitida dentro del ángulo sólido por unidad de masa.
El coeficiente de Einstein se refiere al número de transiciones en todo el
espacio y por lo tanto debemos dividirlo por el ángulo sólido de todo el
espacio y multiplicarlo por la energía de un fotón para reproducir el
coeficiente de emisión.
donde es la densidad de
masa y N es el número de átomo que emiten por unidad de volumen. La emisión
estimulada, como la absorción, es proporcional a la intensidad y por lo tanto
es conveniente incluir la emisión estimulada como una absorción negativa. El
coeficiente de absorción se refiere a la energía absorbida por unidad de masa
de manera que nuevamente los coeficientes de Einstein deben ser multiplicados
por la energía del fotón para obtener el coeficiente de absorción pero en
nuestra definición ellos ya están referidos a una intensidad media y por lo
tanto el factor 4p ya está
incluido.
Los coeficientes de
Einstein se refieren al efecto integrado sobre el perfil de la línea. Si
queremos dar el coeficiente de emisión y absorción en una frecuencia particular
sobre ewl perfil de una línea debemos multiplicar por el perfil de la línea.
donde el perfil está
normalizado.
La función fuente está definida
como la emisión sobre la absorción.
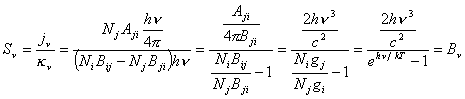12.5
que es la función de Planck
si
con Eij = hn.
o sea si Boltzmann vale.
Por lo tanto cuando no hay
LTE regresamos a la 12.5
(
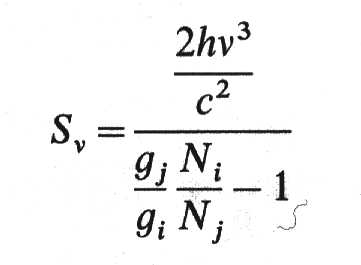12.1)
Estas poblaciones
están determinadas por transiciones colisionales y radiativas entre los niveles
i y j y también por transiciones radiativas hacia otros niveles.
Requerimos que en un estado
estable que la población de cada nivel sea constante en el tiempo.
Podemos combinar las tasas
de todas las transiciones desde el nivel i al j llamándola Pij y por
lo tanto tendremos
(12.2)
esto vale para cada nivel
j.
El término Ni Pij
representa el número de átomos que arriban al nivel j desde el nivel i mientras
que el término Nj Pji representa el número de átomos
perdidos por el nivel j.
Las sumatorias deben
hacerse sobre todas las combinaciones posibles de niveles. Incluyendo el
continuo.
Las tasas de transición Pij
y Pji incluyen como hemos dicho tasas radiativas y colisionales.
donde A = 0 para i < j .
Similarmente podemos
escribir
y
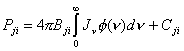para i > j
Este sistema de M-1
ecuaciones debe ser resuelto simultáneamente para los M-1 valores de Nj
y por lo tanto habrá M-2 relaciones independientes porque las ecuaciones están
igualadas a cero. Se resuelven para la razón de las poblaciones y con eso es
suficiente para determinar la función fuente.
Es fácil ver de las
ecuaciones 12.1 y 12.2 el problema de acoplamiento al que hemos hecho
referencia.
Para calcular Sn necesitamos la razón entre la
población de los niveles, pero para calcularlos necesitamos Jn y para calcular Jn es necesario conocer Sn
Los dos procesos físicos que
intervienen en los coeficientes de absorción y emisión son absorción y
dispersión.
Si en la dispersión no hay
corrimiento en longitud de onda o frecuencia entonces el scattering es
coherente.
La función fuente para el
caso de scattering coherente es la intensidad media. Es difícil que haya
scattering coherente., porque los átomos y iones están en movimiento y como la
dirección del fotón dispersado es arbitraria, el corrimiento Doppler es
diferente para el fotón inicial y para el dispersado y esto destruye la
coherencia. Si toda la coherencia es destruida el scattering se denomina
no-coherente y la función fuente correspondiente será
El caso más aproximado es
el de coherencia parcial que fue investigado por Freire Ferrero en 1987
(Ap.J.314,822).
En general tanto el
scattering como la absorción verdadera están presentes en la formación de las líneas.
Jefferies en 1968 (Spectral Lines formation. Blaisdell:Waltham) determinó que la función
fuente para un átomo de dos niveles podía escribirse así:
(12.3)
donde e(tn) está relacionado con la razón
entre las desexcitaciones colisionales y la desexcitaciones espontáneas. Cuando
e(tn) es pequeño el scattering domina ty
hay grandes desviaciones del LTE .
En capas profundas donde la
profundidad óptica es grande para todas las frecuencias la función fuente se
transforma en la ley de Planck.
En las capas más
superficiales e(tn)
se hace más pequeño porque las desexcitaciones colisionales se hacen menos
probables al disminuir la densidad. Dependiendo del valor de e(tn) hay una profundidad sobre la cual
el término de scattering domina a la 12.3.
Cuando vamos cada vez más arriba
en la atmósfera estaremos cada vez más cerca de la frontera donde la estrella
pierde fotones. La pérdida de fotones significa que la intensidad media decrece
con la altura y por lo tanto también decrece la función fuente y como hemos
visto esta es la causa de que exista un línea de absorción.
Una línea intensa se forma
sobre un amplio rango de profundidad. Las alas en las capas más profundas y los
núcleos en las capas más superficiales. Debemos esperar que las alas se formen
en LTE y sean controladas por Planck mientras que los núcleos se formarán en
non LTE y su forma estará controlada por el decrecimiento de la intensidad
media Para la línea D del Sodio en el
Sol ocurre esta situación y el límite entre los dos casos es Dl= 0.2 A.
Obviamente los átomos
tienen más de dos niveles y hay otros cálculos que llevan a formas más
complejas.