Formación de Líneas
espectrales
Predicción del Espectro
emergente
En general para
profundidades ópticas medidas a los largo de la línea de la visual

En una atmósfera de capas
planas y paralelas

El flujo emitido será

y el flujo recibido de una
estrella esférica de radio R a una distancia d es:

Los datos para predecir el
espectro emergente son: la función fuente y el coeficiente de absorción.
El coeficiente de absorción
a una frecuencia dada es la suma de los coeficientes de todas las líneas que
tengan una intensidad significativa para esa frecuencia y el del continuo, que
no varía prácticamente sobre la línea.

Cada línea está definida
por el nivel superior j, nivel inferior i y fuerza del oscilador fij.
Consideramos una línea sola pero recordemos que en general hay superposición.
También recordemos que N en
general no surge de Boltzmann y Saha como en LTE.
En una atmósfera estelar se
expresan las variables en función de una profundidad óptica que corresponde a
un coeficiente de absorción para una frecuencia standard (5000A).Llamamos ks al coeficiente de absorción del continuo para
la frecuencia standard y ts es
la correspondiente profundidad óptica.
Luego

Mayor problema: función
fuente.
Si vale LTE entonces la
función fuente es Planck tanto para el continuo y para la línea. En
general no es el caso y las dos funciones fuentes son distintas.
O sea,

Existen métodos para
calcular la función fuente cuando no hay LTE.
Si medimos la profundidad
en cada punto de la línea por:

La profundidad valdrá entre
0 y 1.
La intensidad total de la
línea se expresa normalmente en la forma de ancho equivalente, y está dada por:

La profundidad en el centro
de la línea también es un parámetro que suele darse al igual que el ancho de la
línea a mitad de profundidad.
Podemos predecir los anchos equivalentes usando algunas aproximaciones.
Aproximación de Schuster-Schwartzschild
Si tenemos una nube con
función fuente S1 uniforme, espesor h en la línea de la visual y
densidad r, que interactúa con radiación sólo a longitudes de onda de líneas y es iluminada
por una fuente continua pequeña de intensidad IC con IC
> S1

El ancho equivalente en el
espectro de intensidad es:

La profundidad central de
la línea es,

Para una línea intensa
será:
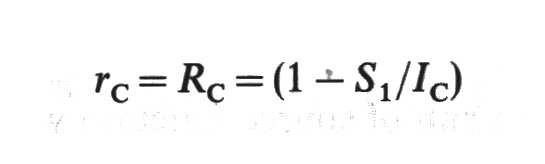
RC es la máxima
profundidad posible en la líinea
La ecuación que da W se
puede escribir,

con el miembro izquierdo
sin dimensión
Para una línea débil
1-e-t ~ t
si t << 1 aun en el centro de la línea
entonces,

Llamamos
![]()
donde k’0 es el coeficiente de absorción.
Reemplazando la expresión
para el coef. de absorción de la línea
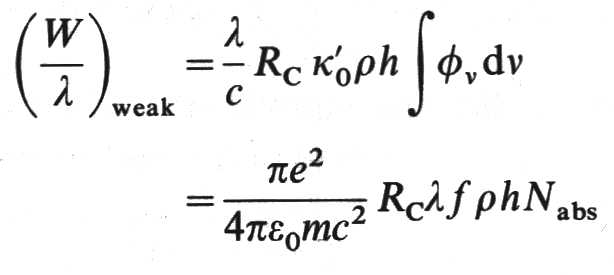
ya que la integral
vale 1 (perfil normalizado).
El rasgo importante en la
formación de líneas es que en las frecuencias de una línea la radiación
observada proviene de capas más superficiales de una estrella y si la función
fuente decrece hacia fuera la radiación emitida será menor que en las
frecuencias vecinas dando origen a una absorción.
Aproximemos la atmósfera
por dos capas. La capa mas profunda tiene función fuente S2
Y produce el continuo. La
mas superficial tiene S1
y se extiende desde t = 0 a t = tL
sólo el coeficiente de
absorción de línea es significativo..
entonces,

La profundidad óptica se
asume medida perpendicularmente a las capas planas y paralelas.
Luego la profundidad en la
línea es,
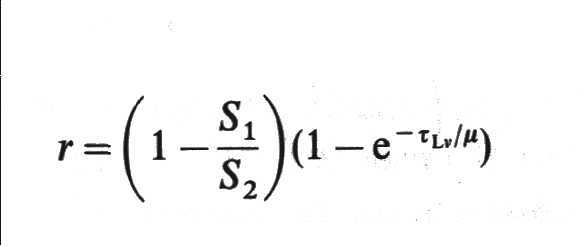
y es lo mismo que obtuvimos
más arriba si reemplazamos IC = S2
Lo que hemos hecho en
efecto es que la variación continua de la función fuente con la profundidad la
hemos aqproximado por dos capas con el punto de división en la profundidad geométrica
x elegida de manera que
![]()
sea
considerablemente menor que 1. Supongamos que sea igual a q. Entonces
![]()
de
manera que la profundidad óptica representa la razón entre la absorción de la línea
y del continuo.
Indica
que es importante el contraste .
Para una línea débil
obtenemos igual que anteriormente,

Esta clase de aproximación
se denomina de Schuster- Schwartzschild.
Podemos expresar en función
del flujo,

Hemos reemplazado usado las propiedades de las integrales
exponenciales.
Luego,

Este modelo es muy grosero y es una aproximación muy cruda. La función fuente, la temperatura en las estrellas reales presentan variaciones continuas con la profundidad.
Aproximación
de Milne-Eddington
Más realista es Milne-Eddington. Se supone un cociente constante entre el coeficiente de absorcion de la línea y del continuo con la profundidad. (kL/kC)=hn También se supone que la función fuente es lineal con la profundidad óptica del continuo. S = a + btc.
Luego en la linea,

Para longitudes del
continuo tendremos,

Para longitudes de la línea
tendremos,

El ancho equivalente de la
línea en flujo es,

La máxima profundidad
central posible para una línea intensa es 2b/(3a + 2b)= RC y podemos escribir entonces, el ancho
equivalente sin dimensión:
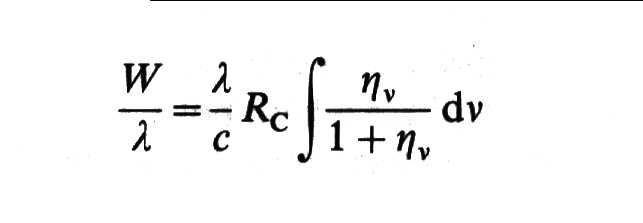
En el caso de líneas
débiles h << 1 tendremos:

Las atmósferas reales no
tienen funciones fuentes que dependan linealmente de la profundidad óptica.
Además las funciones fuente del continuo y las líneas varían en forma distinta
con la profundidad, es decir con T y P, pero para líneas débiles cuya
profundidad de formación es parecida a la del continuo la última expresión
funciona bien.
Es costumbre agrupar el
peso estadístico g con f y además se suele expresar el coeficiente de
absorción del continuo como el producto de la sección transversal por átomo de
H para la absorción continua y el número de átomos de H por unidad de masa
Obtenemos,
 (12. 5)
(12. 5)
El término constante vale
8.85 x 10-15m. Si vale LTE, Rc es fijo para una estrella
dada y ac
es una función de la
temperatura y presión en la capa de formación del continuo y que varía
lentamente con la longitud de onda.
Supongamos que el perfil de
una linea es gaussiano,

Luego,

Expandiendo la exponencial
en serie de potencias,
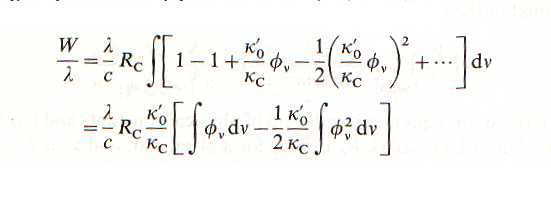
en primer orden.
Sustituyendo

Si u = ![]()

El primer término representa
una curva de crecimiento lineal y por lo tanto los apartamientos de la
linealidad se hacen significativos cuando

o sea cuando

Si usamos el modelo de
Milne-Eddington
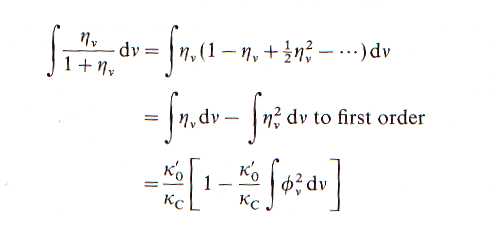
Para una estrella de tipo
solar para long. de onda 5000A con ancho Doppler 0.003 nm y R=0.5 aún una línea
con ancho equivalente de 0.00037 nm muestra incipiente saturación
Para líneas más intensas

Si sustituimos en el modelo
de Schuster-Schwartzschild la intensidad en el centro del disco
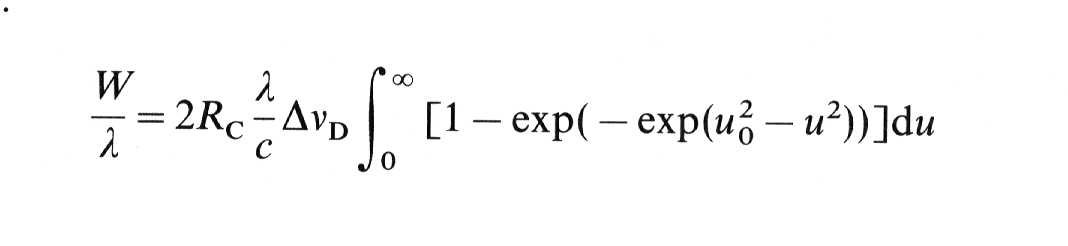
Un resultado similar se
obtiene de ME.
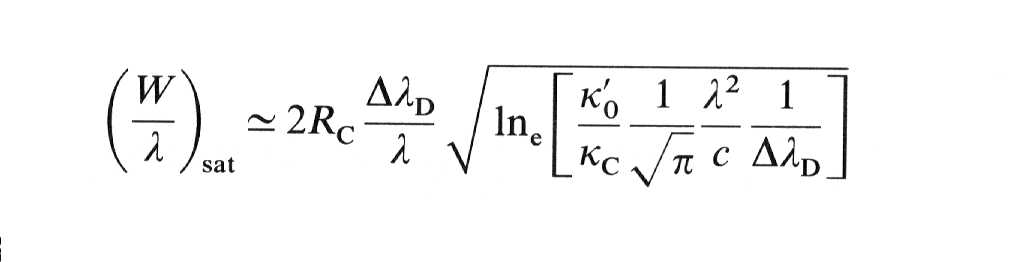

En el caso que el ancho
equivalente pueda ser hallado aproximadamente suponiendo que la línea tiene un
perfil Lorentziano,
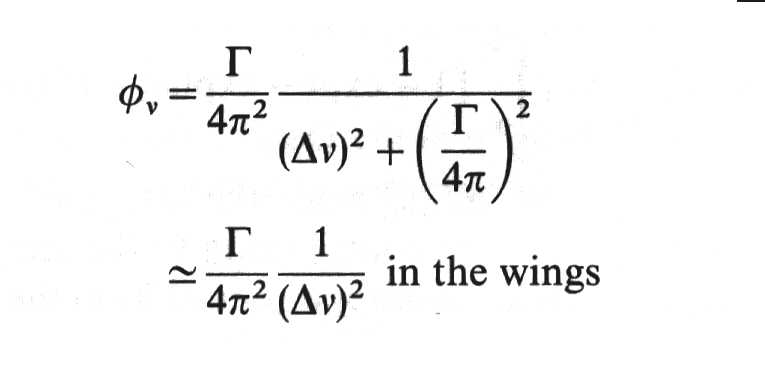
El modelo SS para el centro
del disco da:

La integral puede
escribirse,

Luego
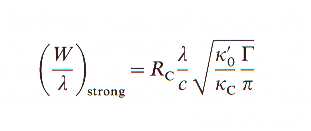
El ME da similarmente,

Esto da lugar a la
denominada porción de amortiguamiento de la curva de crecimiento. el ancho
equivalente ahora aumenta con la raíz cuadrada de lgfN/N pero también depende de la raíz cuadrada de
