6 MÉTODO DE LAS ORDENADAS DISCRETAS DE CHANDRASEKHAR
6.1 Fundamento del método
Además de las aproximaciones de
Eddington descriptas en las secciones precedentes, existen otras aproximaciones
válidas para el caso gris y equilibrio radiativo. Entre éstas, la de mayor
precisión es sin lugar a duda la aproximación desarrollada por Chandrasekhar
(1944, 1960). El principio del procedimiento usado por este autor fue
originalmente introducido por Wick (1943), en relación con un problema de
difusión de neutrones en una pila. Dado que una descripción completa y
detallada del método de las ordenadas discretas involucra una gran cantidad de
desarrollos matemáticos, sólo describiremos acá la idea general del método para
conocer en qué consiste básicamente esta aproximación.
Para resolver la ecuación del
transporte radiativo (9.1) válida para la atmósfera gris, Chandrasekhar
introdujo el siguiente cambio de variables : m = cosq, dm
= -senq dq. Con esta sustitución, la función fuente integrada
![]()
se
transforma en :
 (9.80)
(9.80)
El método tiene por objeto hallar la intensidad I(t,m) que sea solución de la siguiente ecuación integro-diferencial de transporte radiativo :
![]() (9.81)
(9.81)
Un principio fundamental del método
de Chandrasekhar consiste en expresar la integral de (9.81) como una suma de
intensidades pesadas por ciertos factores, teniendo en cuenta una fórmula de
integración numérica debida a Gauss (fórmula
de cuadratura de Gauss). Esto permite reducir la ecuación (9.81) a un
sistema de ecuaciones diferenciales lineales para las intensidades en ciertas
direcciones correspondientes a los puntos de subdivisión del rango de
integración (-1,+1) de la variable independiente m. Si dicho rango se divide en m puntos mj, simétricamente espaciados respecto del punto medio
m = 0, entonces Gauss ha mostrado que la integral de
(9.81) puede aproximarse por la sumatoria siguiente :
![]() (9.82)
(9.82)
en la cual
cada uno de los puntos mj es un cero o
solución del polinomio de Legendre de
grado m, Pm(m). Puede mostrarse que los factores de peso Aj están dados por :
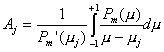 (9.83)
(9.83)
Un resultado importante que debemos
mencionar es que la suma Gaussiana de (9.82) reemplaza exactamente la integral de I(t,m) siempre que I(t,m) se
escriba como un polinomio en la variable m de grado
menor o igual que 2m-1.
Resulta conveniente usar en (9.83) los polinomios de
Legendre de orden par P2n(m) con los 2n ceros o soluciones m-n,
m-(n-1),
....,m-1,
m1,
m2,
...., mn. Los m puntos mj en que se dividió antes el intervalo de integración
de la variable independiente, equivalen ahora a los 2n puntos m-n,
m-(n-1),
....,m-1,
m1,
m2,
...., mn (Figura 9-8). Con
esta particular subdivisión del intervalo (-1,+1) de la variable m, la fórmula de cuadratura de Gauss se
escribe de la siguiente manera :
![]() (9.84)
(9.84)
en la cual
no se incluye el término j = 0. Los
factores de peso Aj
se conocen como los números de Christoffel.
Dado que la variable dependiente Ij(t,mj) es
simétrica con respecto a m, los
coeficientes Aj verifican
la importante propiedad :
Aj
= A-j (9.85)
Asimismo, puesto que m
= cosq y mj es un ángulo simétrico respecto de m-j (Figura 9-8), se
verifica que :
mj = -m-j, (9.86)
ya que si
dos ángulos son simétricos, las funciones trigonométricas de uno son iguales en
valor absoluto y signo contrario a las funciones del otro, con excepción del
seno y la cosecante que tienen el mismo signo.
La representación (9.84) de la
integral
![]()
como una suma
finita puede ser tan precisa como se desee eligiendo el valor de n suficientemente grande. Precisamente,
Chandrasekhar denomina aproximación
n-ésima al proceso de subdivisión del rango de integración de la variable
independiente en 2n puntos mj, simétricamente
espaciados respecto de m = 0. La ecuación integro-diferencial (9.81) del caso
gris se reemplaza ahora por un conjunto de 2n
ecuaciones diferenciales, cada una de las cuales representa una ecuación
lineal para la intensidad específica integrada en la dirección correspondiente
al cero mi del
polinomio de Legendre P2n(m). El sistema lineal de ecuaciones
diferenciales para la intensidad en las 2n direcciones mi es :
![]() (9.87)
(9.87)
en el cual
el subíndice i toma los valores ±1, ±2, ..., ±n. Los valores positivos del subíndice i corresponden a intensidades emergentes
en las n direcciones mi, en tanto que los valores negativos de i corresponden a las intensidades
entrantes en las n direcciones –i (Figura 9-8).
Una vez conocida la solución general
del sistema (9.87), podremos calcular la función fuente integrada
![]()
en la n-ésima aproximación de Chandrasekhar y,
usando las ecuaciones (7.25) y (7.26), será posible calcular la intensidad
específica integrada I(t,m) en cualquier dirección. Éste es pues
el fundamento del método.
6.2 Solución general del sistema de ecuaciones diferenciales
Para resolver el sistema de ecuaciones simultáneas (9.87) obtendremos primero las diferentes soluciones linealmente independientes del mismo, las cuales serán luego combinadas para obtener la solución general. Como el sistema de 2n ecuaciones diferenciales es lineal y de primer orden, probaremos una solución exponencial en t de la forma :
![]() , (i
= ± 1,..., ± n) (9.88)
, (i
= ± 1,..., ± n) (9.88)
en la cual gi,a y ka son constantes a determinar. El
significado del subíndice a
resultará evidente más adelante.
Sustituyendo (9.88) en (9.87)
obtenemos :
![]() (i = ± 1, ..., ± n) (9.89)
(i = ± 1, ..., ± n) (9.89)
Como el segundo miembro de esta
expresión no depende del subíndice i,
es una constante independiente de i a
la que denotaremos Ca. Luego :
![]() (i = ± 1, ..., ± n) (9.90)
(i = ± 1, ..., ± n) (9.90)
Reemplazando (9.90) en (9.88) y a su
vez este valor en (9.87) resulta :
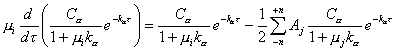 ,
,
la cual se
reduce a la siguiente ecuación de autovalores en ka
:
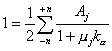 (9.91)
(9.91)
Si en (9.91) se desarrollan
solamente los términos ± j con j = 2,
se tiene :
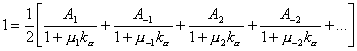 ,
,
y
utilizando las propiedades (9.85) y (9.86) se advierte que la ecuación (9.91)
es equivalente a la expresión :
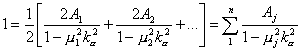 ,
(9.92)
,
(9.92)
conocida
como ecuación característica.
Llegamos entonces a la conclusión de que si (9.88) es una solución general del sistema
(9.87), entonces ka debe satisfacer la ecuación algebraica
(9.92). Por otra parte, si se desarrollan los n términos de (9.92) y se
multiplican ambos miembros de la ecuación por
![]() ,
,
dicha expresión es equivalente a un polinomio de
grado n, Pn(x), en la
variable ![]() . En consecuencia, deben existir n raíces o soluciones
. En consecuencia, deben existir n raíces o soluciones ![]() , con a
= 1, 2, ...n, de este polinomio. Nótese que
cada una de estas ráices es de multiplicidad
doble, de manera que es legítimo aseverar que la ecuación caracterísitca
(9.92) tiene 2n raíces de multiplicidad simple de la forma ±
ka,
con a = 1,
2, ...n. Se aprecia ahora claramente el motivo por el que se introdujo el
subíndice a. En
efecto, el mismo permite distinguir los n
valores diferentes de k2
que satisfacen la ecuación característica.
, con a
= 1, 2, ...n, de este polinomio. Nótese que
cada una de estas ráices es de multiplicidad
doble, de manera que es legítimo aseverar que la ecuación caracterísitca
(9.92) tiene 2n raíces de multiplicidad simple de la forma ±
ka,
con a = 1,
2, ...n. Se aprecia ahora claramente el motivo por el que se introdujo el
subíndice a. En
efecto, el mismo permite distinguir los n
valores diferentes de k2
que satisfacen la ecuación característica.
¿ Cuáles son los n
valores diferentes de ![]() (a
= 1, 2, ...n) que satisfacen la ecuación (9.92)
? De estas n raíces o soluciones una
es relativamente simple de encontrar, la denominada solución trivial
(a
= 1, 2, ...n) que satisfacen la ecuación (9.92)
? De estas n raíces o soluciones una
es relativamente simple de encontrar, la denominada solución trivial ![]() . En efecto, dado
que
. En efecto, dado
que
![]()
y en el esquema
de las ordenadas discretas es
![]() ,
,
entonces :
![]() , (9.93)
, (9.93)
o bien,
como Aj = A-j,
la (9.93) implica que
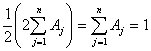 , expresión ésta que satisface la ecuación característica
(9.92) para
, expresión ésta que satisface la ecuación característica
(9.92) para ![]()
La solución
trivial representa entonces sólo una de las n raíces o soluciones de multiplicidad doble de la ecuación
característica (9.92), o bien dos de las 2n
raíces o soluciones de multiplicidad simple de dicha ecuación. De aquí que
(9.91) o su similar (9.92) permitirán encontrar las 2n-2 raíces distintas de
cero para los pares de valores ± ka, siendo a = 1, 2, ...n-1.
La solución general del sistema de
ecuaciones diferenciales (9.87) debe ser la combinación lineal de las (2n-2) soluciones linealmente
independientes - correspondientes a las (2n-2)
raíces diferentes de cero ±ka, con a = 1, 2, ...n-1 – más una solución particular de (9.87) que corresponda a
la raiz ![]() . Teniendo en cuenta (9.88) y (9.90), la solución general para
las (2n-2) soluciones linealmente
independientes será :
. Teniendo en cuenta (9.88) y (9.90), la solución general para
las (2n-2) soluciones linealmente
independientes será :
![]() (9.94)
(9.94)
con i = ±1, ±2, ..., ±n.
Debemos buscar ahora una solución
particular del sistema (9.87) correspondiente a la raiz ![]() , para lo cual
ensayamos una solución lineal en t de la siguiente forma :
, para lo cual
ensayamos una solución lineal en t de la siguiente forma :
![]() , (9.95)
, (9.95)
con i = ±1, ±2, ..., ±n y en la que b
es una constante a determinar. Introduciendo esta solución en (9.87) resulta :
![]() (9.96)
(9.96)
Teniendo en cuenta la (9.93), la
expresión anterior queda :
![]() (9.97)
(9.97)
Como el segundo término del segundo
miembro no depende del subíndice i,
es simplemente una constante independiente de dicho índice, a la que
Chandrasekhar denota Q. La solución
(9.95) ensayada debe ser entonces de la forma :
![]() (9.98)
(9.98)
Combinando (9.94) y (9.98),
soluciones linealmente independientes de (9.87), se obtiene la solución general
del sistema (9.87) :
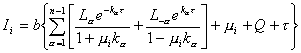 , (i = ±1,..., ±n)
(9.99)
, (i = ±1,..., ±n)
(9.99)
en la cual b, Q,
La
y L-a
son 2n constantes de integración.
6.3 Condiciones de contorno
Debemos especificar ahora los 2n coeficientes desconocidos b, Q
y L±a (a = 1, 2, ..., n-1),
para lo cual aplicaremos las condiciones de contorno. Recordemos en primer lugar que de una atmósfera
semi-infinita no puede emerger radiación proveniente de capas infinitamente
profundas. Es decir, dicha atmósfera debe verificar la condición de contorno (7.14)
:
lim I(t,m) e-t/m = 0,
t®¥
en la cual m
= cos q. Si al tender la profundidad t a infinito, I(t,m) no puede diverger exponencialmente, entonces las (n-1) constantes de integración L-a (a = 1,
2,..,n-1) deben anularse. La
solución (9.99) queda entonces :
![]()
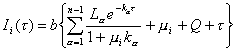 (9.100)
(9.100)
Por otra parte, la constante Q y las (n-1) constantes de integración La (a = 1, 2, ...n-1) pueden determinarse teniendo en cuenta que en la
superficie de la atmósfera (t = 0) no hay radiación entrante. Esto es equivalente a
aceptar que Ii(0) debe
anularse para los valores de i = -1, -2, ...-n. Si se aplica esta condición de contorno y se utiliza la
propiedad (9.86), la (9.99) da lugar al siguiente sistema de n ecuaciones :
![]() , (i = 1, 2, ..., n) (9.101)
, (i = 1, 2, ..., n) (9.101)
cuyas
incógnitas son precisamente la constante Q
y las (n-1) constantes La (a = 1, 2,
...,n-1).
6.4 Determinación de la constante b
Para determinar la constante de
integración b de (9.100),
Chandrasekhar demuestra primero que esta constante está vinculada al denominado
flujo astrofísico, definido como :
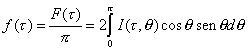 (9.102)
(9.102)
Si se efectúa nuevamente el cambio de variable m
= cosq, dm = -senqdq, la expresión (9.102) resulta
entonces:
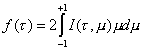 ,
,
y en el esquema de las ordenadas discretas se tiene
:
![]() (9.103)
(9.103)
Reemplazando la solución general
(9.100) en (9.103) se tiene :
 , (9.104)
, (9.104)
O bien :
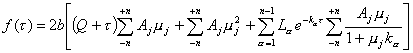 (9.105)
(9.105)
Como en el esquema de las ordenadas discretas es :
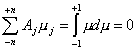 (9.106)
(9.106)
y
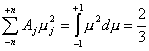 , (9.107)
, (9.107)
el flujo
astrofísico resulta :
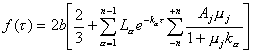 (9.108)
(9.108)
Probaremos a continuación que :
![]() , (9.109)
, (9.109)
para lo
cual desarrollaremos la expresión (9.109), teniendo en cuenta la propiedad
(9.85) :
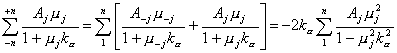 (9.110)
(9.110)
Multiplicando y dividiendo el denominador de la
expresión anterior por ![]() se tiene :
se tiene :
![]() ,
(9.111)
,
(9.111)
en la cual
hemos denotado
![]() y
y ![]() .
.
Definamos ahora una función J(Xa) tal que :
![]() (9.112)
(9.112)
Como (9.93) es equivalente a la expresión ![]() , la función J(Xa)
puede escribirse :
, la función J(Xa)
puede escribirse :
![]() (9.113)
(9.113)
A su vez, como la ecuación
característica (9.92) puede escribirse en la forma :
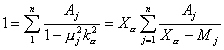 , (9.114)
, (9.114)
al comparar
(9.113) con (9.114) resulta J(Xa)
= 0 y por ende también se anula la expresión (9.112), lo que prueba la
igualdad (9.109). Si se tienen en
cuenta (9.106), (9.107) y (9.109), el flujo astrofísico de (9.105) resulta :
![]() (9.115)
(9.115)
Como hemos mostrado que el flujo
total F(t) es constante a cualquier profundidad y además f(t) = F(t)/p, entonces :
![]() , (9.116)
, (9.116)
en la cual F0 es el flujo total en la
superficie.
La solución completa del sistema de ecuaciones
diferenciales (9.97) es entonces:
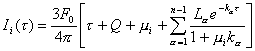 (i
= ±1, ...,±n) (9.117)
(i
= ±1, ...,±n) (9.117)
6.5 Función fuente integrada en la n-esima aproximación
Habiendo encontrado la solución
general de la ecuación (9.87), podemos ahora calcular la función fuente
integrada en la n-ésima aproximación de
Chandrasekhar. De (9.80) y (9.84) se tiene que :
![]() (9.118)
(9.118)
![]()
Reemplazando (9.117) en (9.118)
resulta :
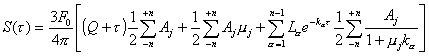 (9.119)
(9.119)
Hemos demostrado ya que
![]()
y
![]() y además de (9.91) se
verifica la siguiente identidad :
y además de (9.91) se
verifica la siguiente identidad :
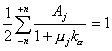 , de manera
que la (9.119) se transforma simplemente en :
, de manera
que la (9.119) se transforma simplemente en :
![]() , (9.120)
, (9.120)
expresión
ésta que suele escribirse en la forma :
![]() , (9.121)
, (9.121)
con : ![]() (9.122)
(9.122)
Chandrasekhar (1960) ha demostrado
que, independientemente de n, es :
![]() , (9.123)
, (9.123)
de manera
que la condición de contorno en la n-ésima
aproximación se escribe como :
![]() (9.124)
(9.124)
Dado que
![]()
en la
primera aproximación de Eddington y
![]()
en la segunda
(incluyendo la aproximación corregida), resulta entonces que :
![]()
6.6 Intensidad específica integrada en
cualquier dirección
Conocida la función S(t) en la n-ésima
aproximación de Chandrasekhar, es posible ahora calcular la intensidad I(t,m) en cualquier dirección m
= cos q,
usando las ecuaciones (7.25) y (7.26). En particular, de (7.25) y (9.120) la
intensidad integrada Iem(t,m) que emerge en la dirección m
desde una capa a profundidad t,
siendo 1³ m ³
0, puede escribirse
como :
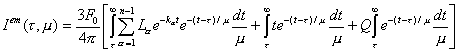 ,
,
la que
puede aún desarrollarse de la siguiente manera :
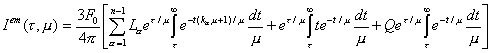 (9.125)
(9.125)
Si se hace la sustitución y =t/m, dy = dt/m, al integrar por partes la segunda
integral de (9.125) resulta :
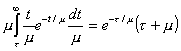 ,
,
en tanto
que la tercera integral de (9.125) es igual a ![]() . Resolviendo ahora la primera integral de (9.125) se
obtiene :
. Resolviendo ahora la primera integral de (9.125) se
obtiene :
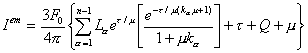
O bien :
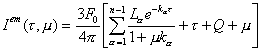 , (9.126)
, (9.126)
válida para
las direcciones emergentes 1 ³
m ³ 0, o bien p/2
³ q ³
0. Nótese que la
expresión obtenida para la intensidad emergente en cualquier dirección, es
exactamente la misma que se obtuvo en (9.117) sin el subíndice i.
Por su parte, la intensidad
integrada entrante Iin(t,-m), con 0 £ m £
1, se calcula de
(7.26) y (9.120) de la siguiente manera :
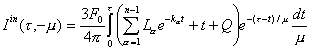 (9.127)
(9.127)
Desarrollando esta ecuación se obtiene
finalmente :
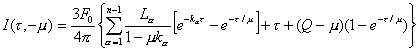 , (9.128)
, (9.128)
con 1 ³ m
³ 0. Nótese que esta expresión no es igual a la
obtenida en (9.117) usando el subíndice –i,
esto es :
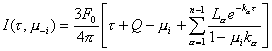 (9.129)
(9.129)
6.7 Ley de oscurecimiento hacia el
borde y distribución de temperatura
La ley de oscurecimiento hacia el
borde en la n-ésima aproximación de
Chandrasekhar se obtiene directamente de (9.127) haciendo t
= 0. De esta manera
resulta :
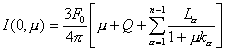 (9.130)
(9.130)
En la Tabla 9-3 se muestran los valores
![]()
obtenidos a
partir del método de las ordenadas discretas de Chandrasekhar con n =1, 2, 3, 4 e infinito.
Para obtener la distribución de temperatura,
el procedimiento es similar al empleado en las dos aproximaciones de Eddington.
Es decir, como pB[T(t)]
= sT4(t), S(t)
= B[T(t)] y
![]()
resulta :
![]() , (9.131)
, (9.131)
en la cual
: ![]() (9.132)
(9.132)
TABLA 9-3 : Oscurecimiento hacia el borde en la aproximación de Chandrasekhar. Los valores tabulados corresponden a
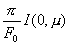 .
.
![]()
cos q 1ª 2ª 3ª 4ª Infinita
0.0 0.4330 0.4330 0.4330 0.4330 0.4330
0.1 0.5080 0.5224 0.5285 0.5319 0.5401
0.2 0.5830 0.6078 0.6164 0.6205 0.6280
0.3 0.6580 0.6905 0.7003 0.7046 0.7112
0.4 0.7330 0.7716 0.7819 0.7861 0.7921
0.5 0.8080 0.8515 0.8620 0.8660 0.8716
0.6 0.8830 0.9304 0.9410 0.9449 0.9501
0.7 0.9580 1.0088 1.0193 1.0231 1.0280
0.8 1.0330 1.0866 1.0970 1.1007 1.1053
0.9 1.1080 1.1640 1.1743 1.1779 1.1824
1.0 1.1830 1.2411 1.2513 1.2548 1.2591
Finalmente, en t = 0 resulta la siguiente relación entre la temperatura efectiva y superficial :
![]() (9.133)
(9.133)