4. LOS ESPECTRÓGRAFOS “ECHELLE”

 

 

 

Los espectrógrafos echelle utilizan redes “echelle” que tiene muchos menos surcos por mm que las redes de los espectrógrafos anteriores. Típicamente tienen entre 50 y 80 l/mm. La red “echelle” se usa en órdenes altos y los ángulos de blaze se encuentran entre 60 ° y 75° aproximadamente. En un espectrógrafo echelle todos los órdenes (típicamente entre el número 25 y 100) se encuentran superpuestos y para aislarlos puede usarse un filtro de banda angosta o más corrientemente un dispersor cruzado que separa todos los órdenes. Se opera en órdenes altos y eso hace que cada orden abarque muy poco en longitud de onda pero la ventaja es que sobre un CCD se registran muchos órdenes simultáneamente. Un ejemplo de configuración de un espectrógrafo echelle se muestra en  la Figura 5-8.

 

 

 

 

 

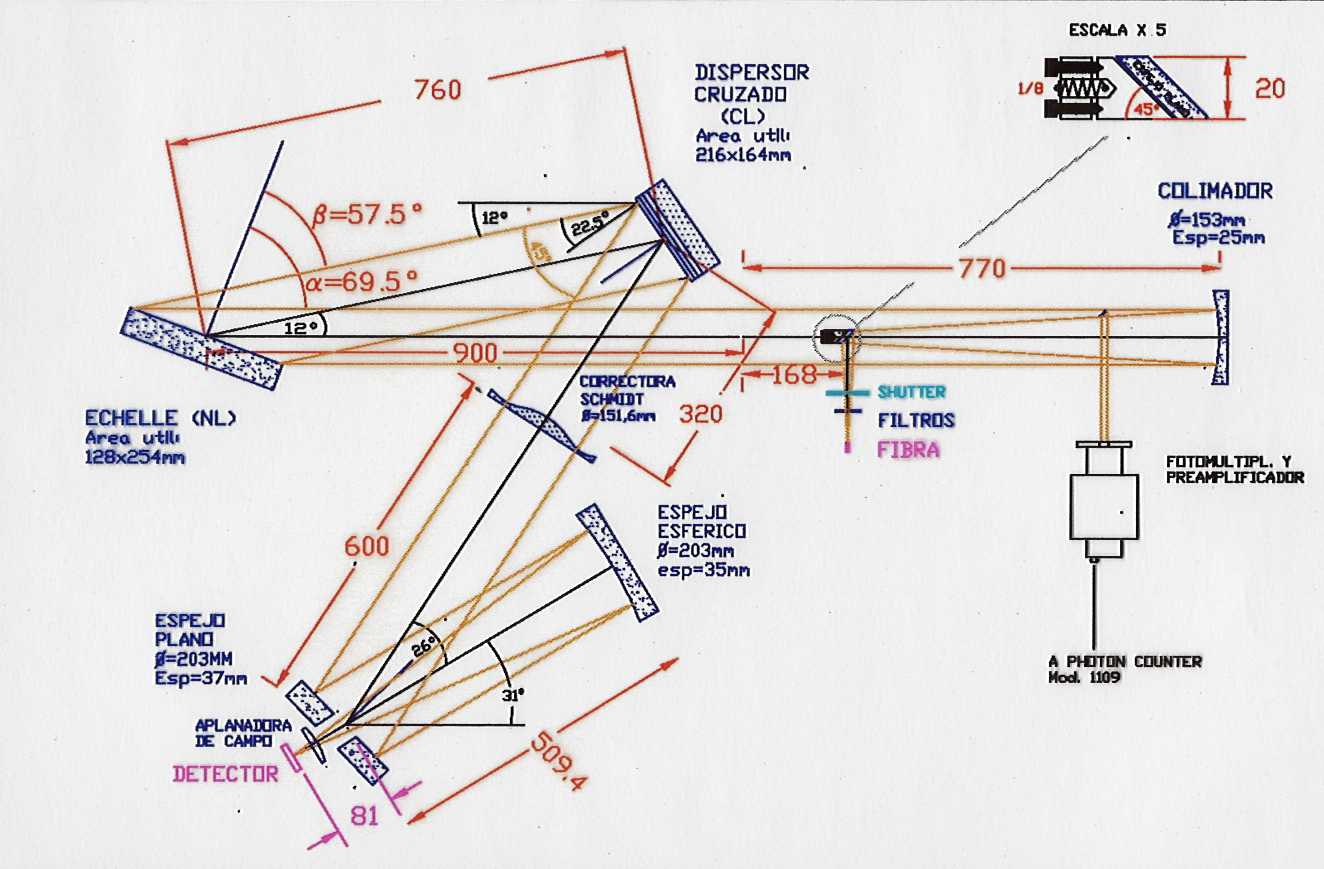
 Figura 5-8. Esquema óptico del  espectrógrafo echelle de banco que se encuentra en CASLEO

El plano del papel es el banco óptico sobre el cual se distribuyen los elementos ópticos tal como muestra la figura.

La fibra óptica en este caso transporta la luz hasta el foco del colimador que tiene una distancia focal de 770 mm. El colimador transforma el haz en paralelo y lo envía a la red echelle que tiene las líneas perpendiculares al banco óptico que está representado como dijimos por el plano del papel. La  echelle  de 31 líneas por mm, produce todos los espectros, uno para cada orden , todos superpuestos. Recordemos que los espectros siempre se dispersan en el sentido perpendicular a los surcos, por lo tanto en este caso todos los espectros de todos los órdenes superpuestos están dispersados paralelos al plano del banco óptico. De allí el haz viaja hacia una red que representa el dispersor cruzado que tiene las líneas paralelas al plano del banco y que tiene por misión separar los diferentes órdenes. Es decir que ahora los espectros de los diferentes órdenes se separan en dirección perpendicular al plano del banco y por lo tanto el formato final será de dos dimensiones.

Una vez finalizado el proceso de dispersión el haz pasa a la cámara Schmidt que tiene su correctora como primer elemento, un espejo plano para doblar el haz y el espejo esférico de la cámara. El Espejo plano tiene un orificio central que deja pasar la luz hasta el detector. Este recoge más de 30 órdenes que han sido separados por el dispersor cruzado.

 

Foto 5-1. El banco óptico con algunos de los componentes el espectrógrafo de banco de CASLEO

 

La Foto 5-1 muestra la ubicación real sobre el banco óptico de los distintos elementos del espectrógrafo echelle de banco de CASLEO. 

Las relaciones matemáticas para una echelle pueden derivarse de las expresiones que ya vimos teniendo en cuenta solamente que la echelle debe trabajar en montaje muy cercano a Littrow pero que por razones prácticas debe separarse el haz incidente del difractado a los efectos de dejar el espacio necesario para colocar la cámara.

 

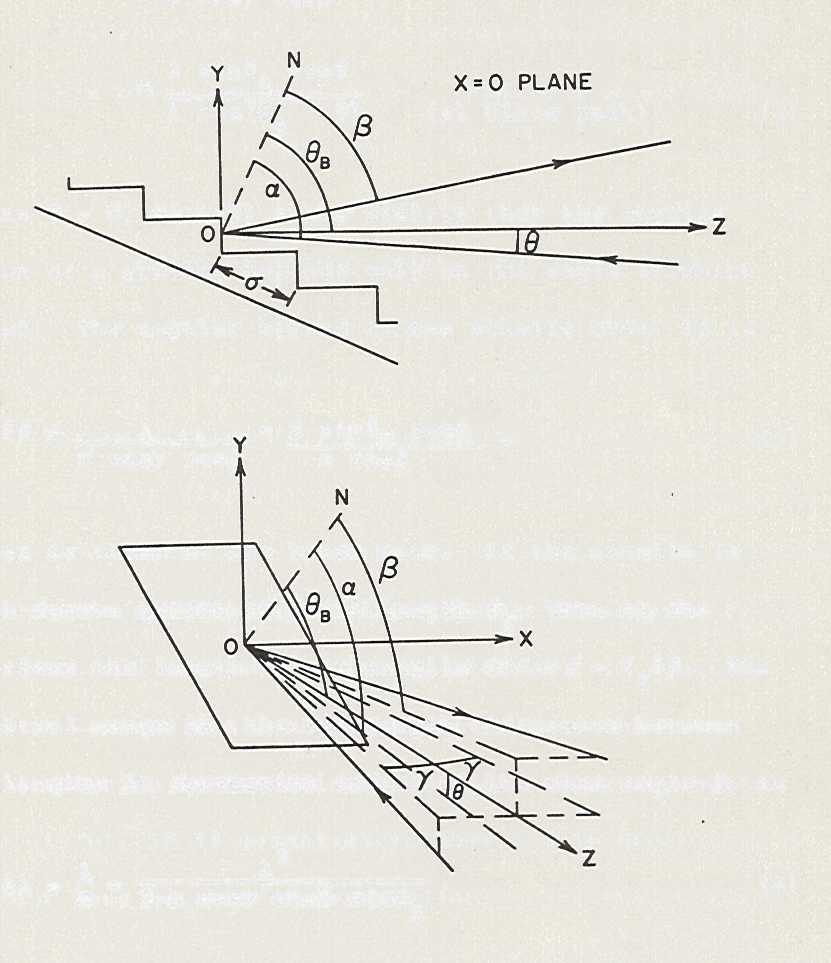
Figura 5-9. Esquema geométrico de los rayos en una red echelle.

 En la Figura 5-9  se muestra el esquema geométrico de los rayos sobre la echelle. El eje x se encuentra a lo largo del surco, el plano y=0 forma un ángulo q_b con la normal a la red echelle o sea formando el ángulo de blaze.. La ecuación de la echelle es:

                                                   (5-32)

 

 

Obsérvese que gamma es el ángulo entre el haz incidente y el plano yz.

De la figura se ve que cuando se trabaja en el pico de máxima eficiencia o sea en el ángulo de blaze:

                                                                                                             (5-33)

 

donde usamos que a-q_b  = q    y   q_b - q = b

La dispersión angular se obtiene diferenciando la 5-32 y será:

 

                                                                                                                      (5-34)

Esto es en el pico del blaze 

Si reemplazamos m/a  por la 5-32 y los ángulos a y  b por las expresiones anteriores obtenemos

                                                                                                                      (5-35)

 

donde hemos utilizado las igualdades trigonométricas entre las suma y diferencia de dos ángulos.

Si tomamos q = 0 la ecuación anterior nos muestra claramente que la dispersión angular de una red depende sólo del ángulo bajo el cual se utiliza. Recordando la 5-2,  la dispersión en Å/mm si la red echelle se utiliza en el pico del blaze será

                                                                                                                            (5-36)

 La longitud de un orden en el plano focal del detector será

                                                                                                                  (5-37)

Donde el último factor es la separación angular de la red que está dada por:

                                                                       (5-38)

Siempre cosb se toma en el pico del blaze.

El rango espectral libre que es el intervalo entre dos longitudes de onda en órdenes sucesivos para el mismo ángulo de difracción será:

                                                                               (5-39)

 

Si queremos averiguar la separación entre órdenes se puede calcular dividiendo el rango espectral libre por la dispersión de la red cruzada D_cru .

                                                                                                                         (5-40)

 

 Existen muchos espectrógrafos echelle que van colgados del foco cassegrain y no son alimentados por fibra óptica . En CASLEO se encuentra uno de estos espectrógrafos , el cual se muestra de en la foto 5-3

  

Foto 5-3. Echelle cassegrain instalada en CASLEO.