3.1  ALGUNAS RELACIONES GENERALES DE LOS ESPECTRÓGRAFOS

 

En lo que sigue describiremos someramente algunas relaciones matemáticas útiles para utilizar espectrógrafos astronómicos pero también pueden resultar útiles para realizar diseños preliminares.

Si dos rayos colimados como los que muestra la Figura (5-5) tiene longitudes de onda l y l + d l dejan la red de difracción con ángulos que difieren en db  y entonces la separación sobre el plano focal de la cámara del espectrógrafo será:

 

dx =  F_cam db

donde F_cam es la distancia focal de la cámara, pero si

            

                                                             (5-2)

 

donde db/dl es la dispersión angular de la red o prisma.

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

Figura 5-5. Dispersión del espectro sobre el plano focal de la cámara del espectrógrafo

 

 

 

La ecuación fundamental de las redes de difracción (a ellas nos vamos a referir principalmente pues se usan casi con exclusividad en los espectrógrafos astronómicos modernos en lugar de prismas) es:                                     

 

  

                                                                               (5-3)

 

 

l    y a deben estar en las mismas unidades, m es el orden espectral, a es el espaciado entre los surcos o líneas de una red,  o sea es la inversa del número de líneas por milímetro de la red (n), a  es el ángulo de incidencia y b el de difracción. En la Figura (5-6) puede observarse claramente la nomenclatura utilizada para el caso de una red de reflexión. Los ángulos son positivos si están del mismo lado de la normal a la red que el rayo incidente, de lo contrario son negativos. 

 

Prestar atención al ángulo q que es el ángulo entre la normal a la red y la bisectriz del ángulo que forma la dirección incidente y la dirección difractada. Estas direcciones son fijas por construcción

 

                                                                      (5-4)

 

O también se puede expresar como se indica en la 5-5, utilizando las relaciones geométricas entre los ángulos de la Figura 5-6 y las relaciones trigonométricas para la suma y diferencia de dos ángulos.

Así tendremos,

                                                                           (5-5)

donde tuvimos en cuenta que el ángulo b es negativo por la convención adoptada anteriormente. Ahora podemos reemplazar el multiplicando del segundo miembro de 5-4 por las 5-5 y obtendremos,

                                          (5-6)

Utilizando los teoremas trigonométricos que nos indican que,

                                                        (5-7)

y

                                                        (5-8)

 

reemplazamos la 5-7 y la 5-8 en la expresión 5-6 y obtenemos,

                        (5-9)

Como el segundo y cuarto término de la sumatoria del segundo miembro de 5-9 se cancelan y el primero y el tercero son iguales obtenemos finalmente que,

                                                                          (5-10)

 

Reemplazando 5-10 en 5-4 donde también reemplazamos a por 10⁷/n obtenemos,

 

                           (5-11)

 

Obsérvese nuevamente  que el ángulo F es el que subtiende la dirección a la cámara y la dirección al colimador. Es decir que este ángulo es fijo por construcción en un espectrógrafo dado. En el espectrógrafo Boller&Chivens de CASLEO este ángulo vale 49°. Ver la Figura 5-6

 

Figura 5-6. Nomenclatura que se utilizará.

 

 

 

Las expresiones (5-3) y (5-4) nos dicen que la red de difracción nos produce un espectro para cada valor de m, y cuanto mayor es el m mayor es el ángulo de difracción b para una longitud de onda dada, o sea que tendremos una situación como la descripta por la Figura(5-7) para una red de transmisión, pero la situación es similar para una red de reflexión.

 

Regresemos a la expresión de la dispersión lineal 5-2. Ella nos dice que si queremos incrementar la dispersión es decir bajar algebraicamente el número dl/dx podemos para ello aumentar la distancia focal de la cámara o aumentar la dispersión angular de la red. A mediados del siglo pasado, se utilizaba la primer alternativa pues noera posible obtener comercialmente redes de gran dispersión angular. Analizaremos las consecuencias de esto más adelante. Con la placa fotográfica se usaba la dispersión lineal por mm para caracterizar un espectro o sea Å/mm. Hoy es más útil utilizar la resolución en Å/px o mejor dicho por elemento de resolución. Si el tamaño lineal del pixel es x entonces

 

  

 

                                                                                                                      (5-13)

 

 

 

 

A este te cociente se lo suele indicar con D y representa como dijimos la dispersión lineal.

La expresión para la dispersión D, puede expresarse también así:

                                                                                               (5-14)

 

y utilizando la ecuación dela red (5-11), podemos calcular la longitud de onda central que llamaremos l_c, que caerá sobre nuestro detector ubicado enun espectrógrafo dado.

 

                                                               (5-15)

despejando el producto mn tendremos,

 

                                                              (5-16)

 

y reemplazando 5-16 en 5-14obtendremos,

 

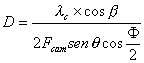                                                                        (5-17)

 

Si ahora utilizamos la expresión 5-5 para reemplazar el ángulob en la 5-17 y utilizamos la relación trigonométrica que indica que

 

obtendremos:

 

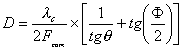                                                                                   (5-18)

 

Estas dos expresiones nos permiten calcular la inclinación que debo darle a la red de un espectrógrafo para obtener la longitud de onda que deseamos obtener sobre el detector. 

Por ejemplo supongamos que queremos trabajar en un espectrógrafo centrando nuestros espectros en 5000 A. El espectrógrafo tiene por construcción un ángulo F de 49°. Recordemos que este ángulo es el que forma el eje de la cámara y el eje del colimador y por lo tanto está fijo por construcción. Utilizando la 5-11 despejamos el senq y obtenemos la siguiente relación

Podemos construir la siguiente tabla para centrar 5000 A.

Tabla 5-1. Relación entre la inclinación de la red y el producto mn

mn      Senq         q

300     0,0824     4°,7

600     0,1648     9°,5

1200   0,3296   19°,2

2400   0,6593   41°,2

 

 Esta tabla nos dice simplemente que si queremos tener 5000 A sobre un espectrógrafo como elindicado podemos usar una red de 300 líneas por milímetro en primer orden(mn=300) o una red de 150 líneas por milímetro en segundo orden (mn=300) inclinándola 4°,7. La dispersión la calcularemos con la expresión 5-18. Para la situación planteada obtenemos que

 

                                                                           (5-19)

Si tomamos una cámaratípica de un espectrógrafo en el foco cassegrain con una distancia focal de140mm, la 5-19 se transforma en

 

Así podemos construir la siguiente tabla para nuestro ejemplo

Tabla 5-2. Dispersión paradistintos valores del producto mn.

mn         tgq         D [A/mm]

300   0,0826          224

600   0,1671          115

1200 0,3491            59

2400 0,8768            28

 

La Tabla 5-2 nos dice queen la situación descripta obtendremos el espectro centrado en 5000 A y con una dispersión de 59 A/mm su utilizamos una red de 1200 l/mm en primer orden o unade 600 líneas por milímetro en segundo orden

Para ver más sobre redes clickee aqui