4. LA TEMPERATURA VS. LA PROFUNDIDAD ÓPTICA
Como inicio de cualquier cálculo de un
modelo uno debe decidir que atmósfera particular se desea modelar.. Ello
implica seleccionar los parámetros: temperatura efectiva (
), gravedad
superficial (g) y composición
química. Como variable independiente en los cálculos de modelos suele usarse la
profundidad óptica ya definida.
Debemos determinar la relación entre T y t .
Queremos saber cual es el gradiente de temperatura que permite el flujo de radiación a través de la atmósfera. La opacidad se opondrá a dicho flujo. El coeficiente de absorción varía mucho con la frecuencia y por lo tanto la imposibilidad para la radiación de fluir libremente en determinafda frecuencia puede ser compensada en otra frecuencia donde el coeficiente de absorción sea menor.
Sabemos que el modelo de atmósfera deber+a cumplir con las condiciones de equilibrio que hemos visto. En particular la atmósfera deberá cumplir con la constancia del flujo total en cada capa. Esta condición es fundamental en la determinación de la distribución de la temperatura con la profundidad óptica que discutiremos.
En el caso gris y utilizando la aproximación de Eddington o Chandrashekar hemos podido resolver el problema de la distribución de temperatura analíticamente mientras que en el caso no gris debemos utilizar métodos numéricos para integrar las ecuaciones sobre las frecuencias. Se utiliza la constancia del flujo para el proceso de iteración. Se parte de una función fuente o distribución de temperatura aproximada que puede ser la proporcionada por Eddington por la relación 9.22 para el caso gris. Luego debemos calcular el flujo a través de la expresión 7.15 y verificar la constancia del flujo en cada capa. Como seguramente no lo será debemos corregir la función fuente o distribución inicial de la temperatura (recordemos que estamos bajo la suposición de LTE) para volver a recalcular el flujo hasta obtener la satisfacción de la constancia del mismo. Normalmente la constancia del flujo se especifica a valores entre 0.1 y 1%.
Métodos para realizar la tarea iterativa descripta pueden encontrarse en Avrett and Krook (1963). Otros métodos pueden encontrarse en Kalkofen (1987).
A continuación describimos un método iterativo como ejemplo sobre la forma de resolver el problema planteado.
4.1 El procedimiento de Unsold-Lucy
Partimos de la aproximación de Eddington donde
(11.4)
integraremos esa igualdad sobre las frecuencias,
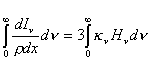(11.5)
de manera que se mantiene la igualdad,
(11.6)
donde hemos utilizado la definición de la opacidad media pesada por el flujo (9.172)
(11.7)
Hagamos uso ahora del coeficiente de absorción media de Planck definido en 9.178 y su opacidad óptica correspondiente
, (11.8)
de ese modo
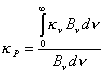(11.9)
Luego tendremos,
(11.10)
y
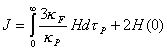(11.11)
donde hemos utilizado la condición isotrópica para la condición de borde en la superficie,
Utilizando ahora la ecuación de continuidad,
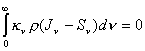(11.12)
conjuntamente
con la suposición de ETL, 
entonces tendremos
que,
(11.13)
Si
multiplicamos por 
e integramos sobre
las frecuencias tendremos,
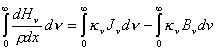(11.14)
(11.15)
siendo kJ la opacidad media definida en 9.181
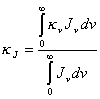(11.16)
y si
dividimos ahora por 
tendremos,
(11.17)
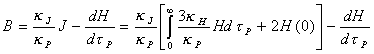(11.18)
donde hemos hecho uso de la ecuación (11.11)
Suponganos ahora una solución aproximada B´(t) , la cual predice un flujo H´ que varía con la profundidad óptica. Pero la solución verdadera B(t), dará un flujo constante H.
Si escribimos ahora
y
y donde 
será el error en el
flujo y 
será la corrección
requerida por la función fuente. Por lo tanto sustrayendo la 11.18 resuelta
para B de la 11.18 resuelta para B’ tendremos,
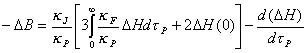(11.19)
Si estimamos una T(t) ello nos permitirá
calcular Sn = B(T) y de 
uno puede obtener 
.
De la ecuación 7.40
obtendremos Jn(t) utilizando Sn
y
entonces calcularemos 
y a través de la
ecuación (11.11) obtendremos H’(t) y también
y 
.
Si ahora sustituimos en (11.19) podemos calcular la corrección a nuestra suposición inicial para la función fuente. Así continuamos hasta obtener la convergencia del procedimiento.
4.2
LA DISTRIBUCIÓN DE TEMPERATURA SOLAR
Para saber sobre la distribución de temperatura en el Sol, necesitamos un experimento que dependa de lo que ocurre en las distintas capas del Sol. Esa observación es el oscurecimiento al limbo. La distribución de temperatura en el Sol puede obtenerse de las observaciones de dicho efecto. Sabemos por lo explicado en el caso gris que el oscurecimiento al limbo tiene lugar porque al decrecer la función fuente hacia afuera en una estrella como el Sol , cuando miramos hacia el limbo estamos viendo radiación cada vez más superficial y que por lo tanto emiten menos cantidad de energía. Sabemos cual es la intensidad de la radiación en la superficie que está descripta por 9. 34. En el caso gris la función fuente es una función lineal con la profundidad óptica, tal como encontramos en la 9.15. Si reemplazamos esta última en la 9.34 obtenemos como resultado la 9.38
Quiere decir entonces que para cos theta = tau la intensidad específica monocromática en la superficie será igual a la función fuente para la profundidad óptica tau. Esta relación que nos permite obtener información sobre la distribución de temperatura en las capas más profundas del Sol se conoce como relación Eddington - Barbier.
Para obtener la distribución de temperatura en el Sol debemos hacer observaciones del oscurecimiento al limbo, generalmente se obtiene el cociente entre la intensidad en el punto observado y la intensidad en el centro del disco solar.
Se obtiene así 
Observando la forma del coeficiente al limbo estamos determinando la forma de la función fuente. Luego obteniendo a través de otro conjunto de observaciones
se obtiene la función fuente en valor absoluto. Como suponemos LTE igualamos la función fuente con la ley de Planck y así derivamos la temperatura para la capa del Sol correspondiente. Estas observaciones pueden combinarse con observaciones de la variación del oscurecimiento al limbo con la longitud de onda. Por lo tanto lo ideal es tener observaciones del oscurecimiento al limbo para un amplio rango de longitudes de onda.
Varios grupos de investigadores realizaron este tipo de observaciones para determinar la distribución de la temperatura solar. Entre ellos se encuentran
Elste (1967)
Holweger and Muller
(1974)
entre otros.
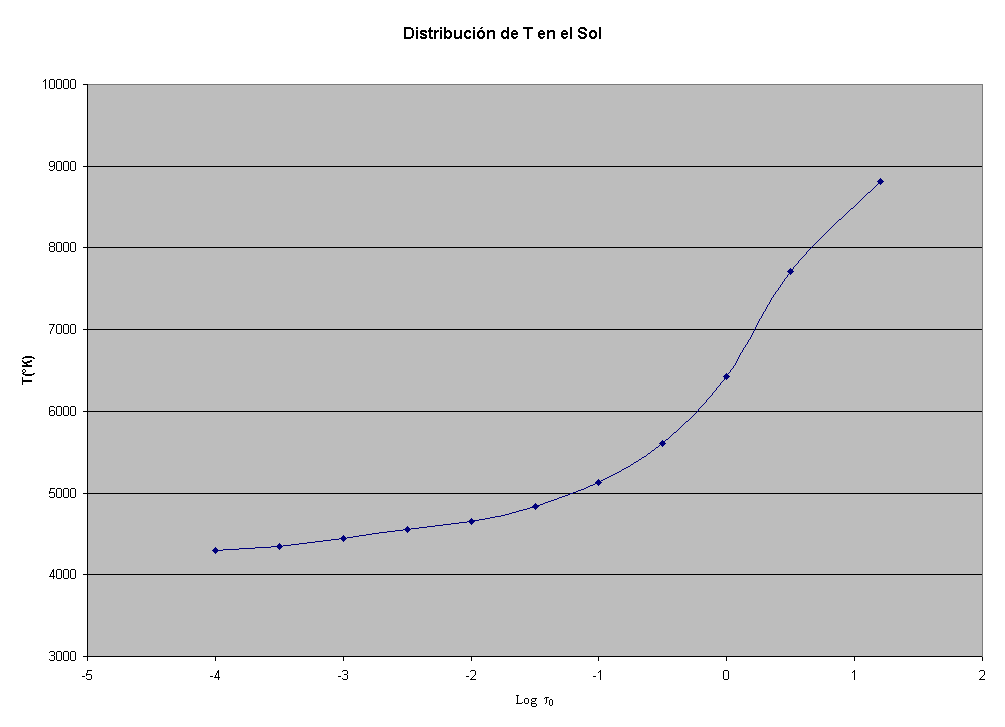
La Figura 11.2 muestra un promedio de la distribución de temperatura solar de los diferentes trabajos en función de la profundidad óptica a 5000 A. Las discrepancias comienzan a hacerse notables para valores del log t0 menores que -4 y mayores que 0.5 es decir que, para profundidades ópticas entre 0.0001 y 3 los resultados son muy aceptables. La mayor parte del continuo y la mayoría de las líneas en las estrellas normales se forman en esas profundidades.
La distribución de temperatura en el Sol para una profundidad óptica de referencia se encuentra en la Tabla 11.1 publicada por Gray (1992)
Tabla 11.1. Distribución de Temperatura en el Sol. Promedios de varias mediciones por diferentes autores.
| t0 | T(°K) |
| 0.0001 | 4300 |
| 0.0003 | 4350 |
| 0.001 | 4450 |
| 0.003 | 4550 |
| 0.01 | 4650 |
| 0.025 | 4800 |
| 0.04 | 4874 |
| 0.06 | 4995 |
| 0.1 | 5132 |
| 0.16 | 5294 |
| 0.25 | 5490 |
| 0.40 | 5733 |
| 0.63 | 6043 |
| 1.00 | 6429 |
| 1.58 | 6904 |
| 2.51 | 7467 |
| 3.98 | 7962 |
| 6.30 | 8358 |
| 10.0 | 8630 |
| 15.8 | 8811 |
Nos preguntamos ahora si será posible utilizar un procedimiento similar para las otras estrellas. Sabemos que no existen observaciones en gran escala del oscurecimiento al limbo en otras estrellas. El método de requerir la constancia del flujo ya expuesto es relativamente simple de aplicar cuando no se tienen en cuenta las líneas espectrales pero evidentemente la introducción del efecto de las líneas aumenta la complejidad de los cálculos. Es necesario incluir muchos más puntos de longitud de onda para efectuar las integraciones cuando incluimos la opacidad de las líneas. El efecto general de incluir la opacidad de las líneas es aumentar la temperatura de las capas más profundas y disminuir la temperatura de las capas más superficiales. Hoy todos los cáculos de modelos incluyen la opacidad debida a las líneas porque las computadoras poderosas están al alcance de casi todos los investigadores en el tema. El otro problema del método de la constancia de flujo es el error que introduce el tratamiento de la convección con su parámetro libre, longitud de mezcla, aunque es escaso el flujo que proviene de las capas donde se produce la convección por lo menos en las estrellas tempranas.
Un procedimiento aproximado, para estrellas del tipo solar por lo menos, es tratar de ajustar la distribución de temperatura solar que hemos descripto a la nueva estrella a través de algún procedimiento adecuado. El caso gris nos puede mostrar algún indicio.
Si recordamos la distribución de temperatura encontrada para el caso gris en la solución de Eddington (9.22),
(11.20)
y expresamos esta relación para el Sol tendremos,
(11.21)
luego dividiendo miembro a miembro (11.20) y (11.21) tendremos,
(11.22)
La comparación de la distribución de temperatura encontrada para las mismas estrellas por el método de la distribución solar ajustada y por el método completamente teórico de la constancia del flujo, indica que es posible utilizar la temperatura solar ajustada para objetos de hasta dos veces la temperatura efectiva del Sol es decir unos 11.000 °K aproximadamente. De todos modos el método de la temperatura solar ajustada puede ser utilizado para interpolar en las grillas de modelos a los efectos de ajustar la distribución de temperatura en alguna estrella que sea de nuestro interés.