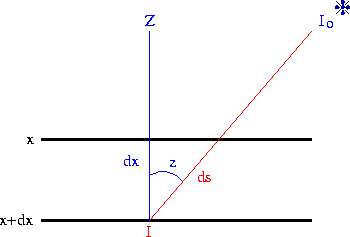
As ondas eletromagnéticas, desde os raios ![]() , passando
pelos raios-X, luz visível, infra-vermelho, micro-ondas e
ondas de rádio, viajam à velocidade da luz
, passando
pelos raios-X, luz visível, infra-vermelho, micro-ondas e
ondas de rádio, viajam à velocidade da luz
![]() m/s,
e são caracterizadas por um comprimento de onda
m/s,
e são caracterizadas por um comprimento de onda ![]() ,
que mede a distância entre dois picos
(máximos de campo elétrico ou magnético)
sucessivos,
e uma frequência,
,
que mede a distância entre dois picos
(máximos de campo elétrico ou magnético)
sucessivos,
e uma frequência, ![]() ,
que é o número de picos
que passam por um ponto em uma unidade de tempo. A relação entre
estas propriedades pode ser expressa como:
,
que é o número de picos
que passam por um ponto em uma unidade de tempo. A relação entre
estas propriedades pode ser expressa como:
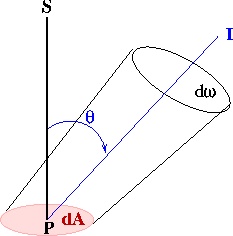
A grandeza mais característica de um campo de radiação
é uma constante chamada intensidade específica monocromática
![]() , que é a
energia por unidade de área e por unidade de tempo que está
sendo emitida pela fonte, em um
intervalo de frequências
, que é a
energia por unidade de área e por unidade de tempo que está
sendo emitida pela fonte, em um
intervalo de frequências ![]() .
Na posição do observador, essa energia
é captada ao longo de uma direção
.
Na posição do observador, essa energia
é captada ao longo de uma direção ![]() , que é o ângulo
entre a linha de visada e a direção normal à superfície
emissora, e dentro de um ângulo sólido
, que é o ângulo
entre a linha de visada e a direção normal à superfície
emissora, e dentro de um ângulo sólido ![]() , que será tanto
menor quanto mais distante estiver o objeto. Formalmente, a
intensidade específica é definida como a energia que atravessa
um elemento de área
, que será tanto
menor quanto mais distante estiver o objeto. Formalmente, a
intensidade específica é definida como a energia que atravessa
um elemento de área ![]() , por intervalo de tempo, dentro de um
elemento de ângulo sólido
, por intervalo de tempo, dentro de um
elemento de ângulo sólido ![]() , na direção
, na direção ![]() ,
dentro de um intervalo de frequências
,
dentro de um intervalo de frequências ![]() e
e
![]() ,
ou seja:
,
ou seja:
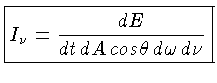
A intensidade específica, por sua definição, não depende
da distância da fonte emissora. Geralmente é medida em
![]() . Um
. Um ![]() , chamado de esferorradiano,
é uma unidade de ângulo sólido.
, chamado de esferorradiano,
é uma unidade de ângulo sólido.
Podemos também definir a intensidade específica monocromática por intervalo de comprimento de onda, lembrando que, por definição:
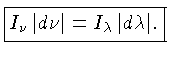
A intensidade específica integrada em todo o espectro de frequências é dada por:
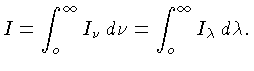
Outra quantidade de grande interesse é o fluxo F, que é a energia por unidade de área e por unidade de tempo que chega ao detector, e é o que se mede realmente. Formalmente, o fluxo em uma certa frequência, em um dado ponto e em um dada direção e sentido, é a quantidade líquida de energia radiante cruzando a unidade de área, por unidade de tempo, e por intervalo de frequência, ou seja,
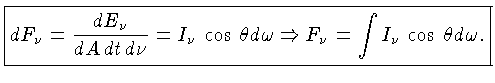
O fluxo portanto significa potência através de uma superfície,
e é expresso em
![]() , ou em
, ou em
![]() .
.
O fluxo integrado no espectro de frequências será:
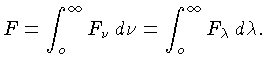
Ao contrário da intensidade específica, o fluxo de radiação
cai com o quadrado da distância (![]() ), de forma que o fluxo que chega no
detector é muito menor do que o fluxo na superfície da fonte, estando
diluído por um fator de
), de forma que o fluxo que chega no
detector é muito menor do que o fluxo na superfície da fonte, estando
diluído por um fator de
![]() .
.
Para uma fonte esférica de raio R não colimada, o fluxo na sua superfície será
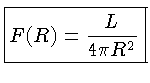
O fluxo a uma distância ![]() da fonte será
da fonte será
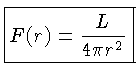
Nesse caso, ![]() é o fluxo integrado sobre toda a
superfície da fonte, e a luminosidade
é o fluxo integrado sobre toda a
superfície da fonte, e a luminosidade ![]() pode ser
obtida diretamente multiplicando o fluxo dela proveniente pela
área sobre a qual o fluxo se distribui, integrado sobre todas
as frequências.
pode ser
obtida diretamente multiplicando o fluxo dela proveniente pela
área sobre a qual o fluxo se distribui, integrado sobre todas
as frequências.
Em 1856, Norman Robert Pogson (1829-1891) verificou
que a percepção de brilho do olho
humano é logarítmico. O olho humano é capaz de detectar
variações de intensidade sobre aproximadamente 10 ordens
de magnitude, isto é, de valores que vão de 1 a ![]() .
.
As intensidades realmente medidas dependem
da sensibilidade espectral do equipamento
(fonte + detector).
Se chamamos de
![]() a eficiência espectral
do equipamento, normalizada, temos:
a eficiência espectral
do equipamento, normalizada, temos:
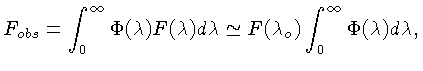
O corpo humano através do qual a radiação atravessa,
afeta as medidas.
Seu efeito
é absorver e espalhar a radiação em outras
direções, processos esses que são descritos por um coeficiente
de absorção ![]() , usualmente medido em
, usualmente medido em ![]() . A perda relativa de
fluxo sofrida pela luz ao atravessar uma distância
. A perda relativa de
fluxo sofrida pela luz ao atravessar uma distância ![]() ao longo da
camada será:
ao longo da
camada será:
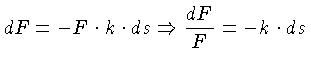
Chamando ![]() o fluxo da fonte, o fluxo que chega o
detector, obtido por integração da equação acima,
como veremos abaixo é:
o fluxo da fonte, o fluxo que chega o
detector, obtido por integração da equação acima,
como veremos abaixo é:
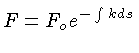
Chamando
![]() = profundidade ótica,
= profundidade ótica,