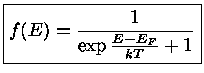
Qualquer sistema a uma temperatura absoluta de zero graus Kelvin encontra-se no estado fundamental. Se o sistema for de férmions, isto é, partículas com spin semi-inteiro, todos os estados abaixo do potencial de Fermi Ef estarão ocupados. Estatisticamente, todos os estados com energia E abaixo do potencial de Fermi estarão ocupados, com probabilidade f(E)=1, e todos acima estarão vazios, com probabilidade f(E)=0. Pressionando OK, o applet ilustra a situação para T=0. Se a temperatura não é zero, a probabilidade de um estado de energia E estar ocupado segue a distribuição de Fermi-Dirac:
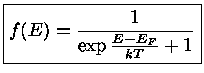
onde k é a constante de Boltzmann. Pressionando Increase o applet demonstra a evolução dinâmica de f(E) com o aumento da temperatura.
Volta: Temperatura Anterior: Interiores Estelares
![]()