As estrelas são consideradas binárias
próximas quando ocorre transferência
de massa em alguma fase de sua evolução.
Se definirmos 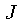 como o momentum angular total em
relação ao centro de massa:
como o momentum angular total em
relação ao centro de massa:
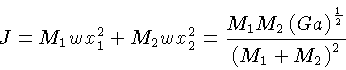 |
(1) |
Resolvendo para 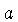 :
:
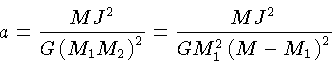 |
(2) |
logo,
se a massa total e o momentum angular forem conservados durante
a transferência de massa,
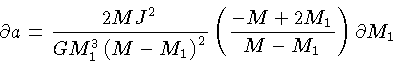 |
(3) |
com
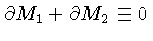 .
Esta equação nos dá a relação entre a massa transferida e a
mudança na separação entre as estrelas.
.
Esta equação nos dá a relação entre a massa transferida e a
mudança na separação entre as estrelas.
Para uma estimativa da ordem de grandeza, podemos expressar
o raio da esfera com o mesmo volume que o lóbulo
de Roche da componente 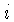 como:
como:
Existem quatro maneiras de preencher o lóbulo de Roche:
- crescimento de uma das componentes por evolução.
- redução da separação entre as componentes
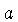 por emissão de vento magnético ou ondas gravitacionais.
por emissão de vento magnético ou ondas gravitacionais.
- aumento de raio da receptora de massa
por rejeição do material acretado ou
ignição termonuclear na base da camada acretada.
- colisão da binária com outra estrela de
um aglomerado denso que reduza a separação
entre as componentes.
Quando a transferência de massa se inicia:
- se a doadora não tinha envelope convectivo,
o lóbulo de Roche continua cheio e portanto
continua a transferência de massa até que
a razão das massas se inverta:
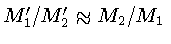 .
.
- se a doadora já possuia envelope convectivo, ela continua
perdendo massa até que a massa do envelope de hidrogênio
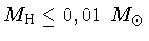 , como nas estrelas
sdO e sdB.
, como nas estrelas
sdO e sdB.
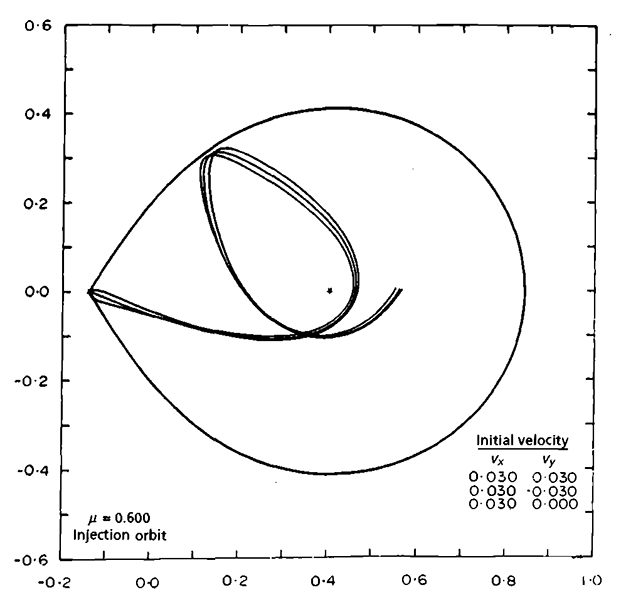
Órbita da matéria que passa pelo L1, de acordo com os cálculos de
Brian P. Flannery 1975, Astrophysical Journal, 201, 661.



Próxima: Envelope Comum
Volta: Interiores Estelares
 Astronomia
e Astrofísica
Astronomia
e Astrofísica

©
Modificada em 29 out 2014
![]() como o momentum angular total em
relação ao centro de massa:
como o momentum angular total em
relação ao centro de massa:
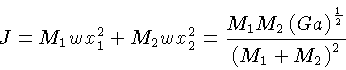
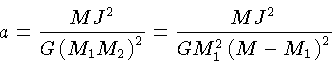
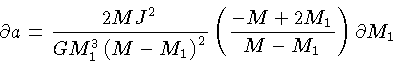
![]() como:
como:
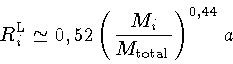

![]()