- Deduza a relação entre a energia do gás
e a temperatura, para um gás não degenerado,
isto é, um gás que pode ser representado pela
distribuição de Maxwell-Boltzmann
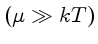 .
.
- a) para um gás não-relativístico. b) para
um gás relativístico,
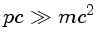 , onde
a energia da partícula é dada por
, onde
a energia da partícula é dada por
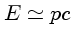 .
.
- A constante de normalização
para um gás relativístico e não relativístico
é a mesma?
- Derive a relação geral entre pressão de um gás ideal e
a distribuição de velocidade do gás. Derive a relação
entre a pressão e a densidade para um gás completamente
degenerado e ultra-relativístico.
- Derive a equação de equilíbrio hidrostático.
- Quanto tempo leva para um desvio de 1% no equilíbrio provocar
uma variação de 50% no raio?
- Avalie a
temperatura no interior do Sol e de uma estrela tipo 0 (
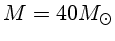 ,
,
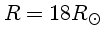 ).
).
- Usando a temperatura
obtida no ítem anterior, calcule a razão entre a pressão do gás
e a pressão de
radiação no interior destes dois modelos, sabendo que
a densidade central do modelo de
1
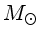 é
é
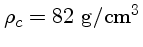 , enquanto
que para 40
, enquanto
que para 40 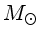 a densidade central é
a densidade central é
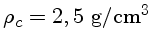 .
.
- Qual o valor do peso molecular médio
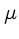 para uma estrela na seqüência principal?
para uma estrela na seqüência principal?
- Demonstre o teorema de virial
para um gás ideal e explique o que ele significa.
Se o raio da estrela aumenta por uma fator de dois, quando ela
sai da sequência principal, de quanto varia a temperatura?
E para
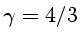 ?
?
- A partir da lei do gás adiabático, derive a condição
de equilíbrio radiativo de Schwarzschild.
- Derive a condição de equilíbrio térmico para o caso geral
de produção de energia nuclear, contração e emissão de
neutrinos.
- Qual é o valor de q=(1-Mr/M)
que corresponde ao centro e qual
corresponde à fotosfera?
Como a zona de convecção exterior do Sol se extende até
q=0,0035, qual é a fração do raio correspondente?
E qpp (equação 7 de Abundâncias Químicas, para o ciclo pp)?
- Localize no código fonte do programa
ZAMS
as 4 equações de equilíbrio
das estrelas e demonstre que as equações do programa são as
mesmas que deduzimos.
- Localize no código fonte do MESA
as 4 equações de equilíbrio
das estrelas e demonstre que as equações do programa são as
mesmas que deduzimos.
- Derive
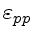 e
e
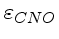 para os modelos calculados pelo ZAMS, e também
para
para os modelos calculados pelo ZAMS, e também
para
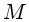 |
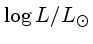 |
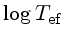 |
R |
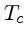 |
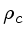 |
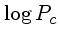 |
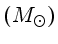 |
|
(K) |
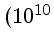 cm) cm) |
(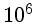 K) K) |
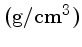 |
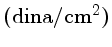 |
| 1,75 |
1,031 |
3,948 |
9,683 |
20,22 |
66,5 |
17,25 |
| 1,5 |
0,759 |
3,892 |
9,141 |
19,05 |
76,7 |
17,28 |
- Utilize a definição de
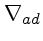 calcular seu valor para um gás ideal. Compare
com os valores calculados pelo programa ZAMS e diga por que
não é o mesmo para todas as massas.
calcular seu valor para um gás ideal. Compare
com os valores calculados pelo programa ZAMS e diga por que
não é o mesmo para todas as massas.
- Qual é o valor de
 na fotosfera, para as diferentes
massas?
na fotosfera, para as diferentes
massas?
- Derive a opacidade por espalhamento de elétrons. Calcule
a opacidade média de Rosseland para esta fonte de opacidade.
- Derive a relação entre a taxa de geração de
energia por unidade de massa e a secção de choque de uma
reação nuclear. Calcule a energia em que a reação nuclear
entre duas partículas é máxima.
Evolução Estelar
 Astronomia e Astrofísica
Astronomia e Astrofísica

©
Modificada em 30 ago 2011
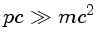 , onde
a energia da partícula é dada por
, onde
a energia da partícula é dada por
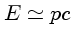 .
.
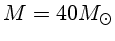 ,
,
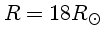 ).
).
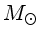 é
é
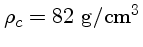 , enquanto
que para 40
, enquanto
que para 40 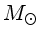 a densidade central é
a densidade central é
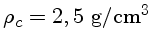 .
.
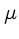 para uma estrela na seqüência principal?
para uma estrela na seqüência principal?