Na nossa derivação de transporte de energia por convecção,
supusemos que o elemento convectivo se desloca com uma velocidade ![]() por uma distância
por uma distância ![]() e então se dissolve no meio, liberando
o calor. No topo da zona de convecção, onde o gradiente de
temperatura real se torna menor do que o gradiente de temperatura
adiabático, todos os elementos convectivos supostamente param,
não penetrando nas camadas superiores, que são estáveis.
Essa hipótese não é real, pois alguns elementos do fluido
excederão a borda, entrando na região estável.
Os efeitos desse sobreimpulso (overshooting) são: misturar a matéria
de composição química diferente depois da interface
convectiva e transportar algum calor, ou seja, uma maior mistura (extra-mixing).
No modelo de comprimento de mistura, o transporte
de fluxo pela energia cinética dos
elementos não é incluída.
Na zona de convecção
no núcleo de estrelas
massivas, o overshooting afeta o tempo de vida, pois mistura
combustível nuclear e pode levar restos de queima nuclear
até a superfície das estrelas, onde se tornam visíveis,
como no caso das estrelas Wolf-Rayet. O grande problema é
estimar a desaceleração do elemento e, portanto, quantificar
o overshooting.
Bernd Freytag,
Hans Günther-Ludwig e
Matthias Steffen
(1996, A&A, 313, 497) estudaram o overshooting
nas camadas superficiais do Sol,
estrelas A e anãs brancas DAs através de modelos hidrodinâmicos.
Nas suas simulações numéricas, os movimentos convectivos se extendem
bem além das zonas instáveis. Para uma estrela tipo A de sequência
principal, a massa na zona de "overshooting" é maior do que
a massa na zona de convecção por um fator de 10. Para uma anã
branca DA com Tef=12 200 K, a massa na
zona de "overshooting" é maior do que
a massa na zona de convecção por um fator de 100!
Isto ocorre porque,
nas simulações, o material descendente se
concentra em tubos estreitos com altas velocidades, cercados de
largas regiões ascendentes com velocidades comparativamente baixas.
e então se dissolve no meio, liberando
o calor. No topo da zona de convecção, onde o gradiente de
temperatura real se torna menor do que o gradiente de temperatura
adiabático, todos os elementos convectivos supostamente param,
não penetrando nas camadas superiores, que são estáveis.
Essa hipótese não é real, pois alguns elementos do fluido
excederão a borda, entrando na região estável.
Os efeitos desse sobreimpulso (overshooting) são: misturar a matéria
de composição química diferente depois da interface
convectiva e transportar algum calor, ou seja, uma maior mistura (extra-mixing).
No modelo de comprimento de mistura, o transporte
de fluxo pela energia cinética dos
elementos não é incluída.
Na zona de convecção
no núcleo de estrelas
massivas, o overshooting afeta o tempo de vida, pois mistura
combustível nuclear e pode levar restos de queima nuclear
até a superfície das estrelas, onde se tornam visíveis,
como no caso das estrelas Wolf-Rayet. O grande problema é
estimar a desaceleração do elemento e, portanto, quantificar
o overshooting.
Bernd Freytag,
Hans Günther-Ludwig e
Matthias Steffen
(1996, A&A, 313, 497) estudaram o overshooting
nas camadas superficiais do Sol,
estrelas A e anãs brancas DAs através de modelos hidrodinâmicos.
Nas suas simulações numéricas, os movimentos convectivos se extendem
bem além das zonas instáveis. Para uma estrela tipo A de sequência
principal, a massa na zona de "overshooting" é maior do que
a massa na zona de convecção por um fator de 10. Para uma anã
branca DA com Tef=12 200 K, a massa na
zona de "overshooting" é maior do que
a massa na zona de convecção por um fator de 100!
Isto ocorre porque,
nas simulações, o material descendente se
concentra em tubos estreitos com altas velocidades, cercados de
largas regiões ascendentes com velocidades comparativamente baixas.
Vittorio M. Canuto, em seu artigo de 2000 Semiconvection and Overshooting: Schwarzschild and Ledoux Criteria Revisited, no Astrophysical Journal, 534, L113, discute que o critério de Schwarzschild requer overshooting enquanto o critério de Ledoux não necessariamente. No seu artigo Overshooting in Stars: a New Formulation [Stellar Structure: Theory and Test of Connective Energy Transport, ASP Conference Series, Vol. 173. Edited by Alvaro Gimenez, Edward F. Guinan, and Benjamin Montesinos. Astronomical Society of the Pacific (San Francisco), ISBN: 1-886733-95-3 (1999), p.133] ele deduz um modelo para calcular o overshooting.
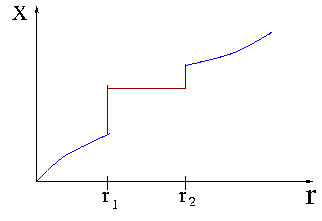
Semi-convecção é a mistura de elementos na interface
da zona de convecção, devido à existência de descontinuidades
na composição química. Por exemplo, para uma estrela
de 10 ![]() , a zona de convecção se expande com o tempo,
causando uma descontinuidade na abundância do hidrogênio, X.
Como a opacidade é dominada por espalhamento de elétrons
e, como veremos na secção (T10),
, a zona de convecção se expande com o tempo,
causando uma descontinuidade na abundância do hidrogênio, X.
Como a opacidade é dominada por espalhamento de elétrons
e, como veremos na secção (T10),
![]() é descontínuo e, portanto,
é descontínuo e, portanto,
![]() também, pois a equação de equilíbrio
radiativo (equação 1.51) nos dá:
também, pois a equação de equilíbrio
radiativo (equação 1.51) nos dá:
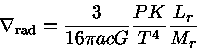 |
(1) |
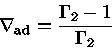 |
(2) |
 Outro efeito que precisa ser levado em conta é a mistura por
dedos de sal (salt fingers), também chamado de mistura termoalina,
causados por instabilidade de difusão dupla,
em que camadas de diferentes densidades e temperaturas se misturam,
como as calculadas por Matteo Cantiello e Evert Glebbeek para
as gigantes vermelhas. O nome vem do fenômeno nos oceanos, quando
água mais quente e salgada está sobre uma camada de água menos
salgada e mais fria.
Outro efeito que precisa ser levado em conta é a mistura por
dedos de sal (salt fingers), também chamado de mistura termoalina,
causados por instabilidade de difusão dupla,
em que camadas de diferentes densidades e temperaturas se misturam,
como as calculadas por Matteo Cantiello e Evert Glebbeek para
as gigantes vermelhas. O nome vem do fenômeno nos oceanos, quando
água mais quente e salgada está sobre uma camada de água menos
salgada e mais fria.
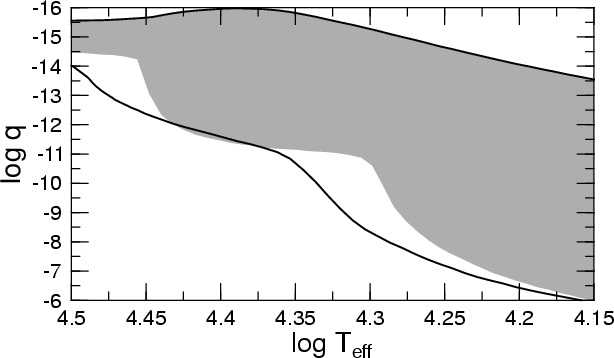
Uma das razões da necessidade de nova teoria vem do fato de que no Sol, os modelos, por exemplo, L. Deng & D.R. Xiong (2008, IAU Symposium 252, ed. L. Deng, & K. L. Chan, Cambridge University Press, p. 83) e simulações numéricas de overshooting resultam em uma região uma ordem de magnitude maior do que a resultante da inversão dos dados de hélio-sismologia, por exemplo, Jorgen Christensen-Dalsgaard et al. 2011, Monthly Notices of the Royal Astronomical Society, 414, 1158.
Q. S. Zhang, em seu artigo de 2013, no Astrophysical Journal Supplement (arXiv:1303.0139), discute que o overshooting pode ser representado por difusão, com um coeficiente único para o Sol e para estrelas entre 2 e 10 massas solares. Em geral um único coeficiente não consegue representar condições muito distintas.
Dada a massa e a idade de uma estrela, sua estrutura interna completa é determinada por somente uma outra propriedade básica, sua composição química inicial.
Normalmente, a composição é especificada por três parâmetros: X, Y, Z.
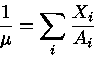
Como um exemplo, um gás de carbono puro tem ![]() ,
ou seja
,
ou seja ![]() , enquanto um gás de hidrogênio puro tem
, enquanto um gás de hidrogênio puro tem
![]() , ou seja
, ou seja ![]() .
.
Se uma fração ![]() do elemento
do elemento ![]() , com
, com ![]() prótons, está ionizada,
o peso molecular médio dos elétrons,
prótons, está ionizada,
o peso molecular médio dos elétrons, ![]() será:
será:
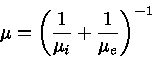
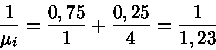
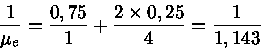
Em 2005, o mesmo Nicolas Grevesse, com Martin Asplund & A. Jacques Sauval publicaram redeterminações da composição solar, European Astronomical Society Publications Series, Volume 17, 2005, p.21, usando novas probabilidades de transição, modelos tridimensionais e fora de equilíbrio termodinâmico local, e encontraram Y=0,165, o que levou a modelos completamente diferentes e inconsistentes com as observações heliosismológicas (Sarbani Basu & H. M. Antia, no artigo Helioseismology and solar abundances, 2008 Physics Reports, 457, 217). Aldo M. Serenelli e Sarbani Basu, no Astrophysical Journal de 2010 (719, 865), utilizam a abundância superficial do Sol obtida pela sismologia, de YsuperficialSol=0,2485 ± 0,0035, com uma incerteza na taxa de difusão de 20%, e os modelos de convecção, para encontrar a abundância primordial de YinicialSol=0,278 ± 0,006.
A idade do Sol, obtida pelo decaimento radiativo em meteoritos antigos, desde o início da sequência principal, está entre 4,563 e 4,576 bilhões de anos, de acordo com Gerald J. Wasserburg em John N. Bahcall & Marc Pinsonneault (1995, Reviews of Modern Physics, 67, 781).
A mais recente determinação das abundâncias solares é Nicolas Grevesse, Martin Asplund, A. Jacques Sauval & Pat Scott, 2010, Astrophysics & Space Science, 328, 179, obtendo X=0,7380, Y=0,2485 e Z=0,0134, consistente com a heliosismologia.
Nas regiões radiativas, não há troca de matéria
entre as camadas da estrela se desprezarmos a difusão.
Portanto, as frações dos elementos químicos
![]() só podem mudar se as reações nucleares criarem
ou destruírem os elementos de tipo
só podem mudar se as reações nucleares criarem
ou destruírem os elementos de tipo ![]() , no elemento
de massa em consideração.
, no elemento
de massa em consideração.
A freqüência das reações nucleares
é descrita por taxas de reação ![]() ,
representando o número de reações por unidade de volume
e tempo que transformam elementos do tipo
,
representando o número de reações por unidade de volume
e tempo que transformam elementos do tipo ![]() em elementos
do tipo
em elementos
do tipo ![]() . Em geral, um elemento do tipo
. Em geral, um elemento do tipo ![]() pode
ser afetado simultaneamente por muitas reações,
algumas que criam o elemento
pode
ser afetado simultaneamente por muitas reações,
algumas que criam o elemento
![]() ,
e outras que o destroem
,
e outras que o destroem
![]() .
Essas taxas de reações nos dão diretamente
a variação de
.
Essas taxas de reações nos dão diretamente
a variação de ![]() por segundo.
Como
por segundo.
Como
A reação
![]() em que um elemento do tipo
em que um elemento do tipo ![]() é transformado em um elemento do tipo
é transformado em um elemento do tipo ![]() está associada
a uma liberação de energia
está associada
a uma liberação de energia
![]() . Na equação de conservação de energia, nós
usamos a taxa de geração de energia por unidade de massa
. Na equação de conservação de energia, nós
usamos a taxa de geração de energia por unidade de massa
![]() , que normalmente contém contribuições
de muitas reações diferentes:
, que normalmente contém contribuições
de muitas reações diferentes:
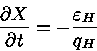
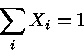
 Efeitos microscópicos (movimentos randômicos)
também podem mudar a composição
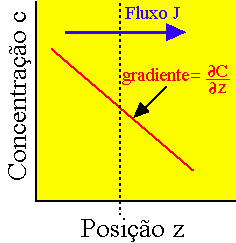
química de uma camada no interior da estrela. Se existem
gradientes nas abundâncias dos elementos, a difusão tende
a reduzir as diferenças. A difusão se dá por movimentos
randômicos das partículas. A teoria macroscópica da
difusão foi proposta em 1855 pelo
fisiologista alemão Adolf Eugen Fick (1829-1901)
[Ann. Physik Leipzig, 170, p 59, 1855],
que mais tarde inventaria as lentes de contato,
propondo duas
leis, relacionado o fluxo de partículas
Efeitos microscópicos (movimentos randômicos)
também podem mudar a composição
química de uma camada no interior da estrela. Se existem
gradientes nas abundâncias dos elementos, a difusão tende
a reduzir as diferenças. A difusão se dá por movimentos
randômicos das partículas. A teoria macroscópica da
difusão foi proposta em 1855 pelo
fisiologista alemão Adolf Eugen Fick (1829-1901)
[Ann. Physik Leipzig, 170, p 59, 1855],
que mais tarde inventaria as lentes de contato,
propondo duas
leis, relacionado o fluxo de partículas ![]() com
o gradiente da concentração
com
o gradiente da concentração
![]() por um coeficiente de difusão
por um coeficiente de difusão ![]() ,
em analogia ao transporte de calor por um gradiente de temperatura:
,
em analogia ao transporte de calor por um gradiente de temperatura:
| (9) |
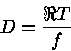
Escrevendo o fluxo
![]() , onde
, onde ![]() é a velocidade
de difusão, obtemos
é a velocidade
de difusão, obtemos
| (11) |
Uma generalização da velocidade de difusão
(equação 10)
é:
Vamos, primeiro, considerar o efeito de difusão por concentração e por temperatura.
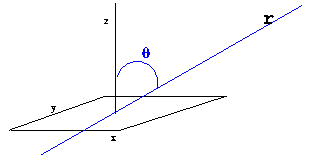
Se expandirmos ![]() e
e ![]() em
em ![]() na equação
(14),
e em uma equação correspondente para o fluxo
na equação
(14),
e em uma equação correspondente para o fluxo ![]() na direção
na direção
![]() :
:
![J^\pm = \frac{1}{6}[c(0)\mp\frac{\partial c}{\partial z... ...ft[\bar{v}(0)\mp\frac{\partial \bar{v}}{\partial z}\ell]](img77.gif) |
(15) |
Consideremos a velocidade de difusão relativa
![]() devido ao movimento de dois tipos diferentes de partículas
(1,2), com fluxos
devido ao movimento de dois tipos diferentes de partículas
(1,2), com fluxos ![]() e
e ![]() , e concentrações
, e concentrações ![]() e
e ![]() :
:
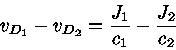 |
(17) |
| (18) |
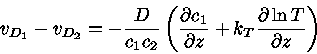 |
(19) |
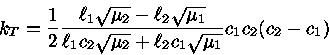 |
(21) |
Da equação (20)
podemos ver que o coeficiente
de difusão é da ordem de
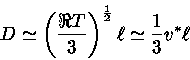 |
(22) |
Se considerarmos uma mistura de hidrogênio e hélio,
![]() é a velocidade de difusão.
Se
é a velocidade de difusão.
Se ![]() , o hidrogênio se difunde na direção
de menor temperatura, isto é, para cima na estrela.
Para a região central do Sol (
, o hidrogênio se difunde na direção
de menor temperatura, isto é, para cima na estrela.
Para a região central do Sol (![]() K,
K,
![]() g cm-3,
g cm-3,
![]() cm e
cm e
![]() e para um comprimento característico de difusão
de
e para um comprimento característico de difusão
de
![]() cm, o tempo
característico de difusão (equação
12) será
cm, o tempo
característico de difusão (equação
12) será
![]() anos.
Apesar desse tempo de difusão ser muito maior do que a idade
do Universo e, portanto, difusão ser irrelevante no Sol,
no caso de estrelas anãs brancas, a difusão
se dá em escalas de tempo de milhões de anos.
anos.
Apesar desse tempo de difusão ser muito maior do que a idade
do Universo e, portanto, difusão ser irrelevante no Sol,
no caso de estrelas anãs brancas, a difusão
se dá em escalas de tempo de milhões de anos.
Vamos, agora, considerar a difusão por pressão, que normalmente
é chamada de sedimentação ou deposição gravitacional.
Uma consideração estatística como no caso da difusão
por temperatura mostra que existe difusão mesmo nas
camadas isotérmicas, com um gradiente de pressão não-nulo.
Chapman e Cowling (1952), em seu livro The Mathematical Theory
of Non-Uniform Gases, Cambridge University Press, detalham como
obter ![]() , que não vamos reproduzir aqui, pois
C. Paquette, Claude Pelletier, Gilles Fontaine &
Georges Michaud, 1986, "Diffusion Coefficients for Stellar Plasma"
(Astrophysical Journal Supplement Series, 61, 177) discutem
que as aproximações introduzidas por Chapman e Cowling
para calcular os coeficientes de difusão analiticamente introduzem
erros sistemáticos, e calculam aproximações mais realísticas
estimando numericamente as integrais de colisão
usando o potencial Coulombiano com escudamento.
, que não vamos reproduzir aqui, pois
C. Paquette, Claude Pelletier, Gilles Fontaine &
Georges Michaud, 1986, "Diffusion Coefficients for Stellar Plasma"
(Astrophysical Journal Supplement Series, 61, 177) discutem
que as aproximações introduzidas por Chapman e Cowling
para calcular os coeficientes de difusão analiticamente introduzem
erros sistemáticos, e calculam aproximações mais realísticas
estimando numericamente as integrais de colisão
usando o potencial Coulombiano com escudamento.
Assumindo que um material consiste de dois componentes (1,2),
gases ideais com pesos moleculares ![]() e pressões
e pressões ![]() ,
podemos definir a escala de altura de pressão
,
podemos definir a escala de altura de pressão
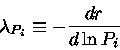 |
(23) |
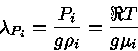 |
(24) |
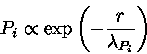 |
(25) |
As regiões convectivas têm um alto poder de mistura por movimentos turbulentos, em uma escala de tempo muito maior do que as mudanças causadas pelas reações nucleares e, portanto, podemos assumir que as regiões convectivas permanecem homogêneas:
| (26) |
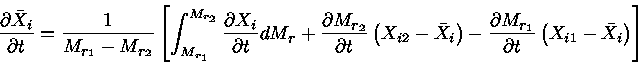 |
(27) |
Vittorio M. Canuto, em seu artigo de 2000 no Astrophysical Journal, Volume 534, p. L113-L115, ``Semiconvection and Overshooting: Schwarzschild and Ledoux Criteria Revisited'', discute a necessidade de se incluir estes efeitos. Paula Jofré e Achim Weiss mostram no seu artigo no Astronomy & Astrophysics de 2011, 533, 15, que se não levam em conta a difusão nas estrelas do halo na nossa Galáxia, a idade obtida é de 14 a 16 Ganos, incoerente com a idade do Universo. Quando levam em conta a difusão, como o hidrogênio difunde para cima, saindo do núcleo, existe menos combustível nuclear e a saída da sequência principal é mais rápida. Os coeficientes de difusão do H e do He foram publicados por Anne A. Thoul, Johm N. Bahcall & Abraham Loeb, no 1994,Astrophysical Journal, 421, 828. Neste caso a idade é de 10 a 12 Ganos, comprovando então que é necessário levar em conta a difusão na evolução estelar, especialmente para as estrelas de baixa metalicidade, que têm envelope convectivo razo e há difusão por um longo tempo. As isócronas Y2 (Yonsei-Yale: Pierre Demarque, Jong-Hak Woo, Yong-Cheol Kim & Sukyoung K. Yi, 2004, Astrophysical Journal Supplement Series, 155, 667) também incluem difusão de H e He, e também concordam com a idade de 10 a 12 Ganos. Os modelos PARSEC: PAdova and TRieste Stellar Evolution Code de Alessandro Bressan, Paola Marigo, Léo Girardi, Bernardo Salasnich, Claudia Dal Cero, Stefano Rubele & Ambra Nanni, publicados em 2012 no Monthly Notices of the Royal Astronomical Society, 427, 127, também incluem difusão na sequência principal.
A difusão, levando os elementos mais pesados para baixo, também faz com que a metalicidade observada hoje em dia não seja a metalicidade primordial. Existe ainda a levitação radiativa, que faz que elementos com bandas de absorção em comprimentos de onda de alto fluxo sejam carregados para as camadas externas, como o ferro, e terras raras nas estrelas Ap.