Se o interior estelar fosse isotérmico, a intensidade de radiação seria isotrópica, e não existiria um fluxo de radiação líquida em qualquer direção. De fato, entretanto, existe um gradiente radial de temperatura. Consequentemente se olharmos, de qualquer ponto do interior da estrela, na direção do centro, veremos um fluxo de radiação vindo da região abaixo, um pouco mais quente. Se olharmos para fora, veremos radiação vinda de uma região um pouco mais fria. O fluxo resultante de radiação é direcionado para fora.
Qual o valor deste fluxo? Isto depende da opacidade
dos gases. Se a opacidade for baixa, veremos, de um dado ponto,
até regiões bem mais quentes para dentro, e até
regiões bem mais frias para fora; a anisotropia da
radiação será grande, e o fluxo líquido
para fora será grande. Vamos representar a opacidade
por seu coeficiente de absorção por unidade de massa,
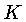, definido de forma que:
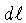. O
coeficiente de absorção no interior
estelar é da ordem de 1 cm2/g, e nunca muito menor. Se usarmos
novamente a densidade média do Sol como representativa,
vemos que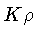 
é da ordem de um
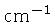, e portanto,
no interior das estrelas, uma distância da ordem de
1 cm é suficiente para absorver uma alta fração
da intensidade do feixe. De fato, uma espessura de vários
centímetros é completamente opaca. Não veremos
portanto muito longe, para dentro ou para fora, a partir
de qualquer ponto do interior da estrela. A diferença
de temperatura nesta pequena distância será da ordem
de um milésimo de um grau, já que a queda de temperatura
por todo o raio do Sol,
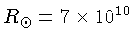cm, é de
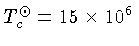K. O campo de radiação
portanto é muito aproximadamente isotrópico,
e poderíamos negligenciar esta pequena anisotropia, se o fluxo
não fosse a única forma de conectar os processos nucleares
no interior, com as perdas radiativas na superfície.