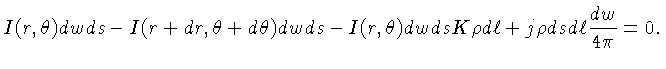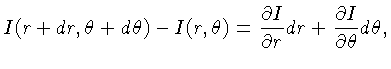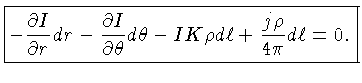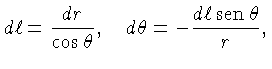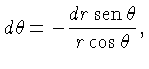Próxima: Equilíbrio Radiativo no Interior Estelar
Volta: Interiores Estelares
Anterior: O Transporte de Energia Radiativo
A Equação de Transporte Radiativo
Vamos derivar a relação entre o fluxo de radiação
e o gradiente de temperatura. Descrevendo o campo
de radiação por sua intensidade
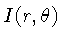 ,
energia por unidade de área, por unidade de tempo,
e por unidade de ângulo sólido (esferorradiano), a uma distância
,
energia por unidade de área, por unidade de tempo,
e por unidade de ângulo sólido (esferorradiano), a uma distância
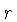 do centro da estrela, e em uma direção
inclinada de um ângulo
do centro da estrela, e em uma direção
inclinada de um ângulo 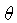 do raio vetor.
do raio vetor.
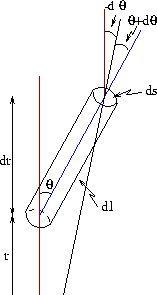
Figura 1.4:
Intensidade e Ângulo Sólido
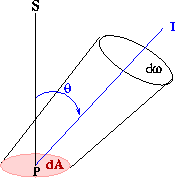 |
Considere os ganhos e perdas que a radiação sofre,
dentro de um ângulo sólido 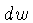 , por unidade de tempo,
em um cilindro com seção de choque
, por unidade de tempo,
em um cilindro com seção de choque 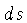 e comprimento
e comprimento
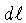 , equivalente ao raio vetor
, equivalente ao raio vetor 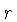 , e
, e 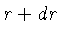 . A
intensidade de radiação entrando pela base será:
enquanto a perda correspondente na superfície
superior será:
Na última expressão, o incremento em
. A
intensidade de radiação entrando pela base será:
enquanto a perda correspondente na superfície
superior será:
Na última expressão, o incremento em 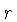 ocorre
porque o topo do cilindro está mais longe do centro
do que a base, e o incremento em
ocorre
porque o topo do cilindro está mais longe do centro
do que a base, e o incremento em 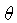 ocorre porque
a curvatura introduzida pela simetria esférica leva
o topo vertical do cilindro a estar inclinado em
relação à base.
ocorre porque
a curvatura introduzida pela simetria esférica leva
o topo vertical do cilindro a estar inclinado em
relação à base.
A perda de energia por unidade de tempo
por absorção sobre o comprimento do cilindro
será de:
Finalmente, precisamos incluir a emissão dos gases
no cilindro. Seja 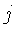 a energia total emitida, por unidade
de massa, por unidade de tempo, isotropicamente em todas as direções.
A emissão de toda a matéria no cilindro, na direção
contida pelo ângulo sólido
a energia total emitida, por unidade
de massa, por unidade de tempo, isotropicamente em todas as direções.
A emissão de toda a matéria no cilindro, na direção
contida pelo ângulo sólido 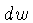 será então:
Se aplicarmos a condição de equilíbrio térmico
especificamente para o campo de radiação, exigimos
que os ganhos da radiação balancem exatamente as
perdas, isto é, que a soma dos termos seja nula:
Como, para um elemento infinitesimal:
assumindo
será então:
Se aplicarmos a condição de equilíbrio térmico
especificamente para o campo de radiação, exigimos
que os ganhos da radiação balancem exatamente as
perdas, isto é, que a soma dos termos seja nula:
Como, para um elemento infinitesimal:
assumindo
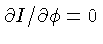 , e simplificando
, e simplificando 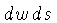 em todos os termos,
obtemos
Usando as relações geométricas:
obtemos
em todos os termos,
obtemos
Usando as relações geométricas:
obtemos
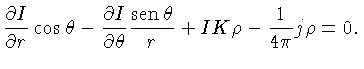 |
(1.36) |
Esta é a equação básica de transporte radiativo, que precisa
ser obedecida a cada ponto da estrela.





Próxima: Equilíbrio Radiativo no Interior Estelar
Volta: Interiores Estelares
Anterior: O Transporte de Energia Radiativo
©
Modificada em 4 set 2001
![]() ,
energia por unidade de área, por unidade de tempo,
e por unidade de ângulo sólido (esferorradiano), a uma distância
,
energia por unidade de área, por unidade de tempo,
e por unidade de ângulo sólido (esferorradiano), a uma distância
![]() do centro da estrela, e em uma direção
inclinada de um ângulo
do centro da estrela, e em uma direção
inclinada de um ângulo ![]() do raio vetor.
do raio vetor.