Se um elétron de carga ![]() , movendo-se não-relativisticamente, passa
por um íon de carga
, movendo-se não-relativisticamente, passa
por um íon de carga ![]() , ele é acelerado e
irradia de acordo com o
resultado de Larmor
[Sir Joseph Larmor (1857-1942)]:
, ele é acelerado e
irradia de acordo com o
resultado de Larmor
[Sir Joseph Larmor (1857-1942)]:
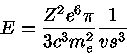 |
(1.63b) |
Para as transições livre-livre
(desaceleração ou bremstrahlung), a fórmula de Kramers
pode ser expressa considerando-se um íon de carga nuclear
efetiva
![]() , em um meio com
, em um meio com ![]() elétrons livres
por unidade de volume com momenta entre
elétrons livres
por unidade de volume com momenta entre ![]() e
e ![]() , em relação
ao íon. O coeficiente de absorção livre-livre ( free-free)
por íon, para absorção da radiação de frequência
, em relação
ao íon. O coeficiente de absorção livre-livre ( free-free)
por íon, para absorção da radiação de frequência
![]() pelos
pelos ![]() elétrons livres com momentum no intervalo
relevante, é dado pela fórmula de Kramers:
elétrons livres com momentum no intervalo
relevante, é dado pela fórmula de Kramers:
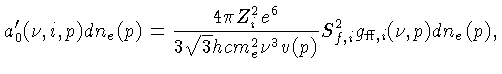
Seja yei o número de elétrons livres, por átomo, provenientes
de um átomo de carga nuclear Zie. Nesse caso,
| Sf,i = |
yei Zi |
Para
h![]() <kT
e maior do que a
freqüência de plasma
<kT
e maior do que a
freqüência de plasma
![$g_{ff}=\frac{\sqrt{3}}{\pi}\[\ln\frac{(2kT)^\frac{3}{2}} {\pi e^2 \nu m_e^{\frac{1}{2}}}-\frac{5\gamma}{2}]$](imggf1.gif)
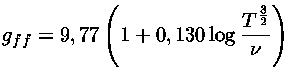
Para obter o coeficiente de absorção livre-livre por átomo,
precisamos integrar a equação anterior sobre todos os momenta
possíveis. Utilizando a distribuição de momentum de
Fermi-Dirac, obtém-se:
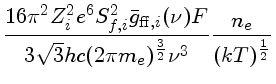 |
(1.64) |
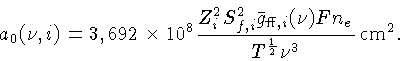
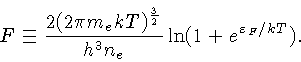
O artigo Temperature-averaged and total free-free Gaunt factors for K and Maxwellian distributions of electrons (Corrigendum), de Miguel A. de Avillez e Dieter Breitschwerdt, pu_licado no Astronomy & Astrophysics, 620, C1 (2018) traz tabelas do fator de Gaunt livre-livre.