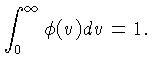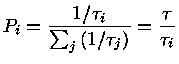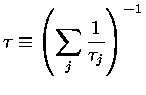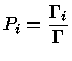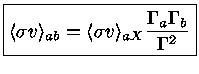Próxima: Reações Não-Ressonantes
Volta: Geração de Energia Nuclear
Anterior: Geração de Energia Nuclear
O equilíbrio energético nos dá a energia liberada
em cada reação nuclear;
se considerarmos a reação genérica
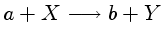 |
(1.67) |
o princípio de conservação de energia
demanda a igualidade:
onde
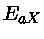 é a energia cinética do centro de massa
de
é a energia cinética do centro de massa
de 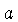 e
e 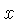 , e
, e 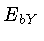 é energia cinética do centro de massa
de
é energia cinética do centro de massa
de 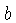 e
e 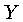 .
Com a energia liberada por reação,
e com o número de reações por unidade de volume
por segundo,
podemos calcular a energia liberada por unidade de volume
por segundo. Para isto, precisamos definir a seção
de choque da reação,
.
Com a energia liberada por reação,
e com o número de reações por unidade de volume
por segundo,
podemos calcular a energia liberada por unidade de volume
por segundo. Para isto, precisamos definir a seção
de choque da reação, 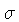 . A seção de choque
é uma medida da probabilidade de ocorrência da reação,
por par de partículas. Na nossa reação genérica,
em que um núcleo
. A seção de choque
é uma medida da probabilidade de ocorrência da reação,
por par de partículas. Na nossa reação genérica,
em que um núcleo 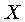 é bombardeado por um fluxo uniforme
de partícula
é bombardeado por um fluxo uniforme
de partícula 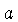 , a seção de choque é
definida como:
O nome seção de choque advém da unidade, área, e porque
o número de reações pode ser calculado assumindo-se que
o núcleo
, a seção de choque é
definida como:
O nome seção de choque advém da unidade, área, e porque
o número de reações pode ser calculado assumindo-se que
o núcleo 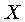 tem uma área
tem uma área 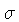 e que uma reação ocorre
sempre que uma partícula
e que uma reação ocorre
sempre que uma partícula 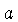 atinge aquela área.
atinge aquela área.
Supondo que o núcleo 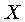 tem uma densidade numérica
tem uma densidade numérica 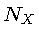 , a taxa de reação
por unidade de volume será dada pelo produto
, a taxa de reação
por unidade de volume será dada pelo produto
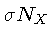 e pelo fluxo
de partículas
e pelo fluxo
de partículas 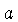 . Supondo que o fluxo de partículas
. Supondo que o fluxo de partículas 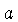 é dado pela translação uniforme, com velocidade
é dado pela translação uniforme, com velocidade 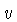 , de
partículas com densidade
, de
partículas com densidade 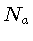 , ou seja, o fluxo é
, ou seja, o fluxo é 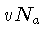 .
A taxa de reações será então dada por
.
A taxa de reações será então dada por
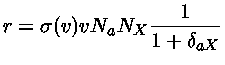
| (1.68) |
onde
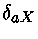 é o delta de Kronecker
[Leopold Kronecker (1823-1891)]
(
é o delta de Kronecker
[Leopold Kronecker (1823-1891)]
(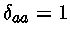 ,
,
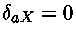 ,
se
,
se 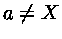 ).
Este último fator leva em conta que não devemos
contar duplamente as partículas idênticas.
).
Este último fator leva em conta que não devemos
contar duplamente as partículas idênticas.
A velocidade 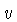 é a velocidade relativa entre as partículas
é a velocidade relativa entre as partículas 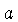 e
e 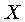 .
Se o gás estiver em equilíbrio termodinâmico, existe
um espectro de velocidades
.
Se o gás estiver em equilíbrio termodinâmico, existe
um espectro de velocidades 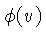 , definido de modo que
Neste caso,
, definido de modo que
Neste caso, 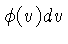 representa a probabilidade que a velocidade
relativa esteja no intervalo
representa a probabilidade que a velocidade
relativa esteja no intervalo 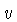 e
e 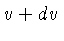 , e a taxa de reação
total, por unidade de volume será dada por:
, e a taxa de reação
total, por unidade de volume será dada por:
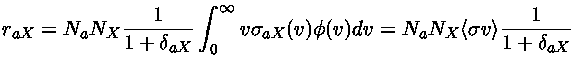
|
(1.69) |
Como um estado 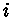 com uma largura energética natural
com uma largura energética natural 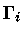 ,
pelo princípio da incerteza, decai em um tempo
,
pelo princípio da incerteza, decai em um tempo 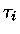 ,
definido como
,
definido como
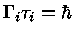 |
(1.69a) |
a probabilidade de decaimento pelo canal 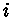 é dada por:
é dada por:
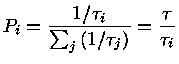 |
(1.69b) |
onde
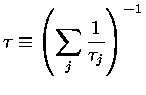 |
(1.69c) |
é o tempo de vida médio total do estado com largura natural
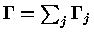 ; de modo que a probabilidade de
decaimento pelo canal
; de modo que a probabilidade de
decaimento pelo canal 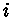 pode ser expressa como:
pode ser expressa como:
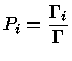 |
(1.69d) |
Portanto, o fator
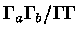 nos dá a probabilidade
de reagir
nos dá a probabilidade
de reagir 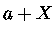 , resultando em
, resultando em 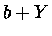 .
.
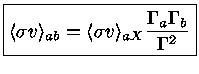 |
(1.69e) |





Próxima: Reações Não-Ressonantes
Volta: Geração de Energia Nuclear
Anterior: Geração de Energia Nuclear
©
Modificada em 20 set 2001

![]() tem uma densidade numérica
tem uma densidade numérica ![]() , a taxa de reação
por unidade de volume será dada pelo produto
, a taxa de reação
por unidade de volume será dada pelo produto
![]() e pelo fluxo
de partículas
e pelo fluxo
de partículas ![]() . Supondo que o fluxo de partículas
. Supondo que o fluxo de partículas ![]() é dado pela translação uniforme, com velocidade
é dado pela translação uniforme, com velocidade ![]() , de
partículas com densidade
, de
partículas com densidade ![]() , ou seja, o fluxo é
, ou seja, o fluxo é ![]() .
A taxa de reações será então dada por
.
A taxa de reações será então dada por