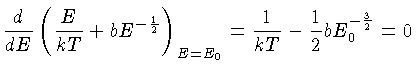Próxima: Reações Ressonantes
Volta: Geração de Energia Nuclear
Anterior: Seção de Choque e Taxa de
O raio de um núcleo de massa atômica 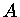 pode ser representado
por
pode ser representado
por
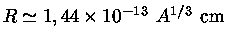 |
(1.69f) |
Para uma reação 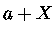 ,
,
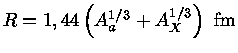 |
(1.69g) |
onde fm é um fentometro, também chamado de um fermi,
e corresponde a 10-13 cm.
Para que uma reação nuclear ocorra, as partículas
precisam vencer a barreira Coulombiana
[Charles Augustin de Coulomb (1736-1806)]
repulsiva entre as
partículas, dada por
onde K=1 no sistema cgs,
enquanto que a energia cinética entre as partículas
é determinada por uma distribuição de velocidades de
Maxwell-Boltzmann correspondente à energia térmica
Para temperaturas da ordem de dezenas a centenas de milhões
de graus, a energia média das partículas
interagentes são
muitas ordens de magnitudes menores
do que a barreira Coulombiana que as separa.
As reações ocorrem pelo efeito de tunelamento quântico, proposto em 1928
pelo físico russo-americano George Antonovich Gamow (1904-1968).
As partículas
com maior chance de penetrar a barreira são aquelas com
a máxima energia na distribuição de Maxwell-Boltzmann:
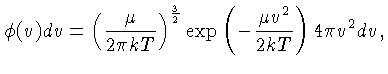 |
(1.70) |
onde 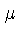 é a massa reduzida das partículas
é a massa reduzida das partículas 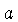 e
e 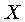 .
Entretanto, a distribuição de Maxwell-Boltzmann mostra
que o
número de pares de partículas com energia
muito acima de
.
Entretanto, a distribuição de Maxwell-Boltzmann mostra
que o
número de pares de partículas com energia
muito acima de 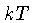 decresce rapidamente com a energia.
George Gamow foi o primeiro a demonstrar que a probabilidade
de duas partículas de carga
decresce rapidamente com a energia.
George Gamow foi o primeiro a demonstrar que a probabilidade
de duas partículas de carga 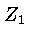 e
e 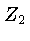 , movendo-se
com velocidade relativa
, movendo-se
com velocidade relativa 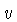 , penetrar sua repulsão
eletrostática é proporcional ao fator
, penetrar sua repulsão
eletrostática é proporcional ao fator
Penetração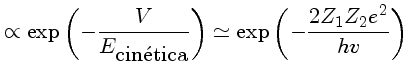 |
(1.71) |
já que
pelo Princípio da Incerteza
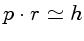 .
.
 As seções de choque para reações nucleares serão
proporcionais a esse fator, pois as reações dificilmente
podem ocorrer se as partículas não penetrarem essa
barreira. Esse fator de penetração pode ser
obtido pelo método WKB
[Gregor Wentzel (1898-1978),
Hendrik Anthony Kramers (1894-1952)
e Marcel Louis Brillouin (1854-1948)], válido para o caso de energia
da barreira muito maior do que a energia média das partículas.
O fator dentro da exponencial chama-se fator de Sommerfeld [Arnold
Johannes Wilhelm Sommerfeld (1868-1951)].
As seções de choque para reações nucleares serão
proporcionais a esse fator, pois as reações dificilmente
podem ocorrer se as partículas não penetrarem essa
barreira. Esse fator de penetração pode ser
obtido pelo método WKB
[Gregor Wentzel (1898-1978),
Hendrik Anthony Kramers (1894-1952)
e Marcel Louis Brillouin (1854-1948)], válido para o caso de energia
da barreira muito maior do que a energia média das partículas.
O fator dentro da exponencial chama-se fator de Sommerfeld [Arnold
Johannes Wilhelm Sommerfeld (1868-1951)].
Penetração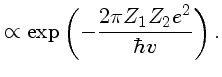 |
(1.71a) |
A interação entre duas partículas também
é proporcional ao fator quantum-geométrico
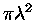 ,
onde
,
onde 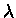 é o comprimento de onda de de Broglie:
é o comprimento de onda de de Broglie:
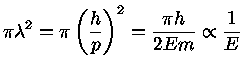 |
(1.72) |
pois, para um parâmetro de aproximação (distância mínima)
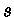 , o momentum angular quantizado é
, o momentum angular quantizado é
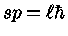 , e a seção
de choque passando de um estado
, e a seção
de choque passando de um estado 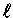 para
para 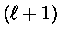 é dada
por
é dada
por
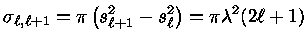 |
(1.72a) |
Em baixa energia, tanto (1.71) quanto (1.72)
variam rapidamente com a energia. Com essas motivações,
definimos a seção de choque a baixas energias como
um produto de três fatores dependentes da energia:
onde
e 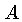 é o peso atômico reduzido
O fator
é o peso atômico reduzido
O fator 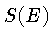 representa a parte nuclear da probabilidade de ocorrência
da reação, enquanto os outros dois fatores representam
dependências não-nucleares, bem conhecidas.
O fator
representa a parte nuclear da probabilidade de ocorrência
da reação, enquanto os outros dois fatores representam
dependências não-nucleares, bem conhecidas.
O fator 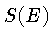 é normalmente constante ou fracamente dependente da energia
sobre uma faixa limitada de energias.
é normalmente constante ou fracamente dependente da energia
sobre uma faixa limitada de energias.
A distribuição de velocidades de Maxwell-Boltzmann pode ser
escrita em termos da distribuição de energia:
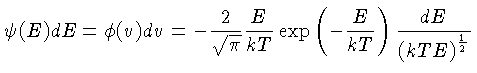 |
(1.74) |
e
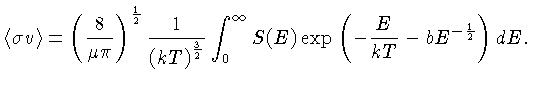 |
(1.75) |
O fator
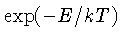 decresce para altas energias, enquanto que o fator
decresce para altas energias, enquanto que o fator
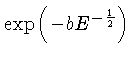 decresce para baixas energias.
As reações são mais efetivas para uma energia
decresce para baixas energias.
As reações são mais efetivas para uma energia 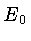 determinada
pelo máximo do integrando:
ou
determinada
pelo máximo do integrando:
ou
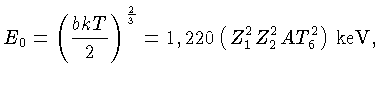 |
(1.76) |
onde 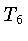 é a temperatura em milhões de graus Kelvin, e
é a temperatura em milhões de graus Kelvin, e
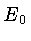 é chamada de energia efetiva para a reação nuclear.
Pela equação (1.76),
podemos calcular que
a energia efetiva para a reação nuclear para partículas
leves e temperaturas de algumas dezenas de milhões de graus,
obtendo
é chamada de energia efetiva para a reação nuclear.
Pela equação (1.76),
podemos calcular que
a energia efetiva para a reação nuclear para partículas
leves e temperaturas de algumas dezenas de milhões de graus,
obtendo
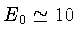 a 30 keV, enquanto que a energia térmica
é de
a 30 keV, enquanto que a energia térmica
é de
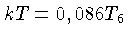 keV, refletindo o fato que a penetração
da barreira Coulombiana favorece as partículas de alta energia
da distribuição de Maxwell-Boltzmann.
keV, refletindo o fato que a penetração
da barreira Coulombiana favorece as partículas de alta energia
da distribuição de Maxwell-Boltzmann.





Próxima: Reações Ressonantes
Volta: Geração de Energia Nuclear
Anterior: Seção de Choque e Taxa de
©
Modificada em 17 abril 2006
![]() pode ser representado
por
pode ser representado
por
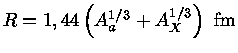
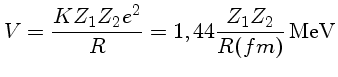
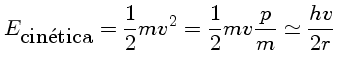
 As seções de choque para reações nucleares serão
proporcionais a esse fator, pois as reações dificilmente
podem ocorrer se as partículas não penetrarem essa
barreira. Esse fator de penetração pode ser
obtido pelo método WKB
[Gregor Wentzel (1898-1978),
Hendrik Anthony Kramers (1894-1952)
e Marcel Louis Brillouin (1854-1948)], válido para o caso de energia
da barreira muito maior do que a energia média das partículas.
O fator dentro da exponencial chama-se fator de Sommerfeld [Arnold
Johannes Wilhelm Sommerfeld (1868-1951)].
As seções de choque para reações nucleares serão
proporcionais a esse fator, pois as reações dificilmente
podem ocorrer se as partículas não penetrarem essa
barreira. Esse fator de penetração pode ser
obtido pelo método WKB
[Gregor Wentzel (1898-1978),
Hendrik Anthony Kramers (1894-1952)
e Marcel Louis Brillouin (1854-1948)], válido para o caso de energia
da barreira muito maior do que a energia média das partículas.
O fator dentro da exponencial chama-se fator de Sommerfeld [Arnold
Johannes Wilhelm Sommerfeld (1868-1951)].
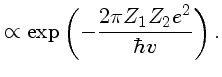
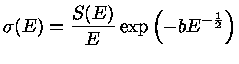
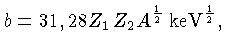
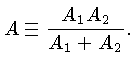
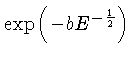 decresce para baixas energias.
As reações são mais efetivas para uma energia
decresce para baixas energias.
As reações são mais efetivas para uma energia