




Próxima: Novas e Supernovas
Volta: Anãs Brancas
Anterior: Cristalização
As observações de James W. Liebert (1946-),
Conard C. Dahn
e David G. Monet em 1988
mostram que as anãs brancas vão ficando cada vez mais raras
quando a temperatura efetiva é menor do que 5000 K, e
finalmente quando
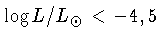 , não há mais nenhuma anã branca observada.
O tempo de esfriamento das anãs brancas até estas
baixas luminosidades e temperaturas é maior do que a idade
do disco de nossa Galáxia, de modo que mesmo as
anãs brancas formadas na primeira geração de estrelas
ainda estão visíveis.
O halo é cerca de 2 bilhões de anos mais velho e as anãs brancas acima
de 0,8 massas solares já estão mais fracas que o limite de detecção
do Telescópio Espacial Hubble, mesmo para aquelas que estão nos
aglomerados globulares mais próximos.
, não há mais nenhuma anã branca observada.
O tempo de esfriamento das anãs brancas até estas
baixas luminosidades e temperaturas é maior do que a idade
do disco de nossa Galáxia, de modo que mesmo as
anãs brancas formadas na primeira geração de estrelas
ainda estão visíveis.
O halo é cerca de 2 bilhões de anos mais velho e as anãs brancas acima
de 0,8 massas solares já estão mais fracas que o limite de detecção
do Telescópio Espacial Hubble, mesmo para aquelas que estão nos
aglomerados globulares mais próximos.
Para estimar a função luminosidade a partir de observações limitadas em
magnitude, é preciso corrigir cada observação pelo inverso do volume que aquela
magnitude pode ser observada [Maarten Schmidt (1929-), 1968, Astrophysical Journal, 151, 393], considerando-se as magnitudes mínimas
e máximas das observações:
onde
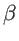 é a fração do céu observada,
é a fração do céu observada,
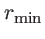 é devido à magnitude máxima observada,
de saturação do instrumento,
e
é devido à magnitude máxima observada,
de saturação do instrumento,
e 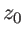 é a escala de altura do disco da Galáxia.
é a escala de altura do disco da Galáxia.
O decréscimo no número de anãs brancas para baixas luminosidades
representa um decréscimo na função luminosidade --
a densidade espacial de anãs brancas, por intervalo
de magnitude bolométrica absoluta (número 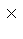 luminosidade) --
foi primeiro explicado em 1987 por
Donald Earl Winget (1955-),
Carl John Hansen (1933-2011),
Hugh M. Van Horn (1938-),
Gilles Fontaine (1948-),
R. Edward Nather (1926-2014),
Kepler de Souza Oliveira Filho (1956-)
e Donald Quincy Lamb (1945-),
em termos da idade finita da
disco local da nossa Galáxia,
de cerca de 9 Ganos.
luminosidade) --
foi primeiro explicado em 1987 por
Donald Earl Winget (1955-),
Carl John Hansen (1933-2011),
Hugh M. Van Horn (1938-),
Gilles Fontaine (1948-),
R. Edward Nather (1926-2014),
Kepler de Souza Oliveira Filho (1956-)
e Donald Quincy Lamb (1945-),
em termos da idade finita da
disco local da nossa Galáxia,
de cerca de 9 Ganos.
James Liebert, Pierre Bergeron & Jay B. Holberg, em 2005, no artigo
publicado no Astrophysical Journal Supplement, 156, 47
e
Hugh C. Harris et al., em 2006, no artigo publicado no
Astronomical Journal, 131, 571, confirmam o decréscimo do número de anãs
brancas abaixo de 4500K para conjuntos maiores de anãs brancas.
A função luminosidade teórica é dada por
(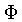 , em unidades de
, em unidades de
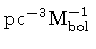 ):
):
onde 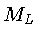 e
e 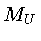 ,
, 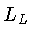 e
e 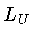 são os limites
inferiores e superiores das massas e luminosidades
das estrelas na sequência principal que produzem
anãs brancas observáveis, respectivamente.
O limite inferior para a massa é o turn-off point
da sequência principal
para a idade do disco
(
são os limites
inferiores e superiores das massas e luminosidades
das estrelas na sequência principal que produzem
anãs brancas observáveis, respectivamente.
O limite inferior para a massa é o turn-off point
da sequência principal
para a idade do disco
(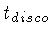 ), obtida integrando-se
), obtida integrando-se
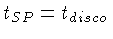 .
A luminosidade superior é de cerca de
.
A luminosidade superior é de cerca de
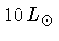 , e a luminosidade
inferior é obtida para uma idade:
Outros valores necessários incluem a
taxa de formação estelar
(SFR) como função do tempo,
, e a luminosidade
inferior é obtida para uma idade:
Outros valores necessários incluem a
taxa de formação estelar
(SFR) como função do tempo,
![$ [SFR\equiv\psi(t)]$](img758.gif) , a função inicial de massa
, a função inicial de massa
![$ [IMF\equiv\phi(t)]$](img759.gif) , a relação massa inicial
, a relação massa inicial
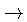 massa final
massa final
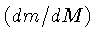 , e naturalmente a taxa de esfriamento das anãs brancas,
que depende da massa.
, e naturalmente a taxa de esfriamento das anãs brancas,
que depende da massa.
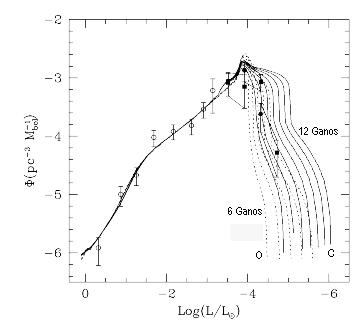
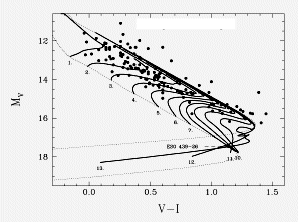
 Função luminosidade das anãs brancas, calculada por
Matthew Allan Wood (1961-) para idades do disco
da nossa Galáxia entre 6 (linha à esquerda) e 12 Ganos
(linha à direita). Os modelos de anãs brancas têm
núcleo de carbono
(linha contínua) e oxigênio (linha pontilhada),
e os pontos são as observações
de James W. Liebert (1946-), Conard Dahn e David Monet de 1988.
As caixas, em baixa luminosidade, indicam a incerteza nos dados.
As curvas que passam pela caixa de mais baixa luminosidade
têm idade entre 6,5 e 8,5 Ganos, se as anãs brancas têm núcleo
de oxigênio, e entre 8,5 e 11 Ganos, se têm núcleo de carbono.
A incerteza na composição do núcleo se deve à
incerteza na taxa de reação nuclear
C(
Função luminosidade das anãs brancas, calculada por
Matthew Allan Wood (1961-) para idades do disco
da nossa Galáxia entre 6 (linha à esquerda) e 12 Ganos
(linha à direita). Os modelos de anãs brancas têm
núcleo de carbono
(linha contínua) e oxigênio (linha pontilhada),
e os pontos são as observações
de James W. Liebert (1946-), Conard Dahn e David Monet de 1988.
As caixas, em baixa luminosidade, indicam a incerteza nos dados.
As curvas que passam pela caixa de mais baixa luminosidade
têm idade entre 6,5 e 8,5 Ganos, se as anãs brancas têm núcleo
de oxigênio, e entre 8,5 e 11 Ganos, se têm núcleo de carbono.
A incerteza na composição do núcleo se deve à
incerteza na taxa de reação nuclear
C(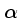 ,
,
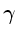 )O.
)O.
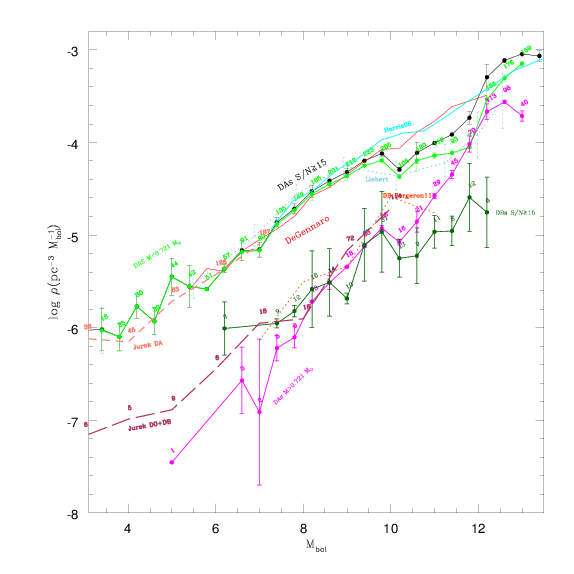
Função de luminosidade para anãs brancas identificadas espectroscopicamente no
Data Release 7 do Sloan Digital Sky Survey, de acordo com
Kepler de Souza Oliveira Filho, publicado no artigo
Mass Distribution and Luminosity Functions for DAs and DBs, no
Proceedings of
18th European White Dwarf Workshop,
editores Jerzy Krzesinski, G. Stachowski, Pawel Moskalik, & K. Bajan,
Astronomical Society of the Pacific Conference Proceedings, Vol. 469, p.83-87.
 Modelos de estrelas anãs brancas
de acordo com os cálculos de Gilles Fontaine (1948-), Pierre Brassard e
Pierre Bergeron, da Université de Montréal, no Canadá,
publicados
em 2001 no Publications of the Astronomical Society of the Pacific,
113, 409.
Modelos de estrelas anãs brancas
de acordo com os cálculos de Gilles Fontaine (1948-), Pierre Brassard e
Pierre Bergeron, da Université de Montréal, no Canadá,
publicados
em 2001 no Publications of the Astronomical Society of the Pacific,
113, 409.
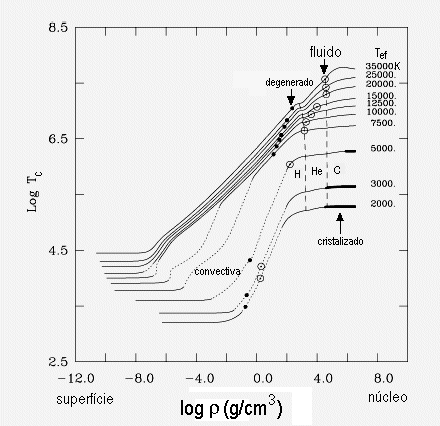 Evolução da estrutura do modelo de uma anã branca com 0,6 MSol,
durante seu esfriamento desde
Tef=35 000K (curva superior) até
Tef=2 000K (curva inferior). Os modelos evolucionários
incluem o envelope até uma profundidade ótica
τ≥10-8. Cada porção
sólida indica a região radiativa,
a parte pontilhada a convectiva e a parte tracejada a cristalizada
(Γ≥180).
O topo da camada convectiva está sempre na fotosfera. Os elétrons
estão degenerados à direita do ponto escuro em cada curva. O
círculo aberto indica a região em que os íons tornam-se correlacionados
(Γ≥1, fase fluída). As linhas tracejadas indicam as zonas de transição
de composição química, de H/He para baixas densidades e de
He/C para mais altas densidades. Estes modelos foram calculados com
núcleos somente de carbono, enquanto na realidade as anãs brancas
têm núcleos de C e O, mas cuja fração depende da
taxa C(α,γ)O.
Note que embora o núcleo de C compreenda somente uma parte de cada curva,
ele corresponde a 99% da massa da estrela (72% do raio).
Embora a condução seja dominante no núcleo degenerado, as curvas
mostram que o núcleo de uma anã branca nunca fica realmente isotérmico.
Os modelos evolucionários indicam que a máxima quantidade
de hélio
que sobrevive a fase quente de núcleo de nebulosa planetária
é de 10-2 da massa total (18% do raio) da estrela e que a máxima massa
em hidrogênio é de 10-4 da massa da estrela (10% do raio).
Evolução da estrutura do modelo de uma anã branca com 0,6 MSol,
durante seu esfriamento desde
Tef=35 000K (curva superior) até
Tef=2 000K (curva inferior). Os modelos evolucionários
incluem o envelope até uma profundidade ótica
τ≥10-8. Cada porção
sólida indica a região radiativa,
a parte pontilhada a convectiva e a parte tracejada a cristalizada
(Γ≥180).
O topo da camada convectiva está sempre na fotosfera. Os elétrons
estão degenerados à direita do ponto escuro em cada curva. O
círculo aberto indica a região em que os íons tornam-se correlacionados
(Γ≥1, fase fluída). As linhas tracejadas indicam as zonas de transição
de composição química, de H/He para baixas densidades e de
He/C para mais altas densidades. Estes modelos foram calculados com
núcleos somente de carbono, enquanto na realidade as anãs brancas
têm núcleos de C e O, mas cuja fração depende da
taxa C(α,γ)O.
Note que embora o núcleo de C compreenda somente uma parte de cada curva,
ele corresponde a 99% da massa da estrela (72% do raio).
Embora a condução seja dominante no núcleo degenerado, as curvas
mostram que o núcleo de uma anã branca nunca fica realmente isotérmico.
Os modelos evolucionários indicam que a máxima quantidade
de hélio
que sobrevive a fase quente de núcleo de nebulosa planetária
é de 10-2 da massa total (18% do raio) da estrela e que a máxima massa
em hidrogênio é de 10-4 da massa da estrela (10% do raio).
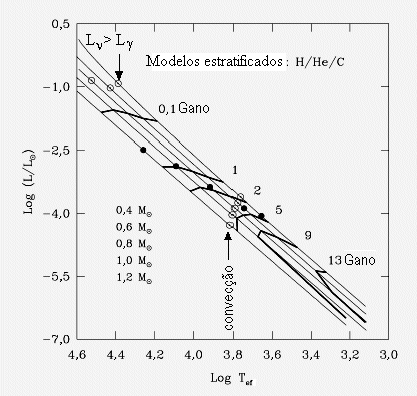 Curvas evolucionárias para modelos com 0,4; 0,6; 0,8; 1,0 e 1,2 MSol,
de cima para baixo. As curvas mais grossas indicam as isócronas, com
o tempo de esfriamento em unidades de Ganos.
Os pontos escuros indicam o início da cristalização no centro
do modelo (com Γ≈180). Os círculos abertos em altas temperaturas (esquerda)
indicam a transição de esfriamento dominado por neutrinos, em temperaturas
mais altas, para esfriamento dominado por radiação, para
temperaturas mais baixas. Os círculos abertos no meio do diagrama
indicam o início do acoplamento convectivo entre o envelope e o
núcleo. Este acoplamento, quando a zona de convecção atmosférica
chega ao núcleo provoca uma mudança acentuada na taxa de
esfriamento, já que a convecção transporta o calor do núcleo
muito mais efetivamente do que o envelope radiativo existente
até então. Este efeito provoca o aumento no número de anãs
brancas observadas nesta temperatura efetiva, como veremos no
gráfico da função luminosidade.
Curvas evolucionárias para modelos com 0,4; 0,6; 0,8; 1,0 e 1,2 MSol,
de cima para baixo. As curvas mais grossas indicam as isócronas, com
o tempo de esfriamento em unidades de Ganos.
Os pontos escuros indicam o início da cristalização no centro
do modelo (com Γ≈180). Os círculos abertos em altas temperaturas (esquerda)
indicam a transição de esfriamento dominado por neutrinos, em temperaturas
mais altas, para esfriamento dominado por radiação, para
temperaturas mais baixas. Os círculos abertos no meio do diagrama
indicam o início do acoplamento convectivo entre o envelope e o
núcleo. Este acoplamento, quando a zona de convecção atmosférica
chega ao núcleo provoca uma mudança acentuada na taxa de
esfriamento, já que a convecção transporta o calor do núcleo
muito mais efetivamente do que o envelope radiativo existente
até então. Este efeito provoca o aumento no número de anãs
brancas observadas nesta temperatura efetiva, como veremos no
gráfico da função luminosidade.
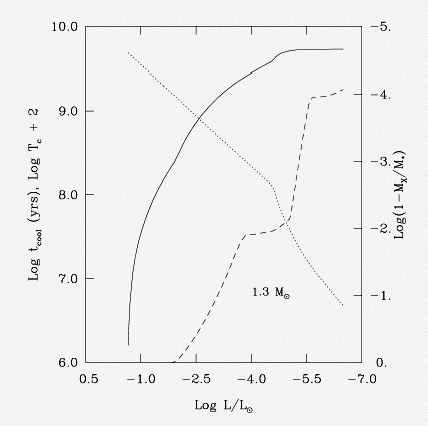 A linha sólida mostra a curva de esfriamento
(log tcool × log L/LSol) para um
modelo de 1,3 MSol. A linha tracejada mostra a
progressão da frente de cristalização
(com Γ≈180) desde o centro até a
base da camada de H. A posição da frente está expressa no
lado direito do gráfico. Os plateaus correspondem às
zonas de transição de composição química: a de C/He próximo
a log(1-MX/M*)=-2, já que os
modelos têm uma camada de He de 10-2 M*.
A transição de He/H está em
log(1-MX/M*)=-4, já que os
modelos têm uma camada de H de 10-4 M*.
A linha pontilhada ilustra a relação L-Tc no modelo.
A linha sólida mostra a curva de esfriamento
(log tcool × log L/LSol) para um
modelo de 1,3 MSol. A linha tracejada mostra a
progressão da frente de cristalização
(com Γ≈180) desde o centro até a
base da camada de H. A posição da frente está expressa no
lado direito do gráfico. Os plateaus correspondem às
zonas de transição de composição química: a de C/He próximo
a log(1-MX/M*)=-2, já que os
modelos têm uma camada de He de 10-2 M*.
A transição de He/H está em
log(1-MX/M*)=-4, já que os
modelos têm uma camada de H de 10-4 M*.
A linha pontilhada ilustra a relação L-Tc no modelo.
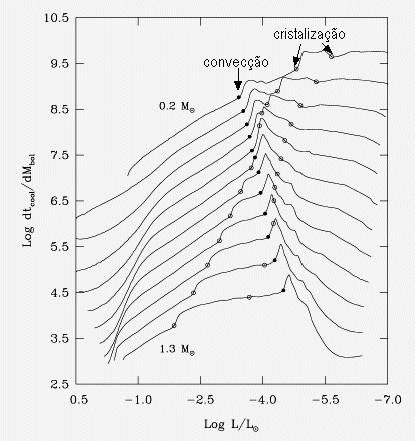 Curvas evolucionárias de 12 modelos com massas entre 0,2 e 1,3 MSol,
de cima para baixo. Todas as curvas, exceto a de 0,2 MSol,
estão deslocadas para baixo para visualização. O círculo
aberto em maior luminosidade corresponde ao início da cristalização
no centro
(com Γ≈180) e o segundo quando 98% da massa está cristalizada. O
ponto escuro indica quando inicia o acoplamento convectivo,
isto é, quando a zona de convecção superficial atinge o
núcleo. A liberação do excesso de energia térmica associada
ao acoplamento convectivo é maior do que o efeito
da liberação do calor latente de cristalização.
Curvas evolucionárias de 12 modelos com massas entre 0,2 e 1,3 MSol,
de cima para baixo. Todas as curvas, exceto a de 0,2 MSol,
estão deslocadas para baixo para visualização. O círculo
aberto em maior luminosidade corresponde ao início da cristalização
no centro
(com Γ≈180) e o segundo quando 98% da massa está cristalizada. O
ponto escuro indica quando inicia o acoplamento convectivo,
isto é, quando a zona de convecção superficial atinge o
núcleo. A liberação do excesso de energia térmica associada
ao acoplamento convectivo é maior do que o efeito
da liberação do calor latente de cristalização.
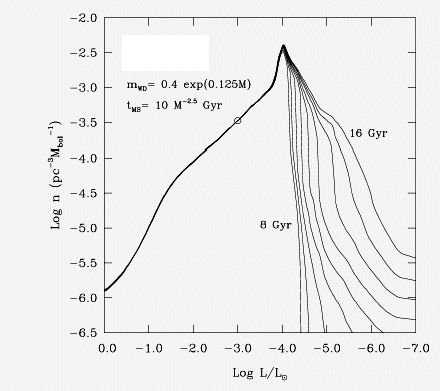 Funções de luminoside calculadas para um modelo do disco galáctico,
assumindo taxa de formação estelar constante e função inicial
de massa de Salpeter [Edwin Ernest Salpeter (1925-2008)]
(IMF ∝
M-2,35).
O tempo de vida na sequência principal está assumido como
tMS = 10-2,5 Ganos.
As curvas foram normalizadas no ponto indicado pelo círculo.
O pico em L/LSol~10-4 corresponde ao
acúmulo de anãs brancas devido à liberação de calor
por cristalização e acoplamento convectivo.
Funções de luminoside calculadas para um modelo do disco galáctico,
assumindo taxa de formação estelar constante e função inicial
de massa de Salpeter [Edwin Ernest Salpeter (1925-2008)]
(IMF ∝
M-2,35).
O tempo de vida na sequência principal está assumido como
tMS = 10-2,5 Ganos.
As curvas foram normalizadas no ponto indicado pelo círculo.
O pico em L/LSol~10-4 corresponde ao
acúmulo de anãs brancas devido à liberação de calor
por cristalização e acoplamento convectivo.
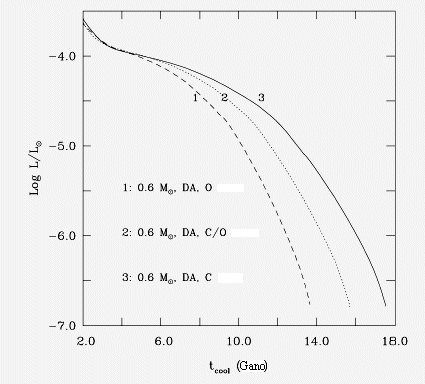 Curvas de esfriamento de tres modelos para uma anã branca de 0,6 MSol,
diferindo somente pela composição do núcleo. O modelo com núcleo
de C leva mais tempo para esfriar do que os outros modelos,
simplesmente por que tem mais partículas.
Curvas de esfriamento de tres modelos para uma anã branca de 0,6 MSol,
diferindo somente pela composição do núcleo. O modelo com núcleo
de C leva mais tempo para esfriar do que os outros modelos,
simplesmente por que tem mais partículas.
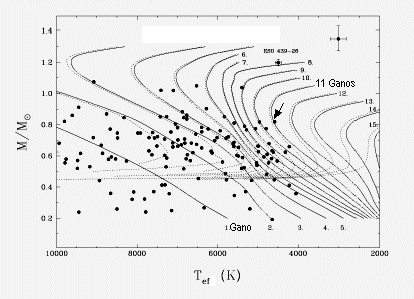
 Distribuição de 135 anãs brancas reportadas por
Pierre Bergeron, Sandy K. Legget e Maria Teresa Ruiz (2001, ApJS, 133, 415).
A barra de erros média está indicada no canto superior direito.
As curvas são isócronas, com idades expressas em Ganos. As
curvas sólidas representam somente o esfriamento das anãs brancas,
enquanto as linhas pontilhadas incluem a fase de evolução
na sequência principal, assumindo metalicidade solar. Os objetos com massa aparente abaixo
de 0,45 MSol representam mais provavelmente binárias
degeneradas não resolvidas,
mas também estrelas individuais
provenientes da fase de envelope comum de um sistema binário
interagente.
A teoria de evolução estelar não permite a formação de uma
anã branca com massa menor que 0,45 MSol no
tempo de Hubble. Para uma temperatura efetiva, uma binária
degenerada não resolvida interpretada como um objeto simples
será interpretada como um objeto com excesso de luminosidade,
ou seja, com raio maior e portanto massa menor, pela
relação massa-raio das estrelas degeneradas. As que forem realmente
individuais devem ter núcleo de hélio.
As duas estrelas mais velhas são as duas estrelas próximas
à isócrona de 11 Ganos.
Distribuição de 135 anãs brancas reportadas por
Pierre Bergeron, Sandy K. Legget e Maria Teresa Ruiz (2001, ApJS, 133, 415).
A barra de erros média está indicada no canto superior direito.
As curvas são isócronas, com idades expressas em Ganos. As
curvas sólidas representam somente o esfriamento das anãs brancas,
enquanto as linhas pontilhadas incluem a fase de evolução
na sequência principal, assumindo metalicidade solar. Os objetos com massa aparente abaixo
de 0,45 MSol representam mais provavelmente binárias
degeneradas não resolvidas,
mas também estrelas individuais
provenientes da fase de envelope comum de um sistema binário
interagente.
A teoria de evolução estelar não permite a formação de uma
anã branca com massa menor que 0,45 MSol no
tempo de Hubble. Para uma temperatura efetiva, uma binária
degenerada não resolvida interpretada como um objeto simples
será interpretada como um objeto com excesso de luminosidade,
ou seja, com raio maior e portanto massa menor, pela
relação massa-raio das estrelas degeneradas. As que forem realmente
individuais devem ter núcleo de hélio.
As duas estrelas mais velhas são as duas estrelas próximas
à isócrona de 11 Ganos.
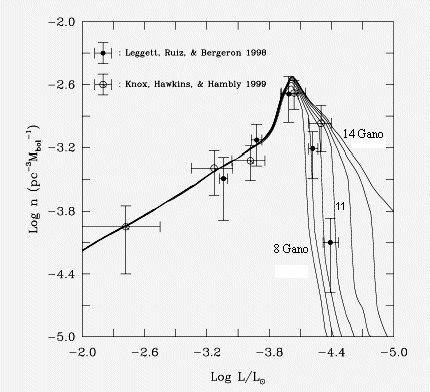 Comparação das funções luminosidades teóricas com o observada
por James W. Liebert,
Conard C. Dahn e David G. Monet (1988, Astrophysical Journal, 332, 891), mas recalibrada por
Sandy K. Legget,
Maria Teresa Ruiz e
Pierre Bergeron (1998, Astrophysical Journal, 497, 294)
e a observada por
R.A. Knox, M.R.S. Hawkins and Nigel C. Hambly (1999, Monthly Notices of the Royal Astronomical Society, 306, 736).
A melhor isócrona, incluindo o tempo de vida na sequência principal,
tem 11 Ganos para o disco local. Como os modelos têm núcleo de carbono, e metalicidade solar,
este é o limite superior para a idade.
Comparação das funções luminosidades teóricas com o observada
por James W. Liebert,
Conard C. Dahn e David G. Monet (1988, Astrophysical Journal, 332, 891), mas recalibrada por
Sandy K. Legget,
Maria Teresa Ruiz e
Pierre Bergeron (1998, Astrophysical Journal, 497, 294)
e a observada por
R.A. Knox, M.R.S. Hawkins and Nigel C. Hambly (1999, Monthly Notices of the Royal Astronomical Society, 306, 736).
A melhor isócrona, incluindo o tempo de vida na sequência principal,
tem 11 Ganos para o disco local. Como os modelos têm núcleo de carbono, e metalicidade solar,
este é o limite superior para a idade.
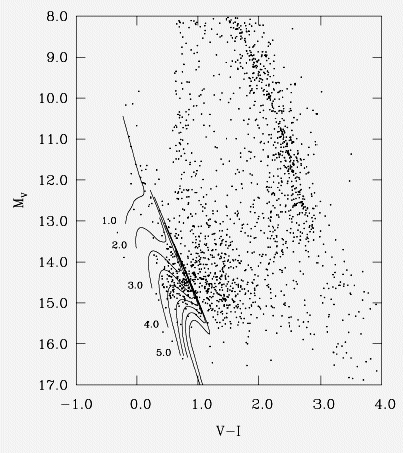
 Distribuição de 135 anãs brancas reportadas por
Pierre Bergeron, Sandy K. Legget e Maria Teresa Ruiz (2001, Astrophysical Journal Supplement Series, 133, 415)
no diagrama de magnitude absoluta × cor (V-I). As curvas
são isócronas, incluindo a evolução na sequência principal, para metalicidades solares,
com idades em Ganos, para modelos com 0,45 MSol (curva
superior) e 1,2 MSol (curva inferior). Note
que as cores (V-I) retornam para o azul para Tef <
4000K devido a formação de pseudo-moléculas de H2. Estas pseudo-moléculas
têm alta opacidade no infravermelho, forçando a radiação
para comprimentos de onda menores.
Distribuição de 135 anãs brancas reportadas por
Pierre Bergeron, Sandy K. Legget e Maria Teresa Ruiz (2001, Astrophysical Journal Supplement Series, 133, 415)
no diagrama de magnitude absoluta × cor (V-I). As curvas
são isócronas, incluindo a evolução na sequência principal, para metalicidades solares,
com idades em Ganos, para modelos com 0,45 MSol (curva
superior) e 1,2 MSol (curva inferior). Note
que as cores (V-I) retornam para o azul para Tef <
4000K devido a formação de pseudo-moléculas de H2. Estas pseudo-moléculas
têm alta opacidade no infravermelho, forçando a radiação
para comprimentos de onda menores.
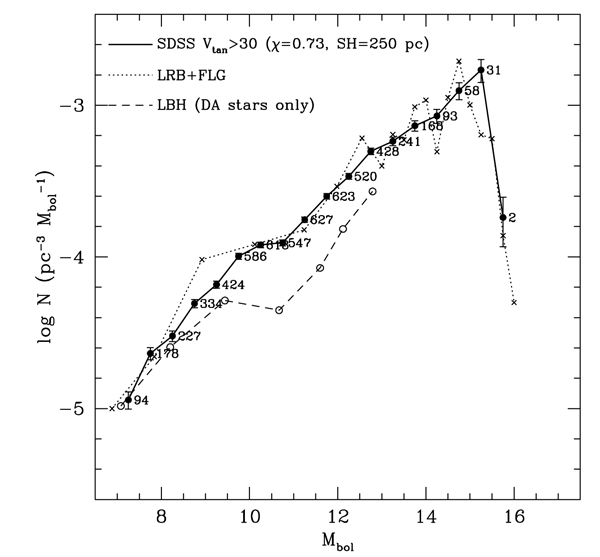
Função luminosidade obtida por Hugh C. Harris et al.
(2006, Astronomical Journal, 131, 571) com as anãs brancas,
do disco da Galáxia,
observadas pelo Sloan Digital Sky Survey, mas
selecionadas fotometricamente e não por espectroscopia.
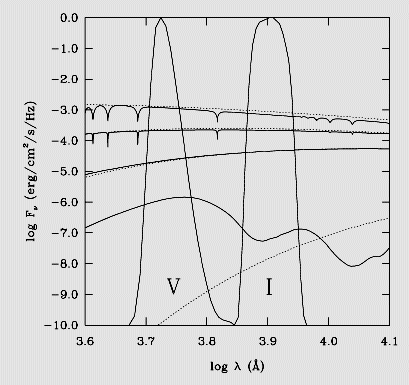
Evolução do fluxo emergente de uma anã branca de 0,6 MSol
para temperaturas efetivas de Tef=13 500 K,
7500 K, 4500 K e 1500 K (curvas sólidas de cima para baixo).
As distribuições de corpo negro correspondentes estão ilustradas
pelas linhas pontilhadas. As curvas de transmissão dos filtros V e
I também estão graficadas. Somente para a curva com menor temperatura,
Tef=1500 K vemos o excesso de fluxo abaixo de 10 000 Å.
Parte do diagrama cor-magnitude para o cúmulo aberto M67 observado
por Harvey B. Richer, Greg G. Falhman, J. Rosvick & R.A. Ibata
(1998, Astrophysical Jornal, 504, L91) com isócronas de 1 a 9 Ganos, incluindo o
tempo de vida dos progenitores na sequência principal, mas calculados para
metalicidade solar e não para a metalicidade do aglomerado.
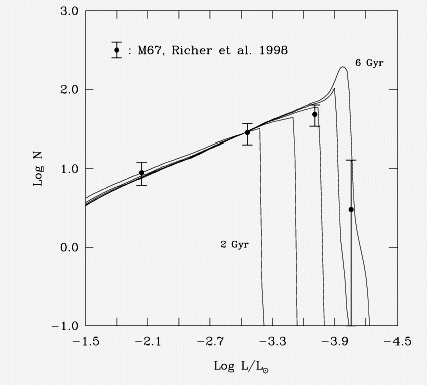
Comparação da função luminosidade com as isócronas para as anãs
brancas de M67.
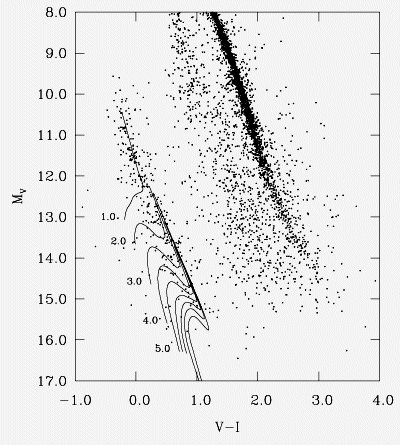
Parte do diagrama cor-magnitude para o cúmulo globular M4 observado
por Harvey B. Richer et al.
(1997, ApJ, 484, 741) com o Telescópio
Espacial Hubble. As isócronas graficadas são de 1 a 9 Ganos, incluindo o
tempo de vida dos progenitores na sequência principal.
O diagrama observado não se extende suficiente para mostrar as anãs
brancas mais velhas.
A observação de algumas anãs brancas próximas mas com alta velocidade,
além da observação de algumas anãs brancas no Hubble Deep Field
norte e sul, são compatíveis com um halo de 2 a 4 Ganos mais velho.
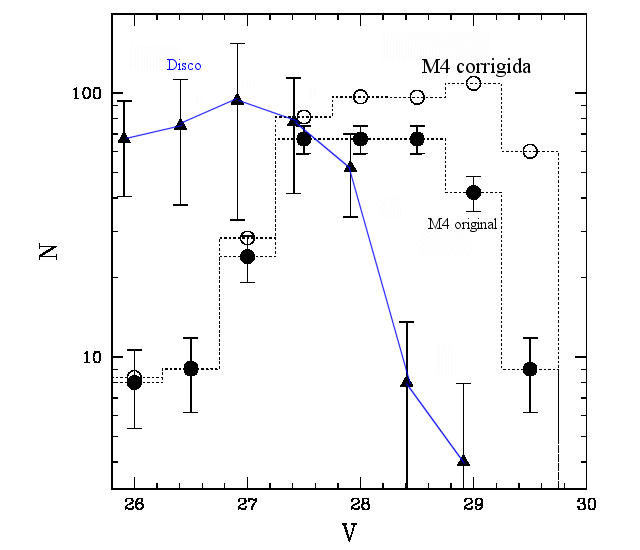
Distribuição de anãs brancas por magnitude aparente no cúmulo globular
M4, o mais próximo da Terra, a 7000 anos-luz de distância, obtida com
exposições totalizando 8 dias com a Wide Field Planetary Camera II do
Telescópio Espacial Hubble por Harvey Richer e colaboradores
(2002, Astrophysical Journal Letter, 574, L151).
A linha
azul mostra a curva equivalente para o disco galático, obtida por
Libert, Dahn e Monet em 1988. A nova distribuição,
publicada por Brad M.S. Hansen e colaboradores em 2002,
(Astrophysical Journal Letter, 574, L155)
apresenta anãs brancas ainda mais frias que no disco, levando a
uma idade entre 12 e 13 bilhões de anos para as anãs brancas e
13 a 14 bilhões de anos para o Universo.
O tempo de vida pré anã branca foi calculado para metalicidade solar, o que
exarceba a idade, já que os tempos de vida de estrelas de baixa metacilicade são muito
menores do que para metalicidade solar, chegando a um fator de 2× menor.
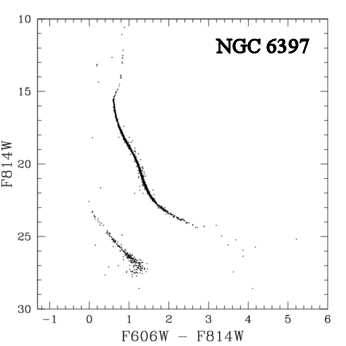 Diagrama HR do cúmulo globular NGC 6397, observado durante 126 órbitas com o Telescópio Espacial Hubble
e publicado por
Harvey B. Richer (UBC), Aaron Dotter (Dartmouth), Jarrod Hurley (Swinburne), Jay Anderson (Rice), Ivan King (Washington), Saul Davis (UBC), Gregory G. Fahlman (HIA/NRC), Brad M. S. Hansen (UCLA), Jason Kalirai (UCSC), Nathaniel Paust (STScI), R. Michael Rich (UCLA), Michael M. Shara (AMNH)
no Astronomical Journal, 135, 2141, em 2008, mostrando tanto a sequência principal
quanto a faixa de esfriamento das anãs brancas, até as anãs brancas mais frias, que se tornam azuis por
absorção devido a formação de pseudo-moléculas de H2
ou H-He, por colisões. As estrelas selecionadas para o diagrama têm
movimento próprio indetectável,
comparando com imagens obtidas vários anos antes com o
Wide Field Planetary Camera II e, portanto, não estão na frente do
cúmulo.
Diagrama HR do cúmulo globular NGC 6397, observado durante 126 órbitas com o Telescópio Espacial Hubble
e publicado por
Harvey B. Richer (UBC), Aaron Dotter (Dartmouth), Jarrod Hurley (Swinburne), Jay Anderson (Rice), Ivan King (Washington), Saul Davis (UBC), Gregory G. Fahlman (HIA/NRC), Brad M. S. Hansen (UCLA), Jason Kalirai (UCSC), Nathaniel Paust (STScI), R. Michael Rich (UCLA), Michael M. Shara (AMNH)
no Astronomical Journal, 135, 2141, em 2008, mostrando tanto a sequência principal
quanto a faixa de esfriamento das anãs brancas, até as anãs brancas mais frias, que se tornam azuis por
absorção devido a formação de pseudo-moléculas de H2
ou H-He, por colisões. As estrelas selecionadas para o diagrama têm
movimento próprio indetectável,
comparando com imagens obtidas vários anos antes com o
Wide Field Planetary Camera II e, portanto, não estão na frente do
cúmulo.
O desvio para o
azul (blue hook) das anãs brancas mais frias, causado pelas
absorções induzidas por colisões (CIA), primeiro observadas
em 1885 quando Pierre Jules
César Janssen (Comptes Rendus de l'Académie des sciences de Paris, 101, 649) observou que para o oxigênio a pressões
de centenas de atmosferas, novas bandas aparecerem e o coeficiente de absorção
passa de proporcional ao número de partículas do gás para proporcional ao
quadrado no número de partículas, isto é, indicando que as interações
ocorriam por pares de moléculas e não por moléculas individuais.
Em 1873, o físico holandês Johannes Diderik van der Waals (1837-1923) já havia postulado que as interações
intermoleculares incluíam uma componente atrativa, mas as absorções induzidas por colisão
causam linhas muito difusas devido à pequena duração da
colisão, da ordem de 10-13s, levando a uma largura natural muito grande pelo princípio
da incerteza de Heisenberg, enquanto as forças de van der Waals duram 10-10s ou mais.
Os momentos de dipolos induzidos pela interação causam um rearanjo temporário
das cargas eletrônicas, formando temporariamente uma supermolécula,
e produzindo absorções ou emissões além daquelas das moléculas não interagentes
[Collision-induced Absorption in Gases,
Lothar Frommhold, 1993, Cambridge University Press].
Neste caso, a pressão P precisa ser calculada como
onde V(r) é o potencial de interação, função da distância internuclear.
Pierre Bergeron
e Sandy K. Leggett, (2002, Astrophysical Journal, 580, 1070)
calcularam os espectros de anãs brancas frias incluindo os efeitos
de absorções induzidas por colisões de moléculas H2
com outras moléculas de H2,
calculados por
Aleksandra Borysow,
Uffe Gråe Jørgensen,
& Yi Fu (2001, Journal of
Quantum Spectra and Radiative Transfer, 68, 235),
mas também com He neutro, calculados por
Uffe Gråe Jørgensen,
Dominik Hammer,
Aleksandra Borysow
& Jens F. Falkesgaard (2000, Astronomy
& Astrophysics, 361, 283).
As absorções ocorrem por colisões de
H2-H2, H2-He e H-He.
Como
anãs brancas ricas em hélio frias tendem a ter opacidade menor e portanto
pressão atmosférica maior, a deficiência de fluxo infravermelho
aparece a temperaturas mais altas em anãs brancas ricas em hélio do
que nas ricas em hidrogênio.





Próxima: Campos magnéticos
Volta: Anãs Brancas
Anterior: Cristalização
©
Modificada em 6 out 2014
![]() , não há mais nenhuma anã branca observada.
O tempo de esfriamento das anãs brancas até estas
baixas luminosidades e temperaturas é maior do que a idade
do disco de nossa Galáxia, de modo que mesmo as
anãs brancas formadas na primeira geração de estrelas
ainda estão visíveis.
O halo é cerca de 2 bilhões de anos mais velho e as anãs brancas acima
de 0,8 massas solares já estão mais fracas que o limite de detecção
do Telescópio Espacial Hubble, mesmo para aquelas que estão nos
aglomerados globulares mais próximos.
, não há mais nenhuma anã branca observada.
O tempo de esfriamento das anãs brancas até estas
baixas luminosidades e temperaturas é maior do que a idade
do disco de nossa Galáxia, de modo que mesmo as
anãs brancas formadas na primeira geração de estrelas
ainda estão visíveis.
O halo é cerca de 2 bilhões de anos mais velho e as anãs brancas acima
de 0,8 massas solares já estão mais fracas que o limite de detecção
do Telescópio Espacial Hubble, mesmo para aquelas que estão nos
aglomerados globulares mais próximos.
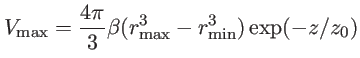
![]() luminosidade) --
foi primeiro explicado em 1987 por
Donald Earl Winget (1955-),
Carl John Hansen (1933-2011),
Hugh M. Van Horn (1938-),
Gilles Fontaine (1948-),
R. Edward Nather (1926-2014),
Kepler de Souza Oliveira Filho (1956-)
e Donald Quincy Lamb (1945-),
em termos da idade finita da
disco local da nossa Galáxia,
de cerca de 9 Ganos.
luminosidade) --
foi primeiro explicado em 1987 por
Donald Earl Winget (1955-),
Carl John Hansen (1933-2011),
Hugh M. Van Horn (1938-),
Gilles Fontaine (1948-),
R. Edward Nather (1926-2014),
Kepler de Souza Oliveira Filho (1956-)
e Donald Quincy Lamb (1945-),
em termos da idade finita da
disco local da nossa Galáxia,
de cerca de 9 Ganos.
![]() , em unidades de
, em unidades de
![]() ):
):
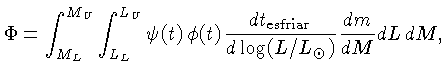



 Modelos de estrelas anãs brancas
de acordo com os cálculos de Gilles Fontaine (1948-), Pierre Brassard e
Pierre Bergeron, da Université de Montréal, no Canadá,
publicados
em 2001 no Publications of the Astronomical Society of the Pacific,
113, 409.
Modelos de estrelas anãs brancas
de acordo com os cálculos de Gilles Fontaine (1948-), Pierre Brassard e
Pierre Bergeron, da Université de Montréal, no Canadá,
publicados
em 2001 no Publications of the Astronomical Society of the Pacific,
113, 409.

















![$P = NkT - N^2 2\pi kT \int_0^\infty [\exp ( -\frac{V(r)}{kT})-1] r^2 dr$](pn2.png)