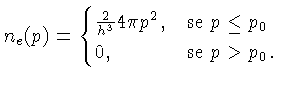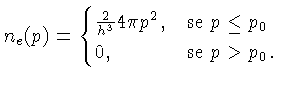Próxima: Degenerescência Total Não-Relativística
Volta: Degenerescência dos Elétrons
Anterior: Degenerescência dos Elétrons
Para altíssimas densidades (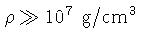 nos interiores
estelares), todos os níveis de energia até um valor máximo
estarão ocupados. Como a densidade total é finita, os
estados de densidade estarão ocupados até um certo valor
do momentum
nos interiores
estelares), todos os níveis de energia até um valor máximo
estarão ocupados. Como a densidade total é finita, os
estados de densidade estarão ocupados até um certo valor
do momentum 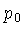 :
:
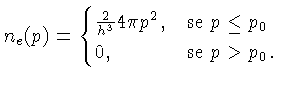 |
(1.10a) |
Naturalmente este é o estado de mínima energia cinética
para um gás de elétrons, pois todos os estados de energia mais
baixo estão ocupados, e nenhum de mais alta energia.
A densidade de partículas total é relacionada com o
momentum máximo por
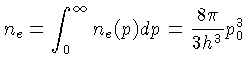 |
(1.11) |
ou escrevendo o momentum máximo em função da densidade
de elétrons:
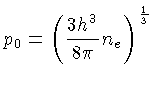 |
(1.12) |
A energia associada ao momentum máximo é a energia de Fermi.
Para expressar a velocidade da partícula em relação ao
seu momentum, precisamos distingüir entre um elétron
relativístico ou não-relativístico.





Próxima: Degenerescência Total Não-Relativística
Volta: Degenerescência dos Elétrons
Anterior: Degenerescência dos Elétrons
©
Modificada em 31 Maio 1999