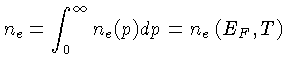Próxima: Degenerescência Total
Volta: Pressão Mecânica
Anterior: Gás de Fótons
O princípio da incerteza de Werner Karl Heisenberg (1901-1976),
acoplado ao princípio da exclusão de Wolfgang Pauli (1900-1958),
que diz que dois férmions não podem ocupar o mesmo estado quântico
simultaneamente, força os elétrons a altos níveis
de energia e, portanto, altas velocidades.
Matéria normal:
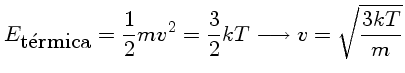
Matéria degenerada:
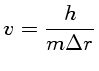
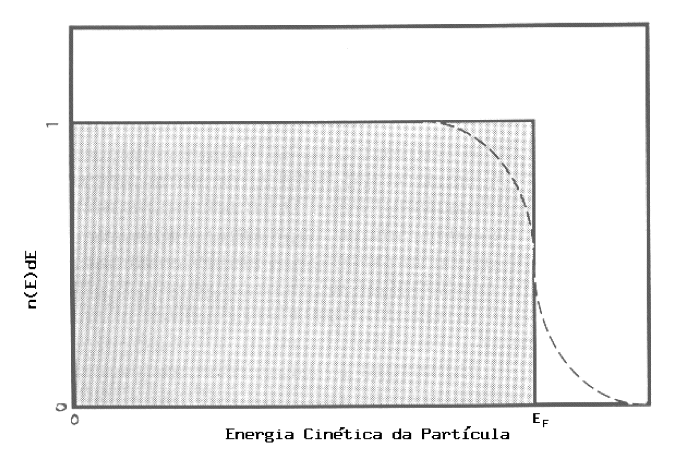 Distribuição de energia de
Fermi-Dirac para uma temperatura finita
(linha pontilhada), e para temperatura zero (linha contínua). Para
temperatura zero, equivalente a um gás totalmente degenerado, nenhuma
partícula tem energia superior à energia de Fermi (
Distribuição de energia de
Fermi-Dirac para uma temperatura finita
(linha pontilhada), e para temperatura zero (linha contínua). Para
temperatura zero, equivalente a um gás totalmente degenerado, nenhuma
partícula tem energia superior à energia de Fermi (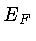 ).
).
Lembrando que a energia de Fermi é diretamente ligada ao
momentum devido ao princípio da incerteza, para um mesmo volume
todos os férmions terão o mesmo momentum.
Como a energia associada a este momentum p é dada por
E=p2/2m, no caso não relativístico,
onde m é a massa da partícula, os prótons
e nêutrons, por terem massa cerca de 2000 vezes maior do que
a dos elétrons, têm energia de Fermi 2000 vezes menor e,
portanto, precisam estar em um volume 2000 vezes menor que para
os elétrons, para estarem
degenerados.
No interior dos planetas gigantes e estrelas evoluídas,
os elétrons estão degenerados, mas os prótons
e nêutrons não. Nas estrelas de nêutrons, com
raio cerca de 1000 vezes menor que o das anãs brancas,
os nêutrons estão degenerados, e as derivações
a seguir se aplicam, substituindo-se elétrons por nêutrons.
Como os elétrons são partículas de spin semi-inteiro,
um gás de elétrons obedece a estatística de Fermi-Dirac.
A densidade de elétrons com momentum
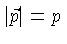 no
intervalo
no
intervalo 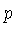 e
e 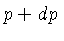 é dada pela equação (1.2):
é dada pela equação (1.2):
onde definimos o índice de ocupação para um gás de Fermi como
O fato de 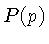 ter valor máximo de um é uma expressão do
princípio de exclusão de Pauli. Quando
ter valor máximo de um é uma expressão do
princípio de exclusão de Pauli. Quando 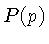 é unitário,
todos os níveis de energia do gás estão ocupados. Portanto,
a máxima densidade de elétrons, no espaço de fase, é
é unitário,
todos os níveis de energia do gás estão ocupados. Portanto,
a máxima densidade de elétrons, no espaço de fase, é
![[n_e(p)]_{max} = \frac{2}{h^3}4\pi p^2 dp](img88.gif) |
(1.10) |
É esta restrição na densidade de elétrons no espaço
de momentum que cria a pressão de degenerescência. Se aumentamos
continuamente a densidade de elétrons,
os elétrons são forçados
a um estado de maior momentum e, portanto, maior pressão, simplesmente
porque todos estados de momentum mais baixo já estão ocupados.
Para qualquer temperatura e densidade de elétrons 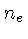 ,
o valor da Energia de Fermi (
,
o valor da Energia de Fermi (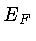 ) é determinado pela integral
) é determinado pela integral
Se 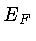 for um número grande e negativo,
for um número grande e negativo, 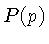 será menor do que um para todas as energias, e a distribuição
de Fermi-Dirac se reduz a uma distribuição Maxwelliana.
Conforme a densidade for aumentando, para uma temperatura constante,
a energia de Fermi se torna primeiro pequena,
cruzando zero e chegando a grandes valores
positivos, em altas densidades. Se a energia de Fermi
for muito maior do que
será menor do que um para todas as energias, e a distribuição
de Fermi-Dirac se reduz a uma distribuição Maxwelliana.
Conforme a densidade for aumentando, para uma temperatura constante,
a energia de Fermi se torna primeiro pequena,
cruzando zero e chegando a grandes valores
positivos, em altas densidades. Se a energia de Fermi
for muito maior do que 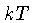 , a distribuição
será uma função degrau, e chamamos este limite de
degenerescência total.
, a distribuição
será uma função degrau, e chamamos este limite de
degenerescência total.





Próxima: Degenerescência Total
Volta: Pressão Mecânica
Anterior: Gás de Fótons
 Astronomia e Astrofísica
Astronomia e Astrofísica

©
Modificada em 23 mar 2009
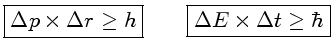
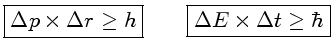
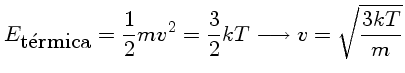
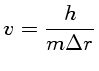

![]() no
intervalo
no
intervalo ![]() e
e ![]() é dada pela equação (1.2):
é dada pela equação (1.2):
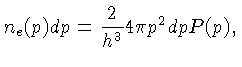
![P(p)=[\exp(\frac{E-E_F}{kT})+1]^{-1}](img86.gif)
![]() ,
o valor da Energia de Fermi (
,
o valor da Energia de Fermi (![]() ) é determinado pela integral
) é determinado pela integral