Cancelamento Geométrico

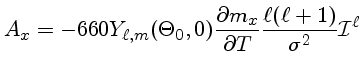
A fórmula para a amplitude de uma pulsação modo-g, em uma anã branca DAV, obtida em Robinson, Kepler & Nather (1982), é:

$A_x=-660 Y_{\ell,m}(\Theta_0,0) \frac{\partial m_x}{\partial T} \frac {\ell(\ell+1)}{\sigma^2} \cal{I}^\ell$

onde $\sigma$ é a freqüência de pulsação:

$\delta \zeta = \zeta_0 K_{\ell,m}(r)Y_{\ell,m}(\theta,\phi)e^{i\sigma t}$

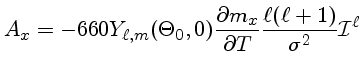
$\ell$	$\cal{I}^\ell$	Cancelamento
0	5/6	0,833
1	7/12	0,583
2	31/120	0,258
3	1/24	0,042
4	-1/48	-0,021

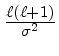de modo que cancelamento ($\ell=1$)/cancelamento ($\ell=2$)=2,258. O termo $\frac{\ell(\ell+1)}{\sigma^2}$ é constante com $\ell$, pois este termo vem diretamente da condição de contorno na superfície, $\delta r/r=1$ proposto por Yoji Osaki & Carl Hansen, no artigo Nonradial Oscillations of Cooling White Dwarfs, publicado em 1973 no Astrophysical Journal, 185, 273.

Note que embora para uma DAV a deslocamento radial de uma pulsação seja somente da ordem de um metro, o termo $\delta r/r=1$ garante que a pulsação cubra a superfície da estrela e, por isso, o termo $\ell(\ell+1)/\sigma^2$ é constante com $\ell$, pois corresponde ao número inteiro de comprimentos de onda em $2\pi r$.

Mode Trapping

O mecanismo de filtro que seleciona que modos são excitados para amplitudes observáveis, dentro todos os autovalores possíveis, mode trapping, foi estudado por Don Earl Winget, Hugh M. van Horn & Carl J. Hansen (1981, Astrophysical Journal, 245, L33) e Alejandro Hugo Córsico, Leandro G. Althaus, Omar G. Benvenuto, & Aldo M. Serenelli (2002, Astronomy & Astrophysics, 387, 531).

Das observações, vemos que para as pré-anãs brancas DOVs, com $T_{eff}\simeq 170 000$ K a 75000K e $\log g=5.7$ a 7.5, têm centenas de modos excitados, as anãs brancas DBVs, com $T_{eff}\simeq 22 000$K a 29000K têm dezenas de modos excitados, e as DAVs, com $T_{eff}\simeq 10 850$K a 12270K têm poucos modos excitados.

Nas pré-anãs brancas, as camadas superiores ainda são de composição química homogênea, pois estas estrelas recém saíram do Ramo Assintótico das Supergigantes, com extensas camadas de convecção. As zonas de transição de composição química ocorrem principalmente entre o núcleo de C/O e as camadas mais externas. É interessante notar que mesmo a estrela quente PG 1159-035, entretanto, já apresenta mode trapping, como detectado por José Eduardo da Silveira Costa em sua tese de doutorado (Costa et al. 2006). Como a estrela é bem quente, a energia disponível para pulsação é alta, e os modos de pulsação detectados têm $k\simeq 30$-50. Como as zonas de transição são ainda bastante inclinadas, já que a difusão gravitacional ainda está no início ($\tau_{dif}\simeq 10^6 - 10^8$ anos), centenas de modos de pulsação têm comprimentos de onda efetivos similares às cavidades equivalentes descritas pelas zonas de transição. Por isto muitos modos são observados.

Para as DBVs, as camadas de transição já têm gradientes mais fortes, pois a difusão ainda está em curso mas já passou por várias escalas de tempo de difusão, e já separaram as camadas de He razoavelmente, levando os elementos mais pesados para o interior. Como as pulsações têm $k\simeq 10$-20 face à temperatura mais baixa, somente dezenas de modos de pulsação têm comprimentos de onda efetivos similares às cavidades equivalentes descritas pelas zonas de transição.

Já para as DAVs, a energia disponível para pulsação é baixa face à reduzida energia térmica disponível nas camadas externas, e somente os modos com $k\leq 6$ são excitados e, portanto, os comprimentos de onda efetivos são longos. Como a difusão já separou completamente as camadas de composição química diferentes, existem pelo menos três zonas de transição: C/O, He e H, que amarram os modos de pulsação. Estas transições abruptas também explicam o fenômeno de cruzamentos proibidos (avoided crossings), pois os modos não conseguem ultrapassar as barreiras das transições até que suas energias sejam altas o suficientes, e aí já têm energia suficiente para chegar até a outra barreira, com períodos similares aos daquele que correspondem a esta outra cavidade.

Volta: Pulsações
Volta: Evolução Estelar
Volta: Astronomia e Astrofisica