| Pulsações Não-Radiais | Não Adiabáticas | Heliosismologia | Anãs Brancas | ZZ Cetis | Wu |
Estrelas variáveis são aquelas em que a variação não representa apenas as flutuações normais de grandes conjuntos de partículas em movimentos turbulentos, mas apresentam amplitudes mensuráveis com um certo grau de regularidade [Paul Ledoux (1914-1988) & Théodore Walraven (1916-2008), 1958].
No livro Asteroseismology, de Conny Aerts, Jørgen Christensen-Dalsgaard e Donald W. Kurtz, 2010, Springer, podemos ler que numa orquestra, mesmo tocando a mesma nota, podemos distinguir cada instrumento porque a forma e material do instrumento determina quanta potência é colocada em cada um de seus harmônicos naturais. A combinação de frequências, amplitudes e fases de cada harmônico define o timbre do instrumento.



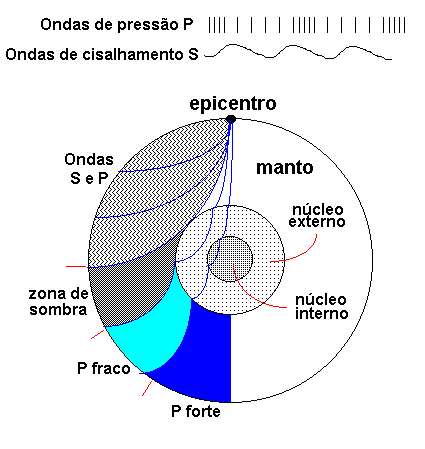
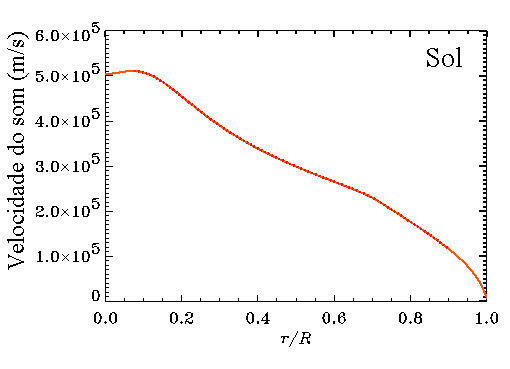
O som é uma onda de pressão. A compressão e rareficação do gás propaga esta onda. Em um gás ideal, as mudanças de pressão são acompanhadas por mudanças na densidade e na temperatura. Se a temperatura é maior, as moléculas estão se movendo mais rápido, colidem mais frequentemente, e a velocidade do som é maior. E para uma mesma temperatura, gases leves se movem mais rápido e, portanto, a velocidade do som é maior para gases mais leves. Desta maneira, se medimos a velocidade do som nas estrelas, podemos determinar a densidade e, através da equação de estado, podemos estudar a temperatura e a composição.
Na Terra, as ondas de pressão, primárias, têm velocidade de 6 km/s na terra e nas rochas, mas somente 1/3 disto na água. As ondas "s", de cisalhamento, secundárias, têm velocidade de 3 km/s, mas maior amplitude e, portanto, maior poder de destruição.

A estrutura de uma estrela é fundamentalmente determinada pela
mecânica. Relembramos que o tempo dinâmico, ou tempo de queda livre,
(![]() ) é normalmente pequeno
se comparado com o tempo de variação da energia dentro da
estrela, por exemplo o tempo de Kelvin-Helmoltz
(
) é normalmente pequeno
se comparado com o tempo de variação da energia dentro da
estrela, por exemplo o tempo de Kelvin-Helmoltz
(![]() ).
Isto não é estritamente válido para todas estrelas, ou mesmo
para as partes externas da maioria das estrelas,
mas forma a base da aproximação adiabática
no estudo das pulsações estelares. Nesta aproximação, assumimos
que todos os mecanismos de mudança de energia podem ser ignorados,
de modo que o sistema é puramente mecânico.
Por exemplo, o som de um sino depende muito mais de sua estrutura
do que da energia dada por uma batida.
O problema, nesta aproximação, se reduz a estudar os modos normais
de um sistema equivalente a pêndulos e molas, ou mais corretamente,
ao estudo de ondas sonoras em uma caixa.
A aproximação adiabática é extremamente útil na teoria de estrelas
variáveis porque simplifica a análise, e produz resultados
precisos da resposta dinâmica da maioria das estrelas. O preço
pago é severo, entretanto, porque não nos diz nada sobre a causa
real da pulsação das estrelas. Em geral, a pulsação ocorre como uma
forma de transporte de energia, com uma equipartição de energia por
todos os caminhos possíveis, inversamente proporcional à
resistência do material, similar à resistência paralela.
).
Isto não é estritamente válido para todas estrelas, ou mesmo
para as partes externas da maioria das estrelas,
mas forma a base da aproximação adiabática
no estudo das pulsações estelares. Nesta aproximação, assumimos
que todos os mecanismos de mudança de energia podem ser ignorados,
de modo que o sistema é puramente mecânico.
Por exemplo, o som de um sino depende muito mais de sua estrutura
do que da energia dada por uma batida.
O problema, nesta aproximação, se reduz a estudar os modos normais
de um sistema equivalente a pêndulos e molas, ou mais corretamente,
ao estudo de ondas sonoras em uma caixa.
A aproximação adiabática é extremamente útil na teoria de estrelas
variáveis porque simplifica a análise, e produz resultados
precisos da resposta dinâmica da maioria das estrelas. O preço
pago é severo, entretanto, porque não nos diz nada sobre a causa
real da pulsação das estrelas. Em geral, a pulsação ocorre como uma
forma de transporte de energia, com uma equipartição de energia por
todos os caminhos possíveis, inversamente proporcional à
resistência do material, similar à resistência paralela.
Nesta seção trataremos dos movimentos radiais. Desta maneira assumimos que a estrela mantém a simetria esférica e podemos desprezar os efeitos de rotação, campo magnético, etc.
Como a transferência de calor é ignorada na aproximação adiabática, podemos descrever a estrutura mecânica somente com as equações de massa e de força
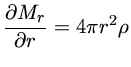 |
(1) |
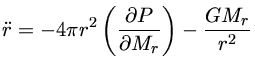 |
(2) |
| (3) |
| (4) |
Podemos agora linearizar as equações de força e de massa substituindo
a posição (raio) e densidade deste elemento de massa pelos
valores perturbados
(3) e (4) e, no resultado, mantendo somente os
termos de primeira ordem em
![]() e
e
![]() .
Consideremos a equação de massa
.
Consideremos a equação de massa
![$ {\partial M_r\over \partial[r_0(1+\delta r/r_0)]}= 4\pi[r_0(1+\delta r/r_0)]^2[\rho_0 (1+\delta\rho/\rho_0)].$](img17.gif) |
(5) |
![$ {{\partial M_r \over \partial r_0 }}[1-{\delta r\over r_0}
-r_0{{\partial (\delta r/r_0) \over \partial r_0 }}].
$](img21.gif)
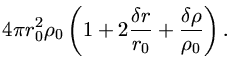
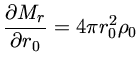
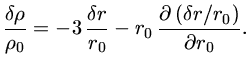 |
(6) |
Relações homólogas são definidas como
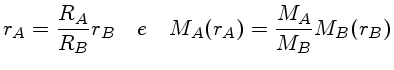
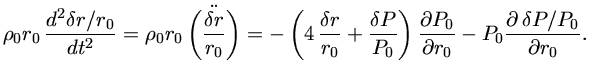 |
(7) |
Neste ponto da análise tomamos o caminho tradicional em teoria de
perturbação e assumimos que todos as perturbações prefixadas por
![]() pode ser decompostas nas componentes de Fourier com
o elemento de tempo representado por exponenciais.
Desta maneira, introduzimos a componente espacial do deslocamento
relativo do fluido,
pode ser decompostas nas componentes de Fourier com
o elemento de tempo representado por exponenciais.
Desta maneira, introduzimos a componente espacial do deslocamento
relativo do fluido,
![]() , como
, como
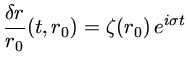 |
(8) |

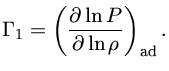 |
(9) |
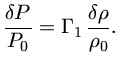 |
(10) |
Dentre os vários caminhos que podemos tomar, escolhemos o seguinte:
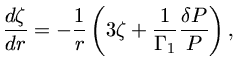 |
(11) |
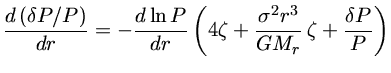 |
(12) |
Obtemos portanto um conjunto de equações diferenciais de primeira ordem
acopladas, mas precisamos de condições de contorno.
A primeira é simples porque exigimos que
![]() seja zero no centro (
seja zero no centro (![]() ).
Para ver como isto ocorre, considere uma partícula de extensão
infinitesimal exatamente no centro de equilíbrio da estrela. Não
existe qualquer lugar que a partícula possa se mover
(
).
Para ver como isto ocorre, considere uma partícula de extensão
infinitesimal exatamente no centro de equilíbrio da estrela. Não
existe qualquer lugar que a partícula possa se mover
(![]() ) sem violar a condição de simetria radial.
A regularidade física também requer que
) sem violar a condição de simetria radial.
A regularidade física também requer que
![]() e
e ![]() sejam finitos no centro.
A única maneira disto ser verdadeiro é se o termo em parêntesis
no lado direito da equação (11) se anular no centro. Isto produz
a segunda condição de contorno
sejam finitos no centro.
A única maneira disto ser verdadeiro é se o termo em parêntesis
no lado direito da equação (11) se anular no centro. Isto produz
a segunda condição de contorno
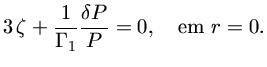 |
(13) |

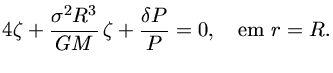 |
(14) |
Agora temos um número igual de equações diferenciais e de condições
de contorno. Mas todas as equações que derivamos são lineares
e homogêneas em
![]() e
e
![]() de modo que permanece a questão sobre
como estas quantidades são linearizadas. Como estão, qualquer
rescalonamento é permitido, para qualquer das duas perturbações,
em um ponto qualquer da estrela, e a solução pode ser tão grande
ou tão pequena quanto queiramos. Para restringir, precisamos
escolher uma normalização não nula. Isto é completamente arbitrário,
mas escolhemos
de modo que permanece a questão sobre
como estas quantidades são linearizadas. Como estão, qualquer
rescalonamento é permitido, para qualquer das duas perturbações,
em um ponto qualquer da estrela, e a solução pode ser tão grande
ou tão pequena quanto queiramos. Para restringir, precisamos
escolher uma normalização não nula. Isto é completamente arbitrário,
mas escolhemos
 |
(15) |
![$ {\bf L}(\zeta)\equiv-{1\over\rho r^4} {d \over dr}({\Gamma_...
...\over dr} [(3{\Gamma_1}-4)P]\}\zeta=\sigma^2\zeta$](img55.gif) |
(16) |
Todas as quantidades em
![]() são bem comportadas e
são bem comportadas e
![]() é um operador de Sturm-Liouville
[Jacques Charles François Sturm (1803-1855),
Mémoire sur la résolution des équations numériques, 1829;
Joseph Liouville (1809-1882)], que permite a expansão das funções
em séries.
Podemos também simbolicamente integrar sobre toda a estrela e mostrar
que
é um operador de Sturm-Liouville
[Jacques Charles François Sturm (1803-1855),
Mémoire sur la résolution des équations numériques, 1829;
Joseph Liouville (1809-1882)], que permite a expansão das funções
em séries.
Podemos também simbolicamente integrar sobre toda a estrela e mostrar
que
 |
(17) |
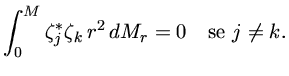 |
(18) |
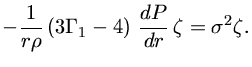 |
(19) |
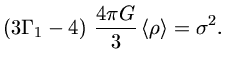 |
(20) |
 |
(21) |
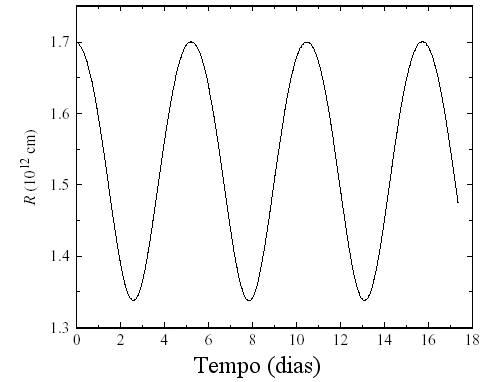
A estrela V725 Sgr tinha um período de 12 dias em 1926, mas seu período atualmente é de cerca de 90 dias, estando possivelmente em um pulso térmico no Ramo Gigante Assintótico (John R. Percy, Anna Molak, Hugh Lund, M. Danie Overbek, Amelia Wehalau e Peter F. Williams, 2006, JAAVSO, 34, 276).
Para uma
anã branca não relativística,
![]() . Como a densidade é, por definição,
. Como a densidade é, por definição,
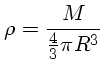

Se,
![]() sabemos que encontraremos problemas,
pois neste caso a energia total é menor que a energia de ligação.
Neste caso
sabemos que encontraremos problemas,
pois neste caso a energia total é menor que a energia de ligação.
Neste caso
![]() é imaginário e o tempo de crescimento por um fator de e
para o crescimento e decaimento dos movimentos é
é imaginário e o tempo de crescimento por um fator de e
para o crescimento e decaimento dos movimentos é
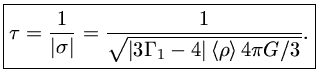 |
(22) |

| Classe | Tipo | Período | Tef (K) | log L/LSol |
|---|---|---|---|---|
| Sol e tipo solar | p | 3m a horas | 4500 a 6600 | -0,5 a 2,0 |
| γ Dor | g | 8h a 5d | 6800 a 8000 | 0,7 a 1,1 |
| δ Scuti e SX Phe (Pop II) | p | 15m a 8h | 6600 a 9000 | 0,6 a 2,0 |
| roAp | p | 5 a 22m | 6800 a 8500 | 0,8 a 1,5 |
| RR Lyrae | F,F+1 | 0,3 a 0,5d | 6000 a 7600 | 1,4 a 1,7 |
| Cefeidas, W Vir | F | 1 a 30d | 5000 a 7900 | 2,0 a 4,0 |
| Mira | l=0 | >80d | 2800 a 5600 | 2,4 a 4,0 |
| WR | g,S | 1h a 5d | 25000 a 50000 | 4,5 a 6,0 |
| β Cephei | p e g | 1 a 12h | 18000 a 30000 | 2,0 a 5,0 |
| sdB | p e g | 80 a 800s; 0,5 a 3h | 16000 a 40000 | 1,2 a 2,6 |
| DOV, GW Vir, PG1159 | g | 5 a 80m | 65000 a 140000 | 1,5 a 3,5 |
| DBV, V777 Her | g | 2 a 16m | 20000 a 30000 | -1,0 a 0,7 |
| DAV, ZZ Ceti | g | 71 a 4000s | 9000 a 12500 | -2,8 a -2,2 |
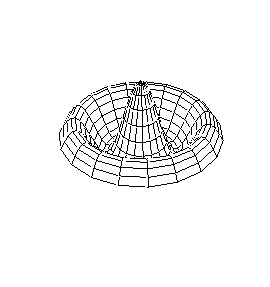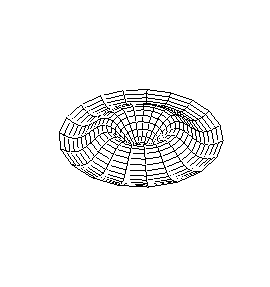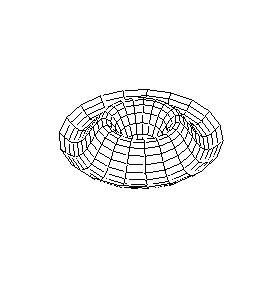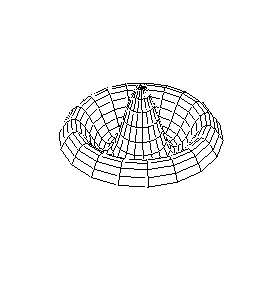 Em duas dimensões, podemos visualizar as oscilações da membrana de um tambor.
Existem nodos em duas direções ortogonais. Um conjunto de modos são
círculos concêntricos, e são chamados de modos radiais.
Como a membrana
está presa na borda do tambor, a borda é sempre um nodo. O modo radial
fundamental move a membrana para cima e para baixo, mantendo a simetria
radial e com amplitude máxima no centro. O primeiro sobretom radial
tem um nodo que é um círculo concêntrico, com os ânulo externo movendo-se
em antifase ao círculo central.
Em duas dimensões, podemos visualizar as oscilações da membrana de um tambor.
Existem nodos em duas direções ortogonais. Um conjunto de modos são
círculos concêntricos, e são chamados de modos radiais.
Como a membrana
está presa na borda do tambor, a borda é sempre um nodo. O modo radial
fundamental move a membrana para cima e para baixo, mantendo a simetria
radial e com amplitude máxima no centro. O primeiro sobretom radial
tem um nodo que é um círculo concêntrico, com os ânulo externo movendo-se
em antifase ao círculo central.
 Dan Russel produziu
animações de oscilações uni e bidimensionais.
Dan Russel produziu
animações de oscilações uni e bidimensionais.
A segunda direção de nodos em um tambor dá origem aos modos não radiais. O primeiro modo é um dipolo, que tem um nodo em uma linha dividindo a membrana em duas, com as duas metades oscilando em antifase. O segundo modo tem duas linhas nodais, dividindo a membrana em quatro partes. Como as frequências dos modos não são múltiplos inteiros, estes modos não são harmônicos. Se a densidade e tensão da membrana forem uniformes, as soluções das equações de onda são funções de Bessel.
As estrelas são tridimensionais e suas oscilações naturais têm nodos em três direções ortogonais, normalmente descritos pela distância r ao centro, a latitude θ e a longitude Φ. Os nodos são camadas concêntricas de r constante, cones de θ constante e planos de Φ constante. Na maioria das estrelas o eixo de pulsação coincide com o eixo de rotação, mas existem estrelas com modos de pulsação alinhados com o eixo magnético, como no caso das estrelas Ap rapidamente oscilantes. A analogia da pulsação das estrelas com um instrumento musical para o primeiro modo radial, em que a estrela se expande e se contrai - esfria e esquenta, pode ser feita com um tubo de órgão, já que há um nodo no núcleo, que não se move, e um antinodo (região de maior amplitude) na superfície. Os períodos dos sobretons não são múltiplos inteiros, porque há um gradiente na velocidade do som no interior da estrela, causado pelo gradiente de temperatura e de composição em algumas camadas. O primeiro modo não radial é um dipolo simétrico em relação ao eixo de pulsação: o hemisfério norte se expande e o hemisfério sul se contrai, e vice-versa.

Não descreveremos, por enquanto, as perdas e ganhos de energia, que são necessárias para determinar a estabilidade de um dado modo. Esta aproximação é chamada aproximação adiabática e é útil na determinação dos períodos de pulsação, que dependem essencialmente da estrutura mecânica da estrela.
As referências principais para a teoria de oscilações não radiais são:
As equações que descrevem o comportamento dinâmico do fluido são: a equação de Poisson para o potencial gravitacional, a equação da continuidade e a equação de movimento.
| (23) |
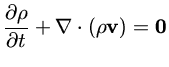 |
(24) |
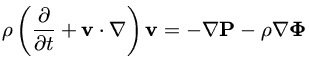 |
(25) |
Assumimos que conhecemos o valor das variáveis físicas da estrela não
perturbada em função de
![]() .
Imaginamos que cada elemento de fluido na estrela seja
deslocado de sua posição de equilíbrio em
.
Imaginamos que cada elemento de fluido na estrela seja
deslocado de sua posição de equilíbrio em
![]() por uma distância vetorial arbitrária e infinitesimal,
por uma distância vetorial arbitrária e infinitesimal,
![]() .
Este tipo de deslocamento - que toma um elemento de fluido identificável
e o move a outro lugar
- é um deslocamento Lagrangiano, que denotamos por
.
Este tipo de deslocamento - que toma um elemento de fluido identificável
e o move a outro lugar
- é um deslocamento Lagrangiano, que denotamos por
![]() .
Quando
.
Quando ![]() em um modelo em equilíbrio,
as perturbações Eulerianas e Lagrangianas
de
em um modelo em equilíbrio,
as perturbações Eulerianas e Lagrangianas
de ![]() , descritas respectivamente por
, descritas respectivamente por ![]() e
e
![]() ,
são as mesmas e são dadas por:
,
são as mesmas e são dadas por:
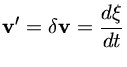 |
(26) |
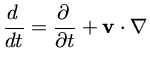 |
(27) |
Se o movimento é adiabático, a relação entre
![]() e
e
![]() é a mesma que no caso radial:
é a mesma que no caso radial:
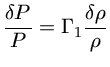 |
(28) |
| (29) |
Agora vamos substituir ![]() ,
,
![]() ,
,
![]() e
e ![]() , por
, por
![]() ,
,
![]() ,
,
![]() e
e ![]() nas equações anteriores,
multipicando todos os termos, e mantendo somente os termos de primeira ordem.
Como um exemplo, a equação de força torna-se:
nas equações anteriores,
multipicando todos os termos, e mantendo somente os termos de primeira ordem.
Como um exemplo, a equação de força torna-se:
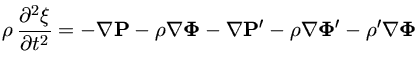 |
(30) |
| (31) |
| (32) |
| (33) |
Embora tenhamos linearizado as equações, o conjunto de equações
diferenciais parciais que obtivemos é de segunda ordem no tempo e
de quarta ordem no espaço.
Com o objetivo de reduzir as equações diferenciais parciais em
equações diferenciais ordinárias,
assumimos que as pulsações são periódicas e podem ser
analisadas por séries de Fourier.
Esta hipótese permite assumir que todas as variáveis têm uma dependência
temporal proporcional a
![]() , onde
, onde
![]() é a frequência angular.
Por examplo, assumimos para
é a frequência angular.
Por examplo, assumimos para
![]() :
:
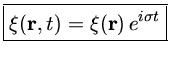 |
(34) |
Como a energética das oscilações não radiais indica que a amplitude radial
é pequena, podemos modelar a porção angular das pulsações através de
esféricos harmônicos. Desta forma, a solução para
![]() e
e
![]() é:
é:
![$ [\xi_r(r)\,\pmb{{\bf\rm e}_r}+\xi_t(r)\,
\pmb{{\bf\rm e}_\th...
...in{\theta}}{\partial\ \over\partial\varphi}]
\,Y_{\ell m}(\theta,\varphi)$](img125d.gif) |
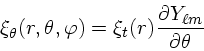
 No livro de John David Jackson (1925-)
[1975, Classical Electrodynamics, 2nd ed., (New York:Wiley & Sons)]
e no livro de Eugene Merzbacher,
[1970, Quantum Mechanics, 2nd ed., (New York: Wiley & Sons)]
existe uma discussão compacta de esféricos harmônicos.
Como a base de esféricos harmônicos é completa, podemos representar qualquer
distribuição angular por uma soma de esféricos harmônicos, mas o que queremos
aqui é atribuir um único
No livro de John David Jackson (1925-)
[1975, Classical Electrodynamics, 2nd ed., (New York:Wiley & Sons)]
e no livro de Eugene Merzbacher,
[1970, Quantum Mechanics, 2nd ed., (New York: Wiley & Sons)]
existe uma discussão compacta de esféricos harmônicos.
Como a base de esféricos harmônicos é completa, podemos representar qualquer
distribuição angular por uma soma de esféricos harmônicos, mas o que queremos
aqui é atribuir um único
![]() e
e ![]() a cada modo de pulsação.
Isto é possível no caso de rotação lenta,
mas não é válido para o caso de rotação rápida ou da existência de
campos magnéticos fortes.
O índice
a cada modo de pulsação.
Isto é possível no caso de rotação lenta,
mas não é válido para o caso de rotação rápida ou da existência de
campos magnéticos fortes.
O índice
![]() é chamado de grau harmômico, m é chamado
de número azimutal e n, o número de nodos entre o centro
e a superfície da estrela, de ordem radial.
é chamado de grau harmômico, m é chamado
de número azimutal e n, o número de nodos entre o centro
e a superfície da estrela, de ordem radial.
As funções esféricos harmônicos
![]() são dadas por
são dadas por
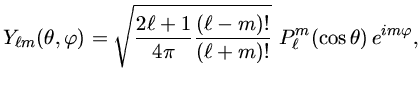
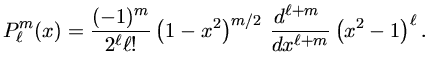
Antes de continuar, definimos algumas frequências importantes. A
primeira é a frequência de
Brunt-Väisälä
![]() :
:
![$ {N^2=-Ag=-g[{d\ln{\rho}\over dr}-{1\over\Gamma_1 }{d\ln{P}\over dr} ] }$](img137.gif) |
(35) |
A segunda frequência é a frequência de Lamb, ![]() , definida em 1910 pelo
matemático inglês Sir Horace Lamb (1849-1934), como:
, definida em 1910 pelo
matemático inglês Sir Horace Lamb (1849-1934), como:
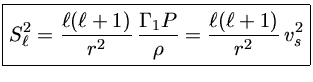 |
(36) |
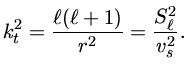
Em 1940, Carl-Gustaf Rossby (1898-1957) mostrou que os gradientes horizontais
do potencial de vorticidade
(![]() )
podem atuar como uma força restauradora para
perturbações ondulatórias, atualmente chamadas de ondas de
Rossby, ou modos-r.
No Sol, as ondas de Rossby na fotosfera têm amplitude radial de
cerca de 100 metros e deslocamentos horizontais de
45000 km, e já foram medidas pelo satélite SOHO.
Na atmosfera da Terra, os deslocamentos radiais são da ordem de
5 cm e os horizontais de cerca de 500 km.
)
podem atuar como uma força restauradora para
perturbações ondulatórias, atualmente chamadas de ondas de
Rossby, ou modos-r.
No Sol, as ondas de Rossby na fotosfera têm amplitude radial de
cerca de 100 metros e deslocamentos horizontais de
45000 km, e já foram medidas pelo satélite SOHO.
Na atmosfera da Terra, os deslocamentos radiais são da ordem de
5 cm e os horizontais de cerca de 500 km.
Podemos aprender bastante das soluções da equação diferencial ordinária
para ![]() e
e ![]() realizando uma análise local do sistema.
Assumimos que
realizando uma análise local do sistema.
Assumimos que ![]() e
e
![]() têm variações espaciais mais rápidas do que as
outras variáveis físicas que aparecem nas equações
(por exemplo
têm variações espaciais mais rápidas do que as
outras variáveis físicas que aparecem nas equações
(por exemplo ![]() ); outras variáveis podem portando ser consideradas
constantes dentro de uma região limitada de raio.
); outras variáveis podem portando ser consideradas
constantes dentro de uma região limitada de raio.
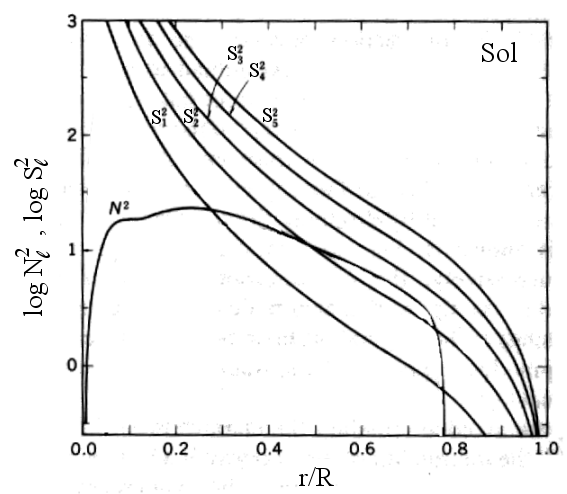

Podemos resolver para
![]() na relação de dispersão em dois limites
de ondas propagantes. Para facilitar, definimos o número de onda total,
na relação de dispersão em dois limites
de ondas propagantes. Para facilitar, definimos o número de onda total,
![]() , como
, como
![]() (como Unno et al. 1979).
A onda pode viajar em uma combinação de direções radiais e transversais.
Em uma análise local,
(como Unno et al. 1979).
A onda pode viajar em uma combinação de direções radiais e transversais.
Em uma análise local,
![]() deve ser grande.
Então, se
deve ser grande.
Então, se ![]() é muito maior do que tanto
é muito maior do que tanto ![]() quanto
quanto ![]() , e
, e ![]() é menor do que
é menor do que ![]() (como é o caso usual)
a raiz "grande" da equação (37) é:
(como é o caso usual)
a raiz "grande" da equação (37) é:
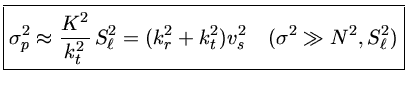 |
(38) |
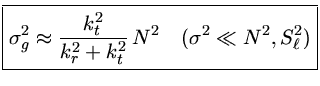 |
(39) |
Se cada modo é ortogonal em relação aos outros, então as autofunções
correspondentes a cada autovalor
![]() têm que diferir das outras em aspectos importantes.
Seguindo nossa análise local como uma aproximação,
têm que diferir das outras em aspectos importantes.
Seguindo nossa análise local como uma aproximação,
![]() e
e ![]() devem medir esta diferença. Como
devem medir esta diferença. Como ![]() é um número de onda, o comprimento de onda correspondente é
é um número de onda, o comprimento de onda correspondente é
![]() .
O número total de nodos na direção radial
(que chamamos de
.
O número total de nodos na direção radial
(que chamamos de ![]() ) na autofunção é dado por
) na autofunção é dado por
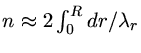 onde o "2"
conta os dois nodos por comprimento de onda. Logo
onde o "2"
conta os dois nodos por comprimento de onda. Logo
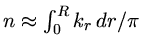 .
Se integramos a equação (38) de modo que a integral de
.
Se integramos a equação (38) de modo que a integral de
![]() aparece sozinha e então assumimos que
aparece sozinha e então assumimos que
![]() é pequeno de modo que
é pequeno de modo que ![]() pode ser desprezado (por simplicidade),
obtemos a estimativa
pode ser desprezado (por simplicidade),
obtemos a estimativa
![$ \sigma_p\approx n\pi[\int_0^R{dr\over v_s}]^{-1}$](img171.gif) |
(40) |
A estimativa correspondente para os períodos dos modos-g é
![$ { \Pi_g={2\pi\over\sigma_g}\approx n\,{2\pi^2\over[\ell(\ell+1) ]^{1/2}}[\int_0^R{N\over r}\,dr]^{-1} }$](img172.gif) |
(41) |
Os mesmos limites em ![]() em relação a
em relação a ![]() e
e ![]() também produzem as seguintes estimativas grosseiras para a razão
das autofunções radiais para tangenciais:
também produzem as seguintes estimativas grosseiras para a razão
das autofunções radiais para tangenciais:
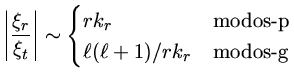
Se retirarmos a aproximação adiabática, precisamos levar em conta que calor pode ser trocado entre os elementos em movimento por pulsação. O ponto de partida é a equação de equilíbrio térmico:
![$ {\frac{\partial L_r}{\partial r}=4\pi r^2\rho[\varepsi...
...}}\frac{\partial }{\partial t}(\frac{P}{\rho^{\frac{5}{3}}})]}$](img4ad.gif) |
(1.1) |
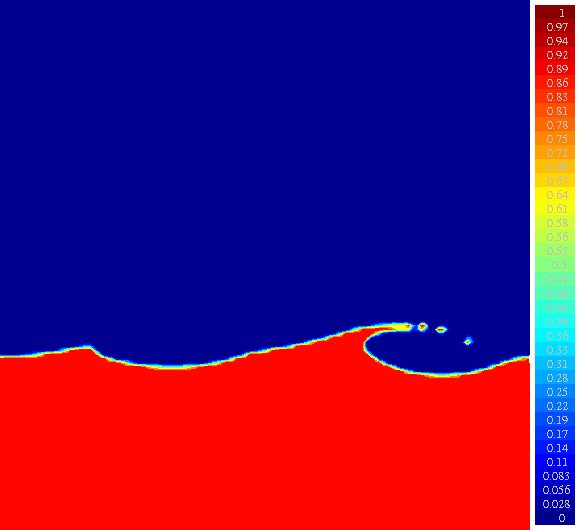
Para as variáveis clássicas, como as Cefeidas e RR Lyrae, o que causa a pulsação radial é a existência de zonas de ionização parcial do hidrogênio e do hélio. Uma zona de ionização parcial é muito opaca; os fótons são absorvidos causando a ionização do gás. Quando um gás se ioniza, o número de partículas aumenta, pois os elétrons tornam-se livres. Um aumento no número de partículas causa um aumento na pressão, que faz a camada se expandir. Mas ao se expandir, a camada se esfria e portanto as partículas têm velocidade e energia menores e podem se ligar novamente, formando átomos nêutros. Quando o gás se desioniza, diminui a número de partículas, a pressão diminui e a camada contrai. Ao se contrair, aumentando a densidade, a camada fica opaca e o processo recomeça, oscilando entre o estado expandido e contraído.
Usando a equação de continuidade de massa e o fato de
termos usado
![]() na derivação dessa equação,
pois assumimos lei dos gáses ideais, o que não é o caso de zonas
de ionização parcial, podemos escrever
na derivação dessa equação,
pois assumimos lei dos gáses ideais, o que não é o caso de zonas
de ionização parcial, podemos escrever
![$ \frac{\partial L_r}{\partial M_r} = \varepsilon - \frac{P}{\rho\l...
...rtial \ln P}{\partial t} - \Gamma_1\frac{\partial \ln \rho} {\partial t}]$](img7ad.gif) |
(1.2) |
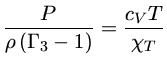
![$ \frac{\partial \ln P}{\partial t} = \Gamma_1\frac{\partial \ln \r...
...rac{\chi_T}{c_V T} [\varepsilon - \frac{\partial L_r}{\partial M_r}]$](img9ad.gif) |
(1.3) |

![$ \frac{\partial \ln T}{\partial t} = (\Gamma_3-1) \frac...
...} + \frac{1}{c_V T}[\varepsilon - \frac{\partial L_r}{\partial M_r}]$](img13ad.gif) |
(1.4) |
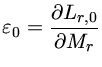
![$ \frac{\partial(\delta T/T)}{\partial t} = (\Gamma...
...v T}[\delta \varepsilon - \frac{\partial \delta L_r} {\partial M_r}]$](img23ad.gif) |
(1.5) |
![${\delta \varepsilon - \frac{\partial \delta L_r} {\partial ...
...ft[\frac{\delta T}{T} - (\Gamma_3-1)\frac{\delta \rho}{\rho}]}$](img25ad.gif) |
(1.6) |
Quando uma camada da estrela ganha energia quando comprimida, ela pode causar (drive) a pulsação. Todas as outras camadas normalmente perdem energia quando comprimidas e portanto amortecem a pulsação. A pulsação ocorre se a energia da camada que ganha energia suplanta a energia perdida em todas as outras camadas. Esta camada age como um motor a calor, transformando energia térmica em mecânica.
Se a opacidade aumenta quando a temperatura aumenta, como ocorre
em uma região de ionização parcial, a energia se acumula nesta
camada, e o elemento de massa se aquece em relação à sua
vizinhança, tornando-se instável à pulsação. Este mecanismo
de instabilidade chama-se mecanismo ![]() ,
já que representamos a opacidade por
,
já que representamos a opacidade por ![]() .
.
O mecanismo ![]() de instabilidade ocorre quando a
variação importante é no
de instabilidade ocorre quando a
variação importante é no ![]() , como ocorre no caso da segunda ionização
do hélio, quando o segundo elétron do hélio está sendo removido
ou recombinando, para temperaturas próximas de 40 000 K,
ou na ionização do hidrogênio próximo de 12 000 K.
Neste caso, a energia da compressão é absorvida parcialmente na
ionização e a temperatura não aumenta tanto quanto no
caso em que a ionização não ocorre. Desta forma a região de
ionização tende a ser um pouco mais fria que a vizinhança quando
comprimida e o calor flui para a região de ionização.
Na maioria dos casos os mecanismos
, como ocorre no caso da segunda ionização
do hélio, quando o segundo elétron do hélio está sendo removido
ou recombinando, para temperaturas próximas de 40 000 K,
ou na ionização do hidrogênio próximo de 12 000 K.
Neste caso, a energia da compressão é absorvida parcialmente na
ionização e a temperatura não aumenta tanto quanto no
caso em que a ionização não ocorre. Desta forma a região de
ionização tende a ser um pouco mais fria que a vizinhança quando
comprimida e o calor flui para a região de ionização.
Na maioria dos casos os mecanismos
![]() e
e ![]() aparecem em conjunto.
aparecem em conjunto.
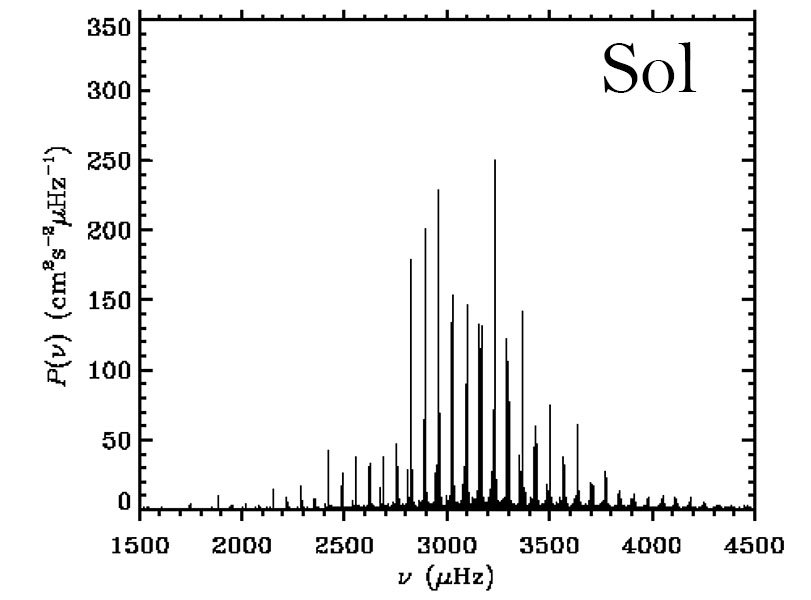
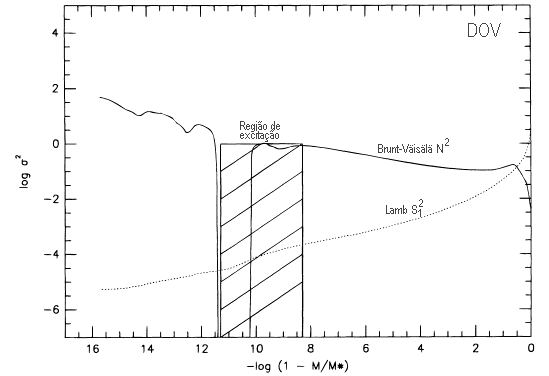
No caso do Sol e variáveis tipo solares, o mecanismo de excitação chama-se estocástico, pois há suficiente energia acústica nas camadas de convecção externas para excitar modos normais, e parte do ruído estocástico é transferido para oscilações globais.
Quais modos são selecionados para ter alta amplitude depende da localização da zona de excitação, pois não é possível colocar energia em modos com nodos naquela região. Outro fator importante é que os modos com períodos próximos da escala de tempo térmica daquela região são mais fáceis de excitar.
Em 1975 Franz L. Deubner (Astronomy & Astrophysics, 44, 371)
conseguiu resolver as oscilações solares em
modos discretos, que comparados com os modelos teóricos calculados
por Hiroyasu Ando e Yoji Osaki (1975, Publications of the Astronomical
Society of Japan, 27, 581), mostraram que as oscilações solares
com períodos da ordem de 5 minutos eram oscilações não-radiais modo-p
com
![]() entre 200 e 1000. Posteriormente, observações de
disco inteiro do Sol mostraram modos-p com
entre 200 e 1000. Posteriormente, observações de
disco inteiro do Sol mostraram modos-p com
![]() entre 1 e 200.
entre 1 e 200.
Para o Sol, os modos-p são superficiais enquanto que os modos-g são internos. Milhares de modos-p do Sol já foram observados, mas nenhum modo-g.
Um modo-p com n=1 e

 Em 1968, Arlo U. Landolt (1934-)
que estuda estrelas padrões fotométricas,
utilizando o telescópio de 2,1 m do Kitt Peak,
descobriu acidentalmente que a estrela HL Tau 76, uma anã branca,
apresentava variações de brilho com um período de 12 minutos e uma amplitude
de 0,1 magnitudes
(1968, Astrophysical Journal, 153, 151). Esta foi a primeira anã branca
variável descoberta e pertence a classe das DAV ou ZZ Cetis, com
mais de 158 variáveis conhecidas em 2011.
Em 1968, Arlo U. Landolt (1934-)
que estuda estrelas padrões fotométricas,
utilizando o telescópio de 2,1 m do Kitt Peak,
descobriu acidentalmente que a estrela HL Tau 76, uma anã branca,
apresentava variações de brilho com um período de 12 minutos e uma amplitude
de 0,1 magnitudes
(1968, Astrophysical Journal, 153, 151). Esta foi a primeira anã branca
variável descoberta e pertence a classe das DAV ou ZZ Cetis, com
mais de 158 variáveis conhecidas em 2011.
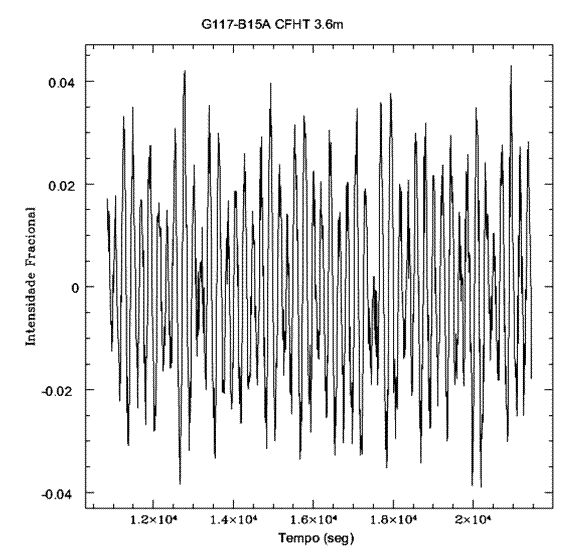
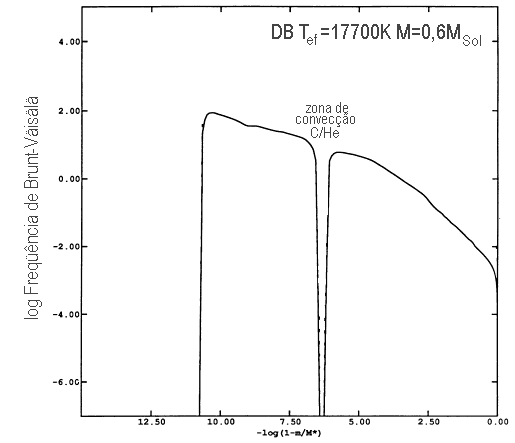
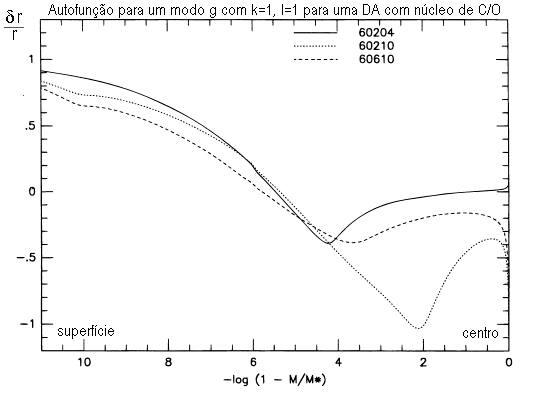
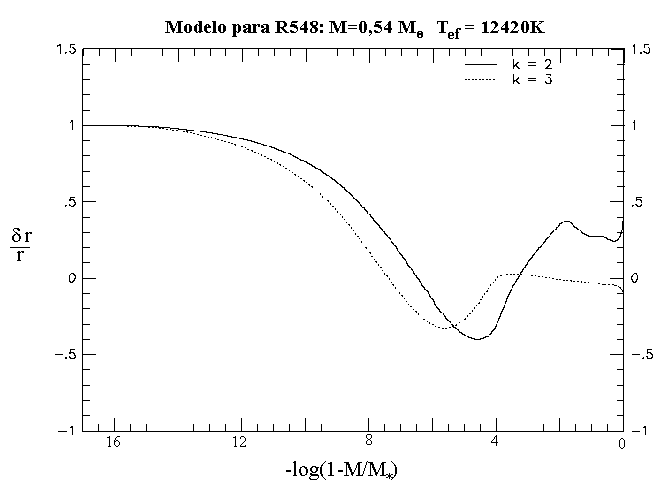
Os períodos dos modos gravitacionais dependem da variação dentro
da estrela da frequência de Brunt-Väisälä,
![]() .
Não é possível estimar seu valor facilmente, mas existem características
específicas nas estrelas anãs brancas.
Por examplo, essa frequência é muito pequena
no interior onde os elétrons estão degenerados,
e
.
Não é possível estimar seu valor facilmente, mas existem características
específicas nas estrelas anãs brancas.
Por examplo, essa frequência é muito pequena
no interior onde os elétrons estão degenerados,
e ![]() é nula para um gás completamente degenerado.
Esse não é normalmente o caso no envelope e as frequências típicas
no envelope são de várias dezenas de s-1.
é nula para um gás completamente degenerado.
Esse não é normalmente o caso no envelope e as frequências típicas
no envelope são de várias dezenas de s-1.
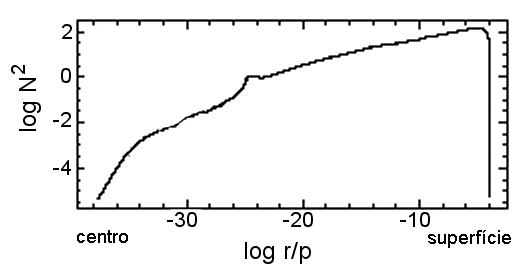
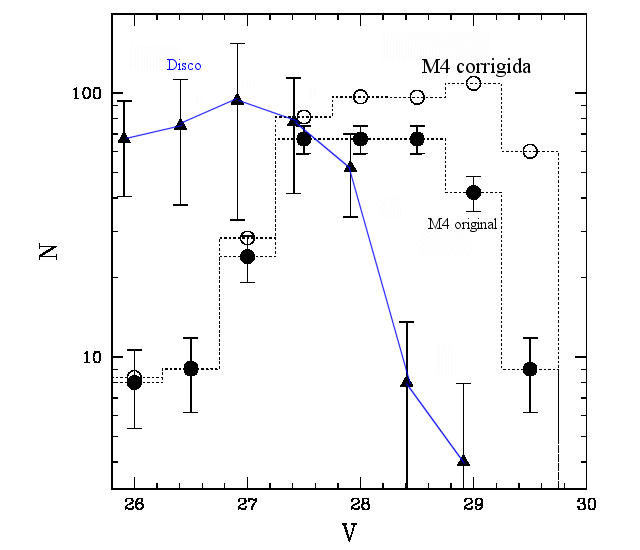
Das condições de propagação de onda, os modos-g se propagam no
envelope das anãs brancas, enquanto que os modos-p, com períodos de poucos
segundos e
ainda não observados em anãs brancas, se propagam no interior.
Este comportamento é oposto daquele para o Sol.
Desta maneira, nas anãs brancas, os modos-g oscilam na superfície mas
são excluídos do núcleo face ao baixo valor de
![]() no interior.
Os cálculos detalhados produzem valores de períodos de cerca de 100 s a
1500 s, consistentes
com os valores observados para as anãs brancas pulsantes, que têm
períodos entre 70 e 1500 s.
no interior.
Os cálculos detalhados produzem valores de períodos de cerca de 100 s a
1500 s, consistentes
com os valores observados para as anãs brancas pulsantes, que têm
períodos entre 70 e 1500 s.
Os modos de pulsação com ordens radiais baixas têm amplitude significativa em todo o interior da estrela, enquanto modos com ordens radiais altas são formados mais para fora da estrela.
A causa da instabilidade foi determinada como a mesma que excita as variáveis clássicas: está associada com as zonas de ionização parcial do hidrogênio e do hélio e, possivelmente, de carbono e oxigênio para os objetos mais quentes [Wojciech Dziembowski (1940-2025) & Detlev Koester (1981, Astronomy & Astrophysics, 97, 16), Noel Dolez & Gerard Vauclair (1981, Astronomy & Astrophysics, 102, 375), Sumner Starrfield, Arthur N. Cox, S. Hodson, & Willian D. Pesnell (1982, Conference on Pulsations in Classical and Cataclysmic Variable Stars, Boulder CO, p. 78), Donald Earl Winget, Hugh van Horn, Monique Tassoul, Gilles Fontaine (1948-2019), Carl J. Hansen (1933-2011) & Bradley W. Carroll (1982, Astrophysical Journal, 252, L65)]. O maior sucesso desta análise de excitaçãos dos modos gravitacionais em anãs brancas foi a previsão seguida da descoberta das variáveis DBs por Donald Earl Winget (Donald Earl Winget, Edward L. Robinson, R. Edward Nather (1926-2014) & Gilles Fontaine (1948-2019), 1982, Astrophysical Journal, 262, L11). Este foi o primeiro caso da existência de uma classe de variáveis que foi predita antes de sua descoberta.
Os cálculos não adiabáticos que testam a estabilidade dos modos-g são muito exitosos para as estrelas DAV e DBV, já que os cálculos ajustam razoavelmente bem com as posições observacionais da faixa de instabilidade, com uma escolha apropriada da eficiência convectiva [Paul Andrew Bradley & Donald Earl Winget 1994b; Gilles Fontaine (1948-2019), Pierre Brassard & François Wesemael (1954-2011) 1994]. Embora entendamos a causa básica da instabilidade pulsacional como resultado da zona de ionização parcial modulando o tamanho da zona de convecção durante um ciclo de pulsação, precisamos ainda de muito mais trabalho para entender os detalhes, já que a maioria dos cálculos não leva em conta a interação das pulsações com a convecção.
 Nas anãs
brancas, somente detectamos pulsações com
Nas anãs
brancas, somente detectamos pulsações com
![]() , e as variações de raio são da ordem de somente
1 metro, enquanto que as variações de temperatura, dominantes,
são da ordem de 500 K (Kepler de Souza Oliveira Filho, 1984,
Astrophysical Journal, 286, 314-327).
, e as variações de raio são da ordem de somente
1 metro, enquanto que as variações de temperatura, dominantes,
são da ordem de 500 K (Kepler de Souza Oliveira Filho, 1984,
Astrophysical Journal, 286, 314-327).
Se representarmos por ![]() a frequência de rotação de uma estrela,
e assumirmos que ela é muito menor do que a frequência de pulsação,
podemos representar a frequência de pulsação de uma oscilação de modo-g
com índices n,
a frequência de rotação de uma estrela,
e assumirmos que ela é muito menor do que a frequência de pulsação,
podemos representar a frequência de pulsação de uma oscilação de modo-g
com índices n,![]() e m como:
e m como:
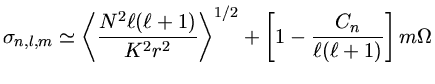
A rotação faz com que a frequência de pulsação no sentido da rotação (progrado) seja um pouco menor que o modo com m=0, que não é afetado pela rotação, enquanto o modo retrógrado tem uma frequência um pouco maior. No caso do Sol, que podemos medir suas pulsações vindas até um pouco abaixo do meio-raio, podemos medir que a rotação abaixo da zona de convecção (iniciando em 0,7 RSol) é praticamente rígida, com perído de aproximadamente 27 dias, como a que ocorre na fotosfera para latitudes de aproximadamente 35° (Michael J. Thompson, Jørgen Christensen-Dalsgaard, Mark S. Miesch & Juri Toomre. 2003, Annual Review of Astronomy & Astrophysics, 41, 599).
No site http://www.whitedwarf.org/, organizado por Travis Scott Metcalfe (1973-), é possível calcular em tempo real os períodos de pulsação dos modelos de anãs brancas DBVs.
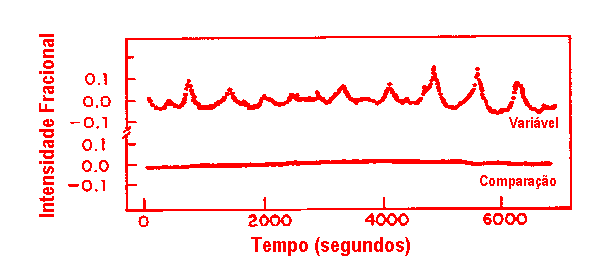
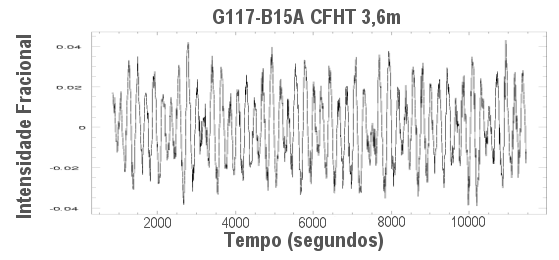
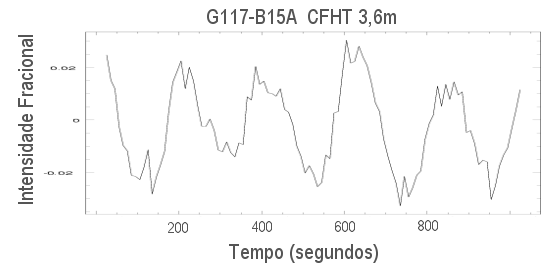
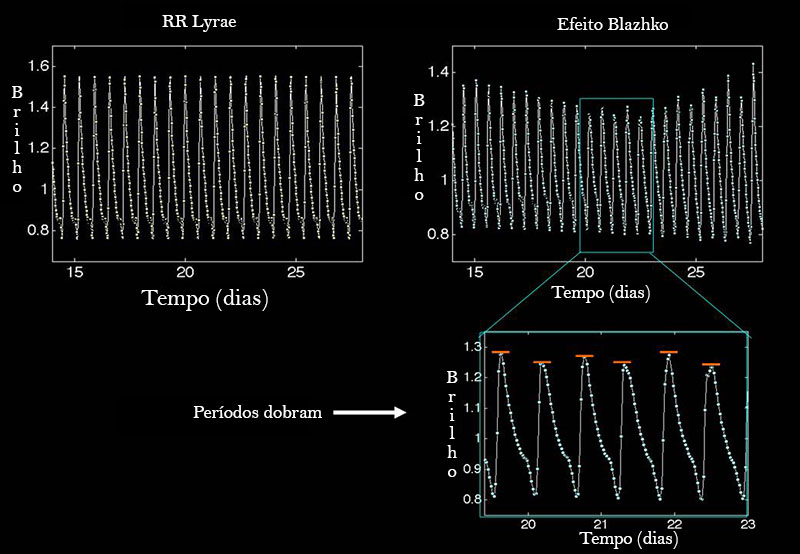
J. Robert Buchler (1942-), Marie-Jo Goupil e Carl J. Hansen (1997, Astronomy & Astrophysics, 321, 159) derivaram as equações de amplitude relacionando as interações entre as pulsações multiperiódicas não radiais, mas ressaltam que o problema é sempre em relacionar os coeficientes com o problema hidrodinâmico e de transferência de calor que nos interessa. Em primeira ordem, uma pulsação real pode ser representada como uma soma de modos normais, com amplitudes dependentes do tempo. Estas amplitudes, que assumimos variam lentamente com o tempo em comparação com as pulsações, obedecem a equações de amplitude não lineares. Embora a soma seja teoricamente infinita, assumimos que a dinâmica essencial do problema possa ser tratada somente com os primeiros termos das séries. As amplitudes e fases podem então ser relacionadas diretamente com aquelas obtidas pela análise de Fourier das observações.
No caso de duas pulsações radiais:
![$ \delta R(t) = \frac{a_1(t)}{2} \exp[i\phi_1(t)] +\frac{a_2(t)}{2} \exp[i\phi_2(t)] $](img1a.gif)
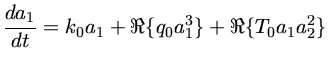
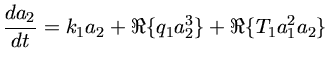

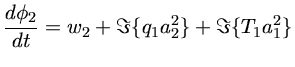
Os coeficientes de acoplamentos dependem da integral das autofunções dos modos sobre o interior da estrela. Os coeficientes serão grandes se as regiões de alta amplitude das autofunções no interior da estrela forem similares.
No caso de pulsações não-radiais, o espectro de frequências é muito mais denso, isto é, existe um número maior de frequências possíveis e, portanto, maior possibilidade de ressonâncias. Entretanto, restrições de paridade e de momentum angular podem ser usadas para eliminar vários dos possíveis acoplamentos entre os modos. Ressonâncias podem causar chaveamento de frequências, isto é, modos normais que têm frequências aproximadamente ressonantes podem ser deslocados de modo que as frequências observadas são exatamente ressonantes, acompanhados de amplitudes constantes. Estas ressonâncias podem causar o desvio do equi-espaçamento em períodos dos modos gravitacionais assintóticos (alto valor da ordem radial n). Acoplamentos ressonantes podem, portanto, ser determinantes nas amplitudes observadas, assim como nos espaçamentos entre os modos observados.
A presença de frequências que são combinações lineares das frequências normais também decorre de correções de mais alta ordem. Nos dados de 2000 do Whole Earth Telescope da DBV pulsante GD358 (Kepler de Souza Oliveira Filho, R. Edward Nather (1926-2014), Don Earl Winget, Atsuko Nitta, Scot J. Kleinman, Travis Metcalfe, Kazuhiro Sekiguchi, Jiang Xiaojun, Denis Sullivan, Tiri Sullivan, Rimvydas Janulis, Edmund Meistas, Romualdas Kalytis, Jurek Krzesinski, Waldemar Ogloza, Staszek Zola, Darragh Evelyn Anthony Adam O'Donoghue (1957-2015), Encarni Romero-Colmenero, Peter Martinez, Stefan Dreizler, Jochen Deetjen, Thorsten Nagel, Sonja L. Schuh, Gerard Vauclair, Fu Jian Ning, Michel Chevreton, Jan-Erik Solheim, Jose Miguel Gonzalez Perez, Frank Johannessen, Antonio Kanaan, José Eduardo Costa, Alex Fabiano Murillo Costa, Matt A. Wood, Nicole Silvestri, T.J. Ahrens, Aaron Kyle Jones, Ansley E. Collins, Martha Boyer, J. S. Shaw, Anjum Mukadam, Eric W. Klumpe, Jesse Larrison, Steven Daniel Kawaler, Reed Riddle, Ana Ulla & Paul Andrew Bradley. 2003, "The Everchanging Pulsating White Dwarf GD358", Astronomy & Astrophysics, 401, 639) encontramos termos de combinação linear de até quinta e sexta ordem.
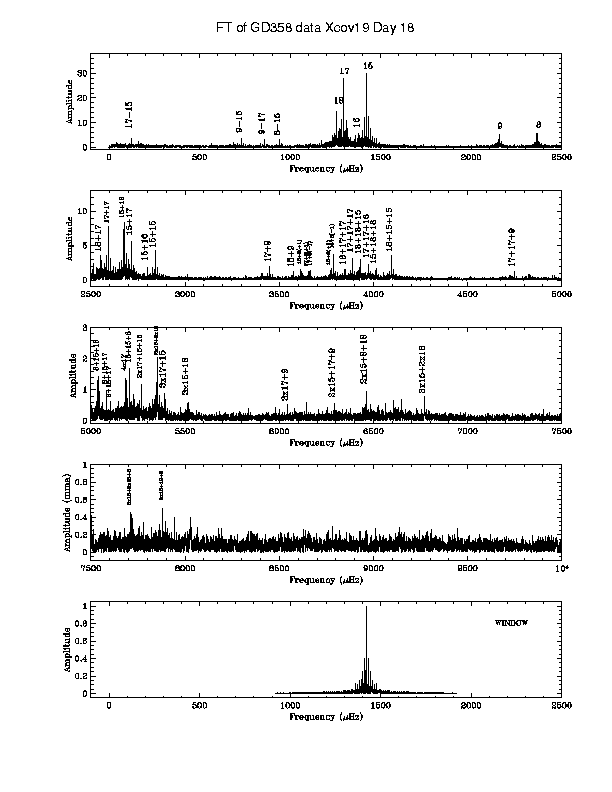
A maior parte das estrelas variáveis multi-periódicas observadas apresenta variações de amplitude em longas escalas de tempo. Por exemplo, as transformadas de Fourier das observações com o WET em anos distintos da DBV GD358 têm amplitudes diferentes, apesar da maioria das periodicidades principais estarem presentes em todos os anos. Entretanto, os dados de agosto de 1996 mostram somente uma periodicida dominante, em vez das 180 periodicidades normalmente detectadas.
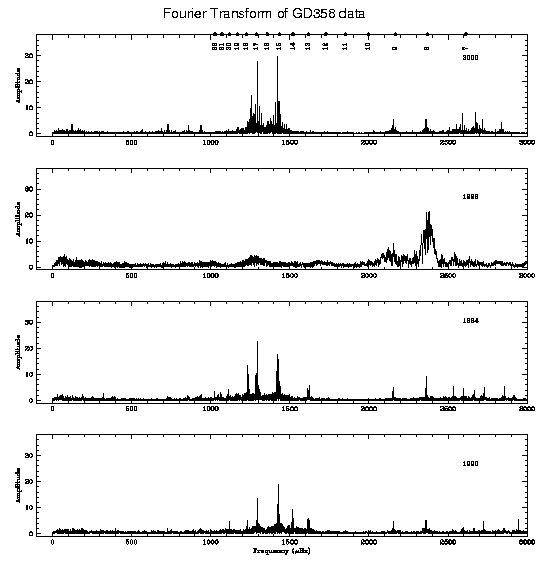
O caso mais simples de ressonância ocorre quando duas frequências
inicialmente próximas de
![]() ,
com
,
com ![]() e
e ![]() inteiros.
Existe uma solução com amplitudes e fases contantes, com
as frequências deslocadas exatamente para a igualdade
inteiros.
Existe uma solução com amplitudes e fases contantes, com
as frequências deslocadas exatamente para a igualdade
![]() .
Desta maneira
é possível que uma frequência próxima da harmônica seja trazida
para o valor da harmônica e que as amplitudes resultantes sejam
constantes.
.
Desta maneira
é possível que uma frequência próxima da harmônica seja trazida
para o valor da harmônica e que as amplitudes resultantes sejam
constantes.


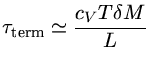
Como a amplitude do primeiro bloco de períodos é aproximadamente igual
à amplitude do segundo bloco de períodos, embora a energia cinética para o modo
![]() seja muito alta, o mecanismo de limitação de amplitudes
deve estar levando à saturação de energia, isto é, a energia no modo
é toda energia que está disponível, e não um mecanismo de limitação, como
campos magnéticos ou velocidades maiores do que a velocidade do som.
seja muito alta, o mecanismo de limitação de amplitudes
deve estar levando à saturação de energia, isto é, a energia no modo
é toda energia que está disponível, e não um mecanismo de limitação, como
campos magnéticos ou velocidades maiores do que a velocidade do som.
Como os modos "ressonantes" têm a mesma energia do modo não ressonante
![]() , então não é relevante que é mais fácil excitar um modo
ressonante, já que não existe energia disponível para excitá-los a
amplitudes mais altas.
, então não é relevante que é mais fácil excitar um modo
ressonante, já que não existe energia disponível para excitá-los a
amplitudes mais altas.
Da tese de doutorado de Donald Earl Winget, de 1981,
os primeiros modos excitados
na borda azul estão próximos de 80 a 110 s, com
![]() . Somente
quando a estrela se esfria por mais
. Somente
quando a estrela se esfria por mais
![]() K, aproximadamente, é que
o modo
K, aproximadamente, é que
o modo
![]() é excitado.
é excitado.
Portanto, para as estrelas mais quentes, o período excitado deveria
ser próximo de 100 s, como em G226-29, e nenhum outro deveria estar
excitado. Tendo em vista que leva cerca de ![]() anos para a estrela
esfriar
anos para a estrela
esfriar ![]() K,
e a escala de crescimento das pulsações é de semanas
ou meses, a estrela não deveria ter o modo
K,
e a escala de crescimento das pulsações é de semanas
ou meses, a estrela não deveria ter o modo
![]() excitado.
excitado.
Um modo com
![]() tem um cancelamento geométrico muito maior,
de acordo com os cálculos de
Wojciech Dziembowski (1977, Acta Astronomica, 27, 203) e
Edward Lewis Robinson (1945-), Kepler de Souza Oliveira
Filho (1956-) e R. Edward Nather (1926-) publicados em
1982 no Astrophysical Journal, 259, 219.
O fator de diluição geométrica é da ordem de
0,26 para
tem um cancelamento geométrico muito maior,
de acordo com os cálculos de
Wojciech Dziembowski (1977, Acta Astronomica, 27, 203) e
Edward Lewis Robinson (1945-), Kepler de Souza Oliveira
Filho (1956-) e R. Edward Nather (1926-) publicados em
1982 no Astrophysical Journal, 259, 219.
O fator de diluição geométrica é da ordem de
0,26 para ![]() , 0,04 para
, 0,04 para ![]() e 0,02
para
e 0,02
para ![]() , pois vemos o disco integrado e as várias regiões
quentes e frias na superfície da estrela se cancelam.
, pois vemos o disco integrado e as várias regiões
quentes e frias na superfície da estrela se cancelam.
Embora a estrela G226-29 tenha amplitude muito pequena, 6 mma,
a análise das pulsações com o Hubble Space Telescope por
Kepler de Souza Oliveira Filho, Edward L. Robinson, Detlev Koester,
J. Christopher Clemens, R. Edward Nather e Xian Jian Jiang
(2000, "Mode Identification of Pulsating White Dwarfs using the HST",
Astrophysical Journal, 539, 379-391) em que compararam a amplitude no
ótico com a amplitude de pulsação no ultravioleta, demonstrou que
a pulsação com período de 109 s é na verdade um modo com
![]() .
.
A estrela G185-32 é ainda mais problemática, já que os dados do Telescópio Espacial Hubble indicam que a periodicidade em 141 s não muda de amplitude significativamente do ultravioleta para o ótico e, portanto, não fita nenhum modelo teórico (Bárbara Garcia Castanheira, Kepler de Souza Oliveira Filho, Pawel Moskalik, Scot J. Kleinman, A. E. Sansom, Jan-Erik Solheim, J. A. Belmonte, Steven Daniel Kawaler, Antonio Kanaan, Don Earl Winget, R. Edward Nather, Todd K. Watson, J. Christopher Clemens, Judith Provencal, Albert D. Grauer, Paul Andrew Bradley, Matt A. Wood, N. Achilleos, Gerard Vauclair, Benoite Pfeiffer, Michael Chevreton, Noel Dolez, B. Serre, J. S. Yang, Fu Jian Ning, T. M. K. Marar, B. N. Ashoka, Edmund Meistas, A. V. Chernyshev, Tsevi Mazeh, Elia Leibowitz, Jerzy Krzesinski, Gabriel Pajdosz, Staszek Zola & José Eduardo da Silveira Costa. 2004, "Observations of the Pulsating White Dwarf G 185-32", Astronomy & Astrophysics, 413, 623). Entretanto Jörg Ising e Detlev Koester (2001, Astronomy & Astrophysics, 374, 116) sugerem que efeitos não lineares na atmosfera transformam os modos normais descritos por harmônicos esféricos na base da zona de ionização parcial em modulações complexas, não descritas por harmônicos esféricos, na superfície, mas somente para amplitudes maiores que 5%, o que não é o caso.
 Peter Goldreich, Yanqin Wu & Marten van Kerkwijk
Peter Goldreich, Yanqin Wu & Marten van KerkwijkYanqin Wu e Peter Goldreich (1999, Astrophysical Journal, 519, 783) e Yanqin Wu (2001, Monthly Notices of the Royal Astronomical Society, 323, 248) levam em conta a interação entre a pulsação e a convecção e propõem que as não linearidades causam a presença de harmônicos e combinações lineares na transformada de Fourier, mas que as amplitudes dos harmônicos são sempre menores do que as amplitudes dos picos combinações lineares, se as componentes têm a mesma amplitude.
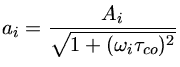
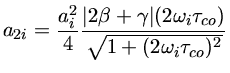
![$ a_{i+j} = \frac{n_{ij}}{2} \frac{a_i a_j}{2}
\frac{ \vert 2\beta...
...a_i\pm \omega_j)\tau_{co}}
{\sqrt {1+ [(\omega_i \pm \omega_j)\tau_{co}]^2 }} $](img28a.gif)
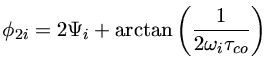
![$ \phi_{i+j} = (\Psi_i\pm \Psi_j) + \arctan[\frac{1}{(\omega_i\pm \omega_j) \tau_{co}}] $](img31a.gif)
Antony J. Brickhill (1992, Monthly Notices of the Royal Astronomical Society, 259, 529) estuda a interação entre as pulsações e a convecção, levando em conta que a escala de tempo de convecção é da ordem de 1 s e, portanto, a convecção se ajusta instantaneamente à pulsação. Ele calcula que a variação de temperatura na superfície é não sinusoidal e, portanto, a variação de luminosidade também não é. Ele também deduz que a viscosidade turbulenta reduz a pulsação porque não permite grandes movimentos horizontais.
Pierre Brassard,
Gilles Fontaine (1948-2019) e Francois Wesemael (1954-2011) (1995, Astrophysical Journal Supplement
Series, 96, 545) calculam o fluxo emergente a partir de uma variação
de temperaturas sinusoidal na base da zona de ionização parcial.
Os efeitos não lineares aparecem somente devido ao transporte
radiativo de energia. Eles calculam que o efeito de cancelamento
geométrico (soma de zonas quentes e zonas frias sobre o disco
visível) é de 0,43 para ![]() , 0,0639 para
, 0,0639 para ![]() e 0,0395
para
e 0,0395
para ![]() em luz branca.
em luz branca.
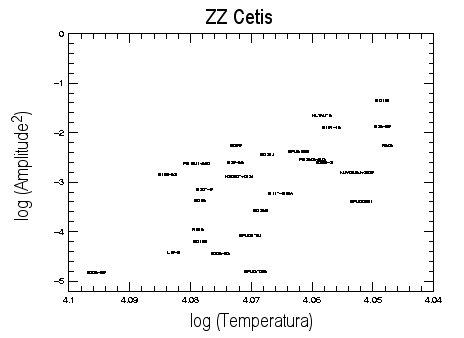
A concentração de estrelas no primeiro bloco de períodos,
próximo da borda azul (quente) da faixa de instabilidade,
descoberta por J. Christopher Clemens e
confirmada por Antonio Kanaan e Anjum Mukadam, também indica
que as estrelas devem ter a mesma massa,
ou os períodos teriam que ser diferentes.
A massa da camada de hidrogênio também deve ser similar, mas os
períodos não são muito dependentes desta massa. Todos os modos
neste bloco de 220 s deveriam ser modos com
![]() .
Um projeto que precisa ser executado é procurar por modos com
.
Um projeto que precisa ser executado é procurar por modos com
![]() e, portanto, de baixa amplitude, na borda azul da
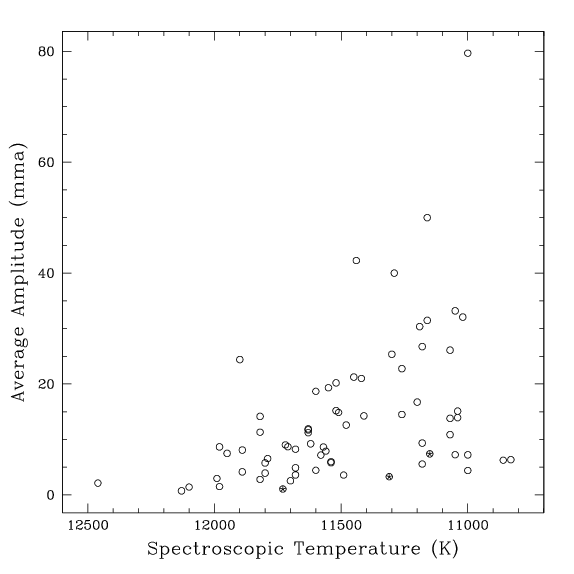
faixa de instabilidade. Antonio Kanaan, na sua tese de doutorado em 1996,
demonstrou que não existem estrelas com baixa amplitude mais
frias que a borda
vermelha da faixa de instabilidade. Na verdade a amplitude dos
modos cai pelo menos por um fator de 40, já que o limite de
detecção alcançado por ele foi de 5 mma, e as estrelas
variáveis na borda vermelha têm em média uma amplitude 40 vezes
maior
(Antonio Kanaan, Kepler de Souza Oliveira Filho e Don Earl Winget, 2002,
"The ZZ Ceti red edge", Astronomy & Astrophysics, 389, 896).
e, portanto, de baixa amplitude, na borda azul da
faixa de instabilidade. Antonio Kanaan, na sua tese de doutorado em 1996,
demonstrou que não existem estrelas com baixa amplitude mais
frias que a borda
vermelha da faixa de instabilidade. Na verdade a amplitude dos
modos cai pelo menos por um fator de 40, já que o limite de
detecção alcançado por ele foi de 5 mma, e as estrelas
variáveis na borda vermelha têm em média uma amplitude 40 vezes
maior
(Antonio Kanaan, Kepler de Souza Oliveira Filho e Don Earl Winget, 2002,
"The ZZ Ceti red edge", Astronomy & Astrophysics, 389, 896).
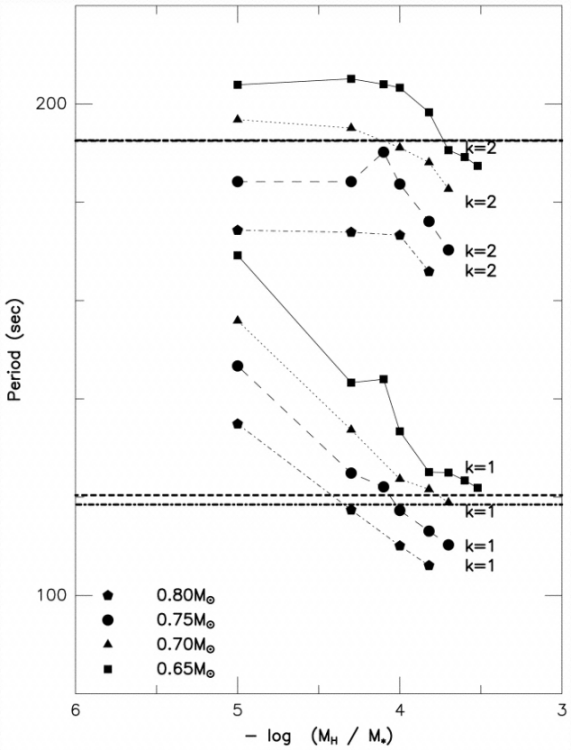
Quando a estrela esfria e o modo com
![]() é excitado, o modo
com menor período desaparece? Tanto L19-2 quanto G117-B15A têm modos
excitados tanto próximos de 100 s quanto próximos de 220 s, de modo
que aparentemente os modos com menor período permanecem excitados.
Entretanto, os modos de curto período podem ser somente devido a
ressonâncias do modo principal, já que em G117-B15A, G185-32, GD385,...
os modos de período curto são harmônicos. Mas o modo de período mais
curto em G185-32, de 70s, não é um harmônico.
é excitado, o modo
com menor período desaparece? Tanto L19-2 quanto G117-B15A têm modos
excitados tanto próximos de 100 s quanto próximos de 220 s, de modo
que aparentemente os modos com menor período permanecem excitados.
Entretanto, os modos de curto período podem ser somente devido a
ressonâncias do modo principal, já que em G117-B15A, G185-32, GD385,...
os modos de período curto são harmônicos. Mas o modo de período mais
curto em G185-32, de 70s, não é um harmônico.
Como a zona de ionização parcial é a causa da pulsação (driving zone), as amplitudes devem crescer na escala de tempo evolucionária, já que, nesta escala de tempo, a zona de ionização parcial está se deslocando para dentro da estrela.
Como a energia térmica na zona de convecção cresce exponencialmente quando a zona de ionização parcial vai se aprofundando, a energia disponível para pulsação cresce exponencialmente.
Ressonância entre modos não pode ser o efeito principal nas pulsações das anãs brancas porque, para os modos-g, o número de modos possíveis decresce com o aumento da frequência (modos igualmente espaçados em período). Nos dados de 1994 de GD358, 62 combinações lineares foram identificadas por Francois Vuille et al. (2000, Monthly Notices of the Royal Astronomical Society, 313, 185) que mostrou também que a maior parte das periodicidades com combinações lineares tem a mesma fase que os modos normais geradores. Estas fases são compatíveis com distorções de forma e estão em concordância com os modelos de Yanqin Wi & Peter Goldreich e de Antony J. Brickhill para a resposta não linear da zona de convecção.
Marten Henric van Kerkwijk (1966-), J. Christopher Clemens & Yanqin Wu (2000, Monthly Notices of the Royal Astronomical Society, 314, 209) demonstraram que para a DAV G29-38, as combinações lineares não apresentam velocidades horizontais, enquanto os modos normais apresentam. Isto indica que os modos normais e as combinações lineares não têm a mesma origem física e, portanto, excitação não linear não é a causa das periodicidades em combinações lineares, pelo menos para esta ZZ Ceti.
Quando a amplitude de pulsação cresce até atingir proporções não lineares, um modo normal deixa de ser descrito como um esférico harmônico. A descrição matemática das pulsações necessita de termos em combinações lineares de outros esféricos harmônicos, de modo que os termos em combinações lineares não são, neste caso, modos de pulsação independentes. Mas Kepler de Souza Oliveira Filho, em seu artigo de 1984, "The ZZ Ceti Star GD 385 Revisited", publicado no Astrophysical Journal, 278, 754, demonstrou que o "harmônico" na estrela GD385 é de fato um modo independente.
Quando levamos em conta os efeitos não adiabáticos, escrevermos a frequência de uma pulsação como
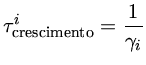
Nos modelos não adiabáticos de Brickhill e de Goldreich & Wu de
anãs brancas, modos com valores intermediários de ![]() e
e ![]() são os que mais são excitados, porque
suas autofunções têm um gradiente espacial muito pequeno na base
da zona de convecção, de modo que têm um bloqueio convectivo muito
pequeno.
Nestes modelos, se
são os que mais são excitados, porque
suas autofunções têm um gradiente espacial muito pequeno na base
da zona de convecção, de modo que têm um bloqueio convectivo muito
pequeno.
Nestes modelos, se ![]() for a escala de tempo térmica da zona
de excitação (driving) das pulsações, somente pulsações
com períodos
for a escala de tempo térmica da zona
de excitação (driving) das pulsações, somente pulsações
com períodos
![]() são excitadas e, portanto,
o máximo período das pulsações das anãs brancas DAVs nestes
modelos é da
ordem de 1000 segundos (Anthony J. Brickhill 1991,
Monthly Notices of the Royal Astronomical Society, 252, 334).
Yanqin Wu & Peter Goldreich, em seu artigo
de 1999 no Astrophysical Journal, 519, 783 obtém um período
máximo de 1400 s, próximo do valor observacional de 1500 s,
para o máximo período que a zona de convecção consegue transmitir.
são excitadas e, portanto,
o máximo período das pulsações das anãs brancas DAVs nestes
modelos é da
ordem de 1000 segundos (Anthony J. Brickhill 1991,
Monthly Notices of the Royal Astronomical Society, 252, 334).
Yanqin Wu & Peter Goldreich, em seu artigo
de 1999 no Astrophysical Journal, 519, 783 obtém um período
máximo de 1400 s, próximo do valor observacional de 1500 s,
para o máximo período que a zona de convecção consegue transmitir.
Nas teorias lineares de ressonâncias, as combinações de três ou mais frequências devem ter amplitudes muito menores do que as combinações de duas frequências, porque envolvem coeficientes de mais alta ordem.
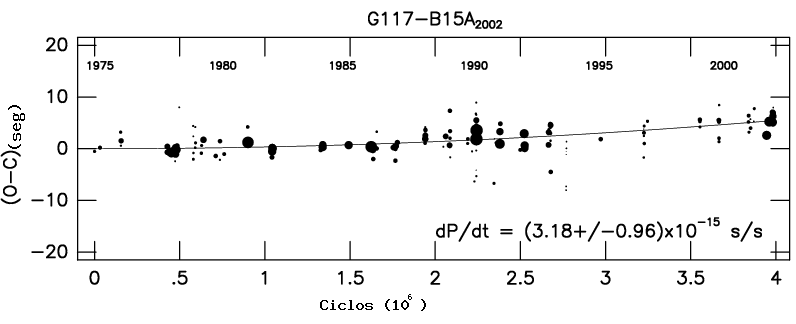
Para uma anã branca ser uma DA em 20 000 K e log g=8, somente 0,1 g cm-2 é necessário para atingir a profundidade ótica de Rosseland 100, ou seja, uma camada de somente 3×10-6 MSol de hidrogênio. Entretanto para que uma DA seja contaminada pelo He trazido à superfície em Tef~10 000 K pela zona de convecção em expansão, a camada de hidrogênio necessitaria ser mais fina que MH=10-10M*, o que não é consistente com as massas de hidrogênio determinada pelas pulsações.
Uma anã branca no disco velho ou no halo deverá acretar cerca de
MH= 10-10 MSol
em 4×108 anos (idade para chegar a 20 000 K),
para uma densidade de hidrogênio média de 0,01 cm-3.
O artigo de Marie-Jo Goupil, Michel Auvergne, & Annie Baglin, 1991, Astronomy & Astrophysics, 250, 89, trata do uso de wavelets para estudar a variação de amplitude com o tempo das pulsações das anãs brancas.
Hannah Quaintrell, Andrew J. Norton, T. D. C. Ash, Paul Roche, Bart Willems, Tim R. Bedding, Ivan K. Baldry, e Rob P. Fender publicaram no Astronomy & Astrophysics, 401, 313 (2003) uma possível detecção de oscilações não radiais induzidas por forças de maré na estrela companheira da estrela de nêutrons Vela X-1.
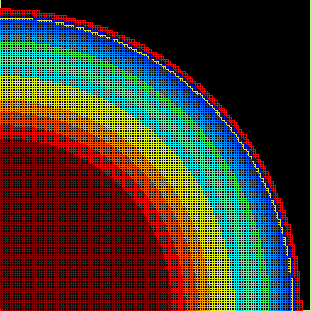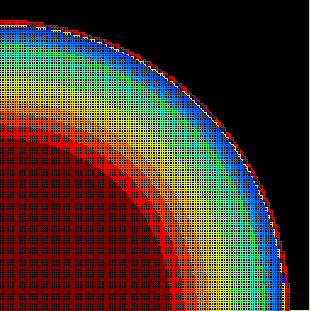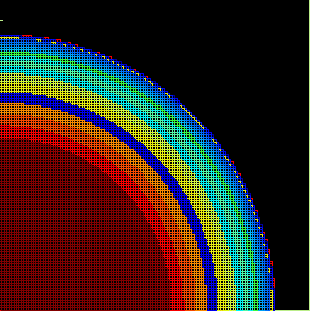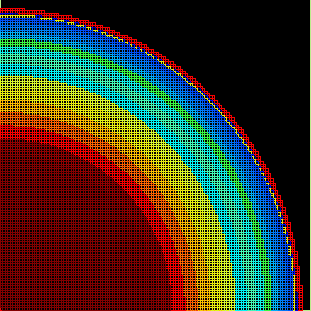

Para o Sol, as pulsações, não-radiais, resultam em uma profundidade do envelope convectivo de 0,713 ± 0,003, já que a incerteza na velocidade do som é somente 0,003. As novas determinações de abundância do Sol, reduziram C,O, N em 30%, resultando em Z/X=0,017, mas o valor antigo de 0,023 fita melhor a sismologia.
Subrahmanyan Chandrasekhar (1910-1995) em seus artigos de 1964, Dynamical instability of gaseous masses approaching the Schwarzschild limit in general relativity}, publicados no Physical Review Letters}, 12, 114 e Astrophysical Journal, 140, 417, desenvolveu a teoria de pulsações estelares na relatividade geral.
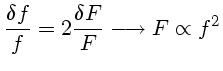
Bradley, Paul Andrew, & Dziembowski, W.A. 1996, ApJ, 462, 376.
Brunt, David 1927, The period of simple vertical oscillations in the atmosphere. Quart. J. Roy. Meteorol. Soc., 53, 30-32.
Bradley, Paul, & Winget, Don Earl 1994a, ApJ, 430, 850.
Clement, C., 1997, Catalogue of variable Stars in Globular Clusters, Fourth Edition, (Publications of the David Dunlab Obs.: Toronto:Canada).
Cox, John Paul (1926-1984), 1980, Theory of Stellar Pulsation, (Princeton: Princeton University Press).
Dolez, Noel, & Vauclair, Gerard 1981, A&A, 102, 375.
Dziembowski, Woytek, and Koester, Detlev 1981, A&A, 97, 16.
Eddington, Arthur Stanley (1882-1944) 1917, Observatory, 40, 209.
Fontaine, Gilles (1948-2019), Brassard, Pierre, & Wesemael, Francois (1926-2014) 1994, ApJ, 428, L61.
Hansen, Carl John (1933-2011), & Kawaler, Steven Daniel, 1994, Stellar Interiors, (Springer-Verlag: Berlin).
Hine, Butler H., & Nather, R.Edward (1926-2014), 1987, in Proceedings of IAU Colloq. No. 95, The Second Conference on Faint Blue Stars, A.G. Davis Philip, D.S. Hayes, & J.W. Liebert, (L.Davis Press: Schenectady), p. 619.
Kawaler, Steven Daniel 1988, ApJ, 334, 220.
Kawaler, Steven Daniel, Winget, Don Earl, Hansen, Carl John (1933-2011), and Iben, Icko Jr. (1931-) 1986, ApJ, 306, L41.
Kholopov, P.N., 1998, General Catalogue of Variable Stars, Fourth Edition, (Nauka: Moscow).
Lamb, H. 1910, On the theory of waves propagated vertically in the atmosphere. Proc. London Math. Society, 7, 122-141..
Ledoux, Paul (1914-1988), 1958, in Handbuch der Physik, S. Flügge, (Berlin: Springer-Verlag), p. 51, 605-682.
Ledoux, P., and Walraven, Th., 1958, in Handbuch der Physik, S. Flügge, (Berlin: Springer-Verlag), p. 51, 353-601.
Leavitt, H.S. 1912, Harvard Circ., 1912, 173.
Rayleigh, Lord 1883, Investigation of the character of the equilibrium of an incompressible heavy fluid of variable density. Proc. London Math. Society, 14, 170-177.
Ritter, A. 1879, Weidemanns Ann., 8, 179.
Ritter, A. 1879, Weidemanns Ann., 13, 366.
Rossby, C.-G. 1940, Planetary flow patterns in the atmosphere. Quart. J. Roy. Meteorol. Soc., 66, 68-87.
Starrfield, Sumner, Cox, Arthur Nelson, Kidman, R., and Pesnell, William Dean 1985, ApJ, 293, L23.
Starrfield, Sumner G., Cox, Arthur Nelson, Hodson, S., and Pesnell, William Dean, 1982, in Pulsations in Classical and Cataclysmic Variable Stars, J.P. Cox & C.J. Hansen, (Boulder: Joint Institute for Laboratory Astrophysics), p. 46.
Unno, W., Osaki, Y., Ando, H., and Shibahashi, Hiromoto., 1979, Nonradial Oscillations of Stars, (Tokyo: University of Tokyo Press).
Unno, W., Osaki, Y., Ando, H., Saio, Hideiuki, and Shibahashi, Hiromoto, 1989, Nonradial Oscillations of Stars, 2nd ed., (Tokyo: University of Tokyo Press).
Väisälä, V. 1925, Uber die Wirkung der Winschankungen auf die Pilotbeobachtungen. Soc. Sci. Fenn, Commentat. Phys.-Math, 2, 19-37.
Winget, Don Earl, 1981, Gravity Mode Instabilities in DA White Dwarfs, (Ph.D. Dissertation: University of Rochester, Rochester, N.Y).
Winget, Don Earl, Robinson, Edward Lewis, Nather, R. Edward (1926-2014), and Fontaine, Gilles (1948-2019) 1982b, ApJ, 262, L11.