- O semi-eixo maior da órbita do planetóide 1982RA é de 1,568 UA.
- Se em 8 de outubro de 1982 a distância ao Sol desse objeto era 1,17 UA,
qual a sua velocidade nessa data?
- Qual o período desse objeto?
- Um satélite é lançado a 300 km de altura da superície da
Terra, com velocidade paralela á superfície.
- Qual o valor de sua
velocidade para descrever uma órbita circular?
- E para descrever uma órbita parabólica?
- E para descrever uma órbita elíptica com excentricidade 0,05 e
perigeu no ponto de lançamento?
- Qual a velocidade de escape da Terra
(
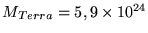 kg,
kg, 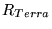 = 6370 km),
para uma partícula na sua superfície? E para uma partícula a
1000 km de sua superfície?
= 6370 km),
para uma partícula na sua superfície? E para uma partícula a
1000 km de sua superfície?
- Qual é raio de um buraco negro com massa igual à massa da Terra ?
- Calcule a velocidade orbital média da Terra e o seu momentum angular orbital.
- Considere um cometa com uma distância no afélio de
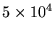 UA
e uma excentricidade orbital de 0,995.
UA
e uma excentricidade orbital de 0,995.
- Qual é a distância do cometa ao sol no perihélio?
- Qual o seu período orbital?
- Quais suas velocidades no perihélio e no afélio?
- Quanto vale o momentum angular orbital do cometa?
-
A partir da equação da órbita
 onde r, a , e
onde r, a , e 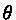 são definidos como na figura,
são definidos como na figura,
mostre que, para 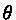 = 0° e
= 0° e 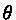 = 180°, essa equação dá a posição do
periélio (r = a(1-e)) e do afélio (r=a(1+e)), respectivamente.
= 180°, essa equação dá a posição do
periélio (r = a(1-e)) e do afélio (r=a(1+e)), respectivamente.
- A partir da segunda lei de Kepler, prove que o momentum angular de um
planeta vale:
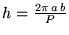 . Então use o conceito de
momentum angular
. Então use o conceito de
momentum angular
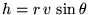 = constante, onde
= constante, onde 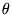 é o ângulo entre o vetor posição
é o ângulo entre o vetor posição 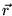 e o vetor velocidade
e o vetor velocidade
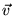 , para mostrar que as velocidades no afélio e no periélio
valem, respectivamente;
, para mostrar que as velocidades no afélio e no periélio
valem, respectivamente;
e
Qual a razão
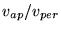 para a Terra?
para a Terra?
- A trajetória elíptica de menor energia para uma espaçonave ir
de um planeta a outro não é uma linha reta, mas sim uma órbita
elíptica em torno do Sol, cujo
periélio toca a órbita do planeta mais interno e cujo afélio
toca a órbita do planeta mais externo. Para uma trajetória assim
entre a Terra e Saturno, sabendo que o raio médio da órbita da
Terra é 1 UA e o raio médio da órbita de Saturno é 9,5 UA,
calcule:
- o semi-eixo maior da órbita
- o tempo de viagem (ida e volta)
- a velocidade no lançamento (periélio)
- a velocidade no afélio
- Calcule a razão entre a força de maré na Terra, causada pelo Sol,
e a força de maré na Terra, causada pela Lua. Qual é a
maior? Quantas vêzes é maior?
- Calcule razão entre a força de maré na Lua, causada pela Terra,
e compare com a força de maré na Terra, causada pela Lua. Qual é a
maior? Quantas vêzes é maior?
- Se a maré alta, hoje, acontece ao meio dia, a que horas ocorrerá
a próxima maré alta? E a seguinte?
- O que é precessão? Qual o seu efeito na posição das estrelas?
Ela tem efeito nas estações? Explique. Por que o ponto Áries
tem esse nome se ele se localiza na constelação de Peixes?
- Explique por que um satélite grande tem
uma probabilidade maior
de ser quebrado pelas forças de maré do que um satélite pequeno.
- Quais os dois tipos básicos de planetas encontrados no sistema solar? Quais
as diferenças básicas dos dois tipos?
- Liste os nomes dos planetas do sistema solar, em ordem de distância ao Sol.
Descreva os aspectos básicos da hipótese nebular para a formação do sistema solar, e dê três exemplos de como essa teoria explica alguns aspectos observados
atualmente no sistema solar.
- Seja um átomo de massa
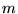 na atmosfera de um planeta de massa
na atmosfera de um planeta de massa 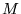 , raio
, raio 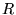 e temperatura atmosférica
e temperatura atmosférica 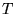 . Sabendo que a energia cinética média
das partículas de um gás é dada pela expressão
. Sabendo que a energia cinética média
das partículas de um gás é dada pela expressão
onde 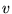 é a velocidade média das partículas, e
k = 1,38
é a velocidade média das partículas, e
k = 1,38
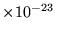 J/K, deduza uma expressão para a temperatura
mínima da atmosfera do planeta para que os átomos de massa
J/K, deduza uma expressão para a temperatura
mínima da atmosfera do planeta para que os átomos de massa 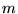 escape
de seu campo gravitacional. Expresse essa temperatura em termos de
escape
de seu campo gravitacional. Expresse essa temperatura em termos de 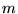 ,
, 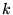 e
e
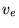 , a velocidade de escape do planeta.
, a velocidade de escape do planeta.
Calcule a temperatura máxima que a Terra deveria ter para ter hidrogênio
atômico (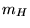 = 1,6
= 1,6
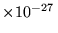 kg em sua atmosfera. E a
temperatura mínima para que o oxigênio(
kg em sua atmosfera. E a
temperatura mínima para que o oxigênio(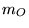 = 16
= 16 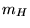 ) escapasse
de sua atmosfera.
) escapasse
de sua atmosfera.
- Cientistas calculam que o impacto ocorrido em 1908, em Tunguska, liberou uma energia
de 15 Megatons (1 ton = 4,2
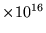 ergs).Qual o tamanho provável do
asteróide impactante?
Suponha que a densidade do asteróide é 3 g/cm
ergs).Qual o tamanho provável do
asteróide impactante?
Suponha que a densidade do asteróide é 3 g/cm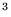 , e que a velocidade
do asteróide no impacto era igual à velocidade de escape da Terra.
, e que a velocidade
do asteróide no impacto era igual à velocidade de escape da Terra.
 onde r, a , e
onde r, a , e 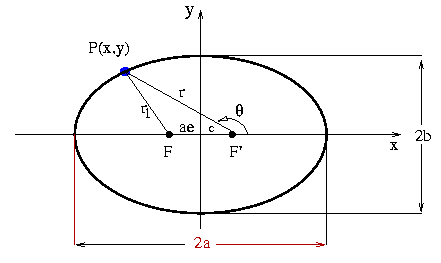
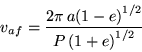
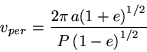
![]() para a Terra?
para a Terra?
![]() é a velocidade média das partículas, e
k = 1,38
é a velocidade média das partículas, e
k = 1,38
![]() J/K, deduza uma expressão para a temperatura
mínima da atmosfera do planeta para que os átomos de massa
J/K, deduza uma expressão para a temperatura
mínima da atmosfera do planeta para que os átomos de massa ![]() escape
de seu campo gravitacional. Expresse essa temperatura em termos de
escape
de seu campo gravitacional. Expresse essa temperatura em termos de ![]() ,
, ![]() e
e
![]() , a velocidade de escape do planeta.
, a velocidade de escape do planeta.
![]() = 1,6
= 1,6
![]() kg em sua atmosfera. E a
temperatura mínima para que o oxigênio(
kg em sua atmosfera. E a
temperatura mínima para que o oxigênio(![]() = 16
= 16 ![]() ) escapasse
de sua atmosfera.
) escapasse
de sua atmosfera.