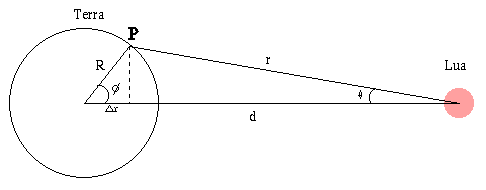
Considere a atração gravitacional FP, sentida por uma partícula em um ponto P na superfície da Terra, situado a uma distância r da Lua. Seja d a distância centro a centro entre Terra e Lua, e R o raio da Terra.
A força diferencial 
no ponto P em relação ao centro da
Terra, FC, é:
Como a distância da Lua ao ponto, r, é muito maior do que o raio da Terra, R,
o ângulo θ
é muito pequeno e
a direção da força 
é quase paralela direção à da
força 
e,
portanto, se pode dizer sem muita perda de precisão que
O valor de já foi obtido na
seção 1 e
vale
Nesta expressão, M é a massa do corpo que provoca a maré (a Lua no
nosso exemplo), m é a massa elemento de massa (partícula teste), r é
a distância do ponto onde estou
medindo a maré ao corpo provocador da
maré, isto é, entre M e m, (em média, a distância Terra-Lua, ou d na figura),
e
é a distância entre o ponto e o centro de massa
(R cosΦ na nossa figura, onde R é o raio da Terra).
Considerando que a força gravitacional média da Lua sobre a Terra está aplicada no centro da Terra, a variação máxima nessa força acontece para os pontos que estão sobre a superfície da Terra, na direção da linha que une os centros da Terra e da Lua, Φ=0. A diferença de distância entre esses pontos e o centro da Terra é o próprio raio da Terra, R, e, conseqüentemente, a máxima aceleração de maré na Terra, devido à Lua, é
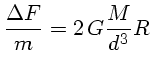
A força pode ser decomposta em uma componente vertical à
superfície da Terra, e uma componente horizontal. A componente vertical
provoca apenas uma leve variação do peso das massas localizadas no ponto
onde estamos calculando a força de maré; é a componente horizontal
que provoca a maré propriamente dita.
Próxima: Comparação das marés da Lua e do Sol Volta: Forças Gravitacionais Diferenciais
