Altura do bojo de maré

Seja a_L a aceleração gravitacional de uma partícula de massa m na superfície da Terra, causada pela Lua, elevando-a uma altura h_L.

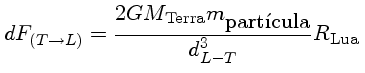
Se considerarmos que a

energia potencial=m g h_L

causada pelo deslocamento h_L devido à maré da Lua sobre uma massa m tem que ser equilibrado pelo

trabalho realizado pela força de maré devido à Lua na superfície da Terra (em R_T) = m da_L R_T

temos então:

m g h_L = m da_L R_T

e

h_L = (da_L ⁄ g)R_T

Sendo g a aceleração gravitacional na superfície da Terra:

g = GM_TR_T²
= 9,81 N/kg

e da_L a aceleração de maré devido à Lua na Terra:

da_L = 2 G M_L R_T ⁄ d_T-L³

então

h_L = 2 (M_L ⁄ M_T)( R_T⁴ ⁄ d_T-L³)

Obtemos:

e similarmente para a maré do Sol:

As marés, a rotação sincronizada da Lua e a evolução do sistema Terra-Lua

A força de maré causada em uma partícula na Lua, pela Terra, é dada por:

$d F_{(T-L)} = \frac{2GM_{Terra}m_{particula}}{d_{L-T}^3} R_{Lua}$

e a força de maré causada em uma partícula na Terra, pela Lua, é dada por:

$d F_{(L-T)} = \frac{2GM_{Lua}m_{particula}}{d_{L-T}^3} R_{Terra}$

$dF_{(T\rightarrow L)} \simeq 20 dF_{(L\rightarrow T)}}$

Ou seja, a força de maré na Lua provocada pela Terra é aproximadamente 20 vêzes a força de maré na Terra provocada pela Lua.

Rotação sincronizada e a evolução do sistema Terra-Lua

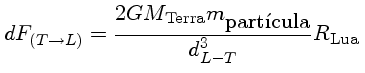
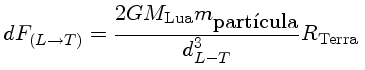
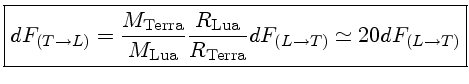
Acredita-se que, no passado, o período de rotação da Lua era menor do que o seu período de translação em torno da Terra. Ao girar, ela tentava arrastar consigo os bojos de maré, que sempre ficavam alinhados na direção da Terra. Assim, havia um movimento relativo entre as diferentes partes da Lua, o qual gerava atrito, que por sua vez tendia a frear a rotação. Devido a esse atrito a Lua foi perdendo energia de rotação até ficar com a rotação sincronizada, estado em que o período sideral é exatamente igual ao período de revolução.

Não é só a Lua que tem rotação sincronizada; os dois satélites de Marte, Phobos e Deimos, cinco luas de Júpiter (incluindo os quatro satélites galileanos), 9 luas de Urano, a lua Tritão de Netuno, Plutão e Caronte, todos têm rotação sincronizada. B>A maré de Júpiter sobre Io, que está aproximadamente à mesma distância de Júpiter que a Lua está da Terra, causa vulcanismo acentuado em Io, já que Júpiter tem massa 318 maior que a da Terra. A dissipação das forças de maré em Io causam o vulcanismo, e a órbita é mantida excêntrica por ressonância com Europa e Ganímedes, causando deslocamentos verticais de até 100 metros.

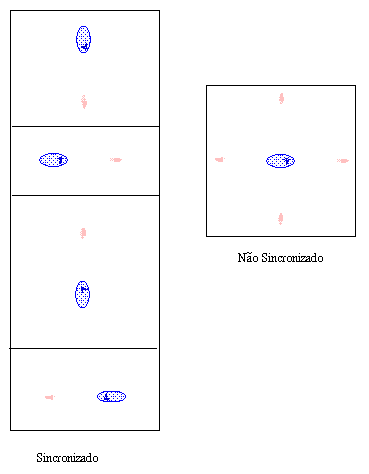
Na órbita circular e sincronizada não existe movimento relativo. A distorção ainda ocorre, mas há equilíbrio que não envolve qualquer movimento relativo por qualquer parte da matéria.

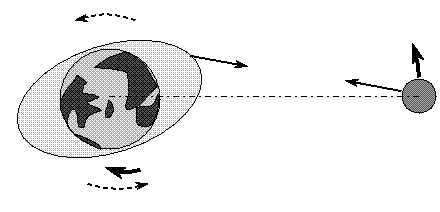
No estado atual de evolução do sistema Terra-Lua, a Terra ainda tem que girar sob os bojos de maré, que ficam sempre apontados para a Lua. O atrito gerado faz com que a rotação da Terra diminua, aumentando o dia em 0,002 segundos por século.

Se o momentum angular de rotação da Terra diminui por fricção, então a Lua tem que aumentar seu momentum angular orbital, movendo-se para mais longe da Terra.

Vamos ver porque isso acontece.

O momentum angular de translação da Lua é dado por , onde r é o raio da órbita e v a velocidade orbital. Aproximando por uma órbita circular, e o período , então:

ou seja, aumentando o raio da órbita r, aumenta o momentum angular orbital, compensando a redução do momentum angular de rotação (spin).

A força que "empurra" a Lua para fora é a gravidade exercida pelo bojo de maré mais próximo da Lua, que fica sempre um pouco "adiantado" em relação à Lua porque é arrastado junto com a Terra no movimento de rotação. A massa de água do bojo acelera a Lua, que ganha velocidade tangencial, se afastando da Terra.

A força gravitacional do bojo empurra a Lua para maiores distâncias.

No futuro distante, daqui a cerca de 15 bilhões de anos, a sincronização da órbita da Terra com a Lua implicará em que o dia e o mês terão a mesma duração, que será igual a aproximadamente 35 dias atuais! No passado, a Terra devia girar mais rápido e, portanto, o dia devia ser mais curto. De fato, estudos palentológicos indicam que 100 milhões de anos atrás o ano tinha 400 dias, o dia 21 horas, e as marés eram muito mais intensas, pois a Lua estava mais próxima. Atualmente a Lua está se afastando aproximadamente 3 cm por ano, que pode ser medido com a reflexão de feixes de laser no espelho deixado pelos astronautas na Lua. A evidência da mudança na duração do dia e ano vem de certas criaturas marinhas cujas conchas têm bandas de crescimento diários e mensais, permitindo que os cientistas contem os números de bandas em um ciclo mensal em fósseis de idades diferentes. No artigo de Charles P. Sonett, Erik P. Kvale, Aramais Zakharian, Marjorie A. Chan, Timothy M. Demko, "Late Proterozoic and Paleozoic Tides, Retreat of the Moon, and Rotation of the Earth" na Science vol 273, no. 5271, p. 100 de 05 de julho de 1996, eles apresentam indicações que o dia tinha somente 18 horas cerca de 900 milhões de anos atrás e a taxa de variação tem permanecido constante desde então.

Próxima: Limite de Roche Volta: Forças Gravitacionais Diferenciais

Astronomia e Astrofísica