Limite de Roche

Uma consequência das forças de maré é que um satélite em geral não pode chegar muito perto de seu planeta sem se romper. O limite de Roche é a distância mínima do centro do planeta que um satélite fluído pode chegar sem se tornar instável frente a rompimento por maré.

Em 1847, o astrônomo francês Edouard Albert Roche (1820-1883) demonstrou (Académie des Sciences et Lettres de Montepellier, Mémoires de la Section des Sciences, 1, 243) que, para um satélite fluído, mantido apenas por sua auto-gravidade, de densidade média

, orbitando em torno de um planeta de densidade média

e raio R, a distância mínima do planeta em que o satélite pode orbitar estavelmente é

Se o planeta e o satélite têm densidades iguais, o limite de Roche é 2,44 vezes o raio do planeta.

Uma derivação simplificada do limite se obtém considerando duas partículas de massas m iguais, e se tocando, isto é, separadas somente por uma distância dr. A força gravitacional entre as partículas é dada por:

e a força de maré de um corpo de massa M, e a uma distância d, sobre elas será:

Para as duas partículas permanecerem juntas, a força gravitacional entre elas tem que balançar a força de maré, logo

Seja

e

então

O valor da constante numérica, 2,51 ao invés de 2,44, é porque não levamos em conta que as partículas formam um fluído (têm força de van der Waals atuando entre as partículas, além da força gravitacional).

Em 1974, Hans R. Aggarwal e Vern R. Oberbeck (Astrophysical Journal, 191, 577) estudaram o caso de ruptura por maré de corpos esferoidais sólidos, rochosos ou gelados, mantidos coesos por forças de tensão intrínsecas de seu material. Encontraram que, para satélites desse tipo, com diâmetros maiores do que 40 km, a distância mínima que eles podem chegar de seu planeta sem quebrar é:

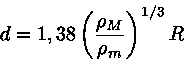
$d = 1,38({\rho_M \over \rho_m}\right)^{1/3} R$

Para corpos externos que se aproximam do planeta, a distância que eles podem chegar é ainda um pouquinho menor.

Questão: Qual a menor distância que a Lua pode chegar da Terra sem se romper?

Usando

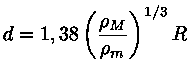
$d = 1,38\left(\frac{\rho_M}{\rho_m}\right)^{1/3} R$$

e considerando que:

$M_{\mathrm{Terra}} = 5,97 \times 10^{24}~\mathrm{Kg}$
$R_{\mathrm{Terra}} = 6\,370~\mathrm{Km}$
$M_{\mathrm{Lua}} = 7,35 \times 10^{22}~\mathrm{Kg}$
$R_{\mathrm{Lua}} = 1738~\mathrm{Km}$

Obtemos:

$\rho_{\mathrm{Terra}} = \frac{{M_\mathrm{Terra}}}{\frac{4}{3R_{\mathrm{Terra}}^3}} = 5514\,{\mathrm{kg/m^3}}$$

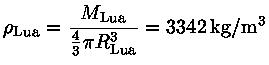
$\rho_{Lua} = \frac{{M_{Lua}}{\frac{4}{3R_{Lua}^3}} =3342 kg/m^3}$$

Portanto

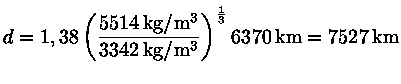
$d = 1,38 (\frac{5514{{kg/m^3}}}{3342{{kg/m^3}}} )^{\frac{1}{3}} 6370 km} = 7527 km}$$

Os satélites ou corpos impactantes podem ser quebrados por também outras causas, como por tensões aerodinâmicas, dependendo da densidade da atmosfera do planeta.

Enfim, os limites reais de aproximação mínima para os corpos serem estáveis frente a forças de maré dependem do tamanho e tensão interna dos corpos. Satélites sólidos podem chegar mais perto do planeta do que satélites fluidos porque as forças de tensão interna das rochas que o constituem o mantêm estável. Corpos menores do que 40 km podem chegar ainda mais perto do planeta sem quebrar por forças de maré desde que eles sejam pequenos e duros o suficiente. Por exemplo, os anéis de Saturno estão dentro do limite de Roche de Saturno, o que significa que as pequenas partículas que formam o anel têm forças coesivas maiores do que as forças de maré. Entretanto, à medida que aumenta o tamanho da partícula, suas forças coesivas ficam menos importantes comparadas com as forças de maré, e essa é uma provável explicação para o fato dessas partículas nunca terem se juntado para formar um satélite. É possível que os anéis de Saturno sejam resultado de um satélite ou cometa que se aproximou demais do planeta e se quebrou devido às forças de maré.

A lua Tritão, de Netuno, descoberta em 10 de outubro de 1846 por William Lassell (1799-1880), 17 dias depois da descoberta de Netuno, têm 2700 km de diâmetro, densidade de 2061 kg/m³, a=354 759 km, período orbital de 5d21h, órbita retrógrada e composição parecida com a de Plutão, e é provavelmente um asteróide capturado por Netuno, pois está se aproximando de Netuno, de modo que em 3,6 bilhões de anos vai estar dentro do limite de Roche, quando se romperá, provavelmente formando um anel.

Simulação da disrupção de uma estrela pelo buraco negro central da galáxia RX J1242-11, observada pelos satélites Chandra (NASA), XMM-Newton (ESA), e ROSAT (Alemanda).

Várias galáxias que observamos em colisões com outras galáxias mostram o efeito da força de maré causando o desmembramento das galáxias.

Próxima: Precessão Volta: Forças Gravitacionais Diferenciais

Astronomia e Astrofísica