Em coordenadas cartesianas:
r12 = (x + ae)2 + y2
(a)
r2 = (x - ae)2 + y2
(b)
Subtraindo-se (a) - (b), temos:
r1 = a + ex
(c)
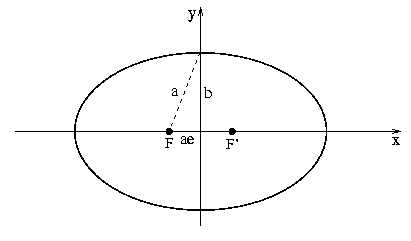
Levando-se em conta que
o semi-eixo menor é dado por
b2 = a2(1 - e2),
o que pode
ser facilmente derivado pelo teorema de Pitágoras colocando-se
o ponto P(r,θ)
em θ=90°
e substituindo-se em (c) em (a), temos
a equação de uma elipse em coordenadas cartesianas:
x =
a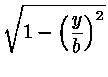
A área da elipse é dada por:
A = 4
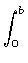 dy
dy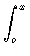 dx
dx.
A = 4
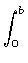 a
a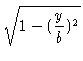
d
y,
Substituindo-se y = bsin z, e
dy = bcosz dz,
A = 4
ab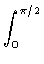
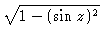
cos
z d
z
e como
sin2z + cos2z = 1, logo
1 - sin2z = cos2z,
resulta:
A = 4
ab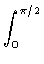
cos
2z d
z.
Como
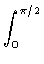
cos
2z d
z =

/4,
![[*]](voltas.gif)
![[*]](ants.gif)
Volta: Leis de Kepler Generalizadas
Anterior: Apêndice
 Marés
Marés
 Astronomia e Astrofísica
Astronomia e Astrofísica
©
Modificada em 5 abril 2000
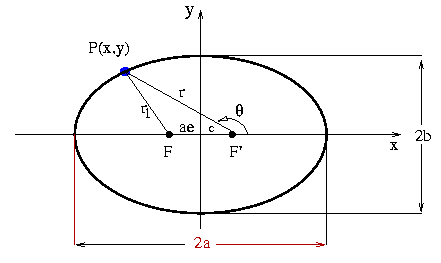
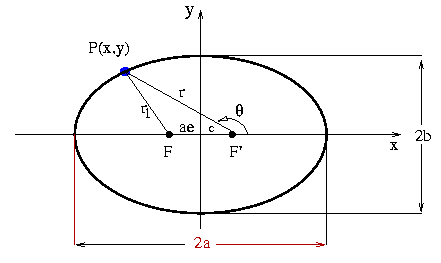
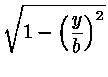
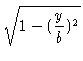 dy,
dy,
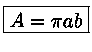
![[*]](voltas.gif)
![[*]](ants.gif)