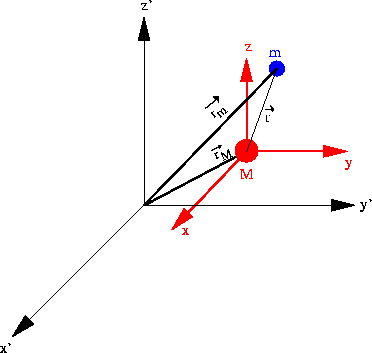
 Da lei da gravitação se pode derivar as leis de Kepler. Aplicando-se
a lei da gravitação e a segunda lei do movimento
(
Da lei da gravitação se pode derivar as leis de Kepler. Aplicando-se
a lei da gravitação e a segunda lei do movimento
(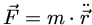 ),
temos:
e pela lei da ação e reação,
onde
e
),
temos:
e pela lei da ação e reação,
onde
e 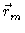 e
e 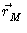 são os vetores posição de m e M
com relação a um sistema inercial.
são os vetores posição de m e M
com relação a um sistema inercial.
Estas equações podem ser escritas como:
Subtraindo-se estas duas equações:
Definindo-se μ=G(m + M),
podemos escrever:
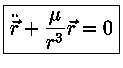
(1)
Esta é a equação diferencial vetorial do movimento relativo de
dois corpos.
A solução desta equação nos dá a
órbita relativa dos
corpos (planeta, cometa, satélite, etc).
Em princípio, a solução
descreve como o raio vetor 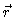 varia com o tempo, mas sua solução
não é simples. Como a equação é
diferencial vetorial de segunda ordem,
isto é, envolve segunda derivada de vetores, precisamos de seis
constantes para obter a
solução.
Por exemplo, se soubermos a posição tridimensional e
a velocidade de um planeta num certo tempo,
poderemos calcular sua posição
e velocidade em qualquer outro tempo.
varia com o tempo, mas sua solução
não é simples. Como a equação é
diferencial vetorial de segunda ordem,
isto é, envolve segunda derivada de vetores, precisamos de seis
constantes para obter a
solução.
Por exemplo, se soubermos a posição tridimensional e
a velocidade de um planeta num certo tempo,
poderemos calcular sua posição
e velocidade em qualquer outro tempo.
Nossa solução envolve demonstrar que a
conservação da energia e do momentum angular
são conseqüências das leis de Newton.
![[*]](proxs.gif)
![[*]](voltas.gif)
Próxima: Conservação da Energia Total do Sistema
Volta: Leis de Kepler Generalizadas
©
Modificada em 6 Abril 2000
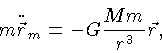

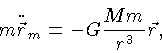
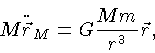
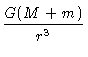
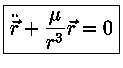 (1)
(1)
![[*]](proxs.gif)
![[*]](voltas.gif)