Lembrando que para dois vetores 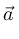 e
e
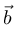 formando um ângulo α entre eles:
formando um ângulo α entre eles:
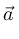
⋅
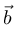
= |
a| |
b| cos α
O produto vetorial × resulta em um vetor perpendicular ao vetor 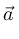 e ao
vetor
e ao
vetor 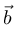 , normal ao plano contendo os dois vetores, de módulo:
, normal ao plano contendo os dois vetores, de módulo:
|
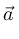
×
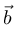
| = |
a| |
b| sen α
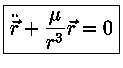
(1)
Multiplicando-se a equação (1) escalarmente por
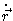 temos:
temos:
Como
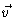 =
= 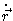 e
e
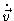 =
=  temos:
Seja α
o ângulo entre o raio vetor e a velocidade:
temos:
Seja α
o ângulo entre o raio vetor e a velocidade:
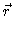 .
. 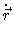
=
r v cos
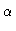
e
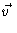 .
. 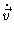
=
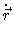 .
. 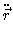
=
v 
cos(-
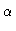
)
e cos(-α)=cos(α), eliminando cos(α) dos dois termos.
Como dxn=n dx(n-1),
o primeiro termo da equação pode ser escrito como
e o segundo termo da equação:
de modo que podemos escrever nossa equação como:
de onde se conclui imediatamente que o termo derivado é uma constante, já que sua derivada é nula:
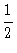 v2
v2 -
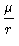
= ε
= constante
(
2)
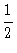 v2
v2 -
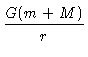
=ε = constante
que é a equação de energia do sistema
(ε = energia por unidade de massa)
![[*]](proxs.gif)
![[*]](voltas.gif)
![[*]](ants.gif)
Próxima: Conservação do momentum angular
Volta: Leis de Kepler Generalizadas
Anterior: Equação do movimento
©
Modificada em 15 out 2024
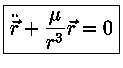 (1)
(1)
![]() temos:
temos:
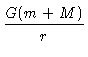 =ε = constante
=ε = constante
![[*]](proxs.gif)
![[*]](voltas.gif)
![[*]](ants.gif)