A lei da gravitação universal, que relaciona
a força entre duas massas M e m, separadas
por ![]() , derivada por Newton é dada por:
, derivada por Newton é dada por:
![]()
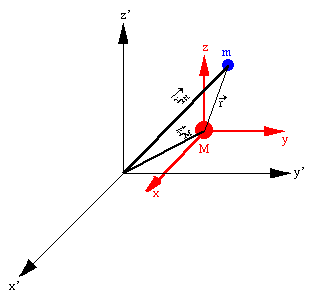
Desta lei se pode derivar as leis de Kepler. Aplicando-se
a lei da gravitação e a segunda lei do movimento
(![]() ),
temos:
),
temos:
![]()
e pela lei da ação e reação,
![]()
onde
![]()
e ![]() e
e ![]() são os vetores posição de m e M
com relação a um sistema inercial.
são os vetores posição de m e M
com relação a um sistema inercial.
Estas equações podem ser escritas como:
![]()
![]()
Subtraindo-se estas duas equações:
![]()
Definindo-se ![]() ,
podemos escrever:
,
podemos escrever:
![]()
Esta é a equação diferencial vetorial do movimento relativo
dos corpos de massa m e M.
A solução desta equação nos dá a órbita relativa
dos corpos
(planeta, cometa, satélite). Em princípio a solução
nos dá
como o raio vetor varia com o tempo, mas não podemos escrever uma
solução envolvendo funções familiares diretamente. Como esta
equação é diferencial vetorial de segunda ordem, isto é,
envolve segunda derivativa de vetores, precisamos de 6 constantes
para obter a solução. Por exemplo, se soubermos a posição
tridimensional e a velocidade de um planeta, poderemos calcular
sua posição e velocidade em qualquer outro tempo.
Nossa solução, mais geral, envolve demonstrar quantidades físicas, como a conservação da energia e do momento angular.
![]() Introdução à Astronomia e à
Astrofísica
Introdução à Astronomia e à
Astrofísica
