A Tabela de Posições dá as longitudes heliocêntricas ![]() e
e
![]() ,
da Terra e de Marte respectivamente, e a elongação
,
da Terra e de Marte respectivamente, e a elongação
![]() de Marte, para 24 datas.
de Marte, para 24 datas.
Primeira Lei. O problema consiste em traçar a órbita de
Marte a partir das várias posições na tabela. Em um cálculo
preliminar, Kepler encontrou que a Terra tinha uma órbita quase
circular com excentricidade e = 0,017, e longitude no periélio
de ![]() .
.
1. Desenhe esta órbita, usando um círculo de raio r. Coloque a
posição do Sol a uma distância ![]() do centro do círculo
na direção do periélio.
do centro do círculo
na direção do periélio.
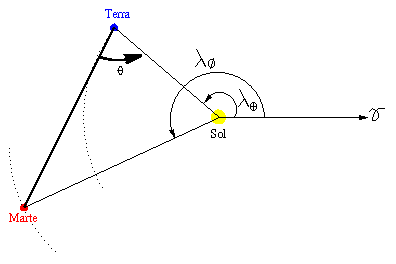
2. Agora plote as posições de Marte, como segue:
Desenhe a
direção (vamos chamar ![]() essa direção), que é comum para Terra e Marte na oposição
essa direção), que é comum para Terra e Marte na oposição ![]() 1.
Note que neste ponto só sabemos a direção em que está Marte,
mas não sabemos em que posição ao longo desta direção ele está.
No entanto, após 1 período sideral, P, em julho de 1958, Marte retornou
à mesma longitude. Sua posição
1.
Note que neste ponto só sabemos a direção em que está Marte,
mas não sabemos em que posição ao longo desta direção ele está.
No entanto, após 1 período sideral, P, em julho de 1958, Marte retornou
à mesma longitude. Sua posição ![]() agora pode ser encontrada
plotando a posição da Terra no diagrama, e então desenhando
a linha (vamos chamar
agora pode ser encontrada
plotando a posição da Terra no diagrama, e então desenhando
a linha (vamos chamar ![]() ), na direção dada pelo ângulo
), na direção dada pelo ângulo ![]() .
O ponto em que essa linha corta a linha
.
O ponto em que essa linha corta a linha ![]() é a posição de Marte.
é a posição de Marte.
Da mesma forma, as posições ![]() ,
,![]() ,...,
,...,![]() de Marte na
sua órbita podem ser encontradas para as longitudes correspondentes
às 12 oposições listadas na tabela.
de Marte na
sua órbita podem ser encontradas para as longitudes correspondentes
às 12 oposições listadas na tabela.
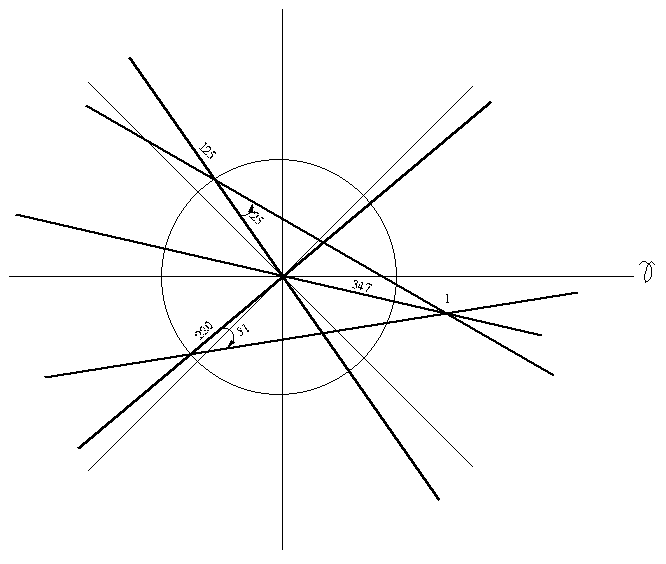
4. Determine o comprimento do semi-eixo maior em unidades astronômicas, a excentricidade orbital, e, e a longitude do periélio.
Terceira Lei.
5. O período sinódico, S, pode ser encontrado a partir do
intervalo médio entre oposições sucessivas. Calcule este valor
para cada par de oposições listadas na tabela.
Exemplo: ![]() = 36523-35726=797 dias. É preciso calcular o valor médio.
= 36523-35726=797 dias. É preciso calcular o valor médio.
6. Calcule o período sideral de Marte, P, em dias e em anos.
O período sideral é o intervalo de tempo entre longitudes iguais sucessivas!
Exemplo: ![]() = 687 dias. Mais fácil ainda é utilizar o
período sinódico médio calculado na questão
anterior e a relação
entre o período sinódico e o período sideral.
Mostre que a razão
= 687 dias. Mais fácil ainda é utilizar o
período sinódico médio calculado na questão
anterior e a relação
entre o período sinódico e o período sideral.
Mostre que a razão ![]() é a mesma para a Terra e para Marte.
é a mesma para a Terra e para Marte.
Segunda Lei. Kepler observou que o movimento longitudinal de
Marte era irregular. Entre duas oposições sucessivas, separadas
por um intervalo ![]() , a longitude cresce de
, a longitude cresce de
![]() . A velocidade angular resultante,
. A velocidade angular resultante,
![]() , não era constante.
Exemplo: entre 1a. e 2a. oposição,
, não era constante.
Exemplo: entre 1a. e 2a. oposição,
![]() = 797 - 687 = 110 dias,
= 797 - 687 = 110 dias, ![]() , e portanto
, e portanto ![]()
7. Plote a variação de ![]() como uma função
da longitude
como uma função
da longitude ![]() .
Use a longitude média no intervalo.
Que direções correspondem aos
valores de máximo e mínimo? Para estas duas direções
mostre que a área varrida pela linha unindo Marte e o Sol na unidade
de tempo é sempre a mesma, lembrando que a velocidade areal é
dada por:
.
Use a longitude média no intervalo.
Que direções correspondem aos
valores de máximo e mínimo? Para estas duas direções
mostre que a área varrida pela linha unindo Marte e o Sol na unidade
de tempo é sempre a mesma, lembrando que a velocidade areal é
dada por:
![]()
Referência: Kleczek J. & Minnaert M.G.J. 1987, Exercises in Astronomy.
![]()
![]()