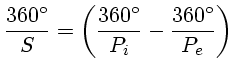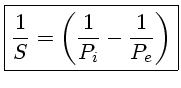- Período sinódico (S):
- é o intervalo de tempo decorrido entre
duas configurações iguais consecutivas. É o período de revolução
aparente do planeta, em relação à Terra.
- Período sideral (P):
- é o período real de translação do
planeta em torno do Sol, em relação a uma estrela fixa.
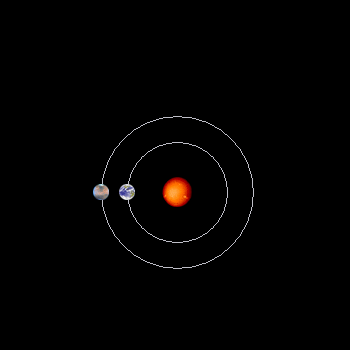
Órbitas da Terra e de Marte em torno do Sol, de oposição a oposição.
Não está em escala.
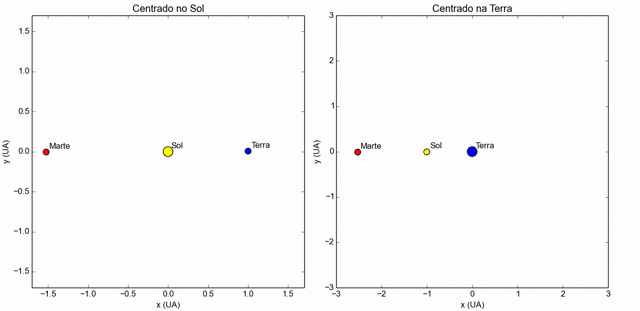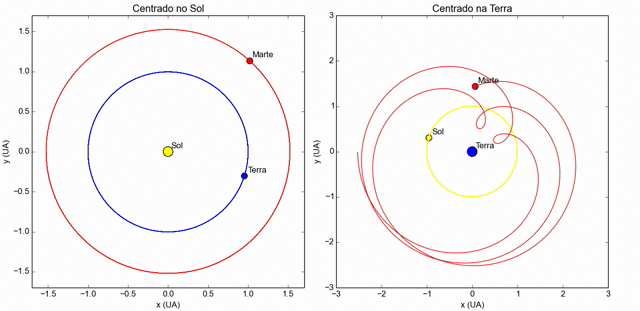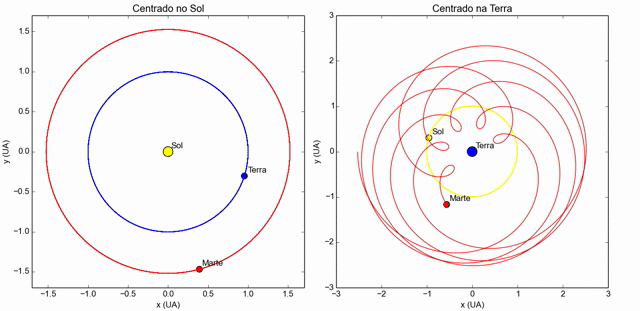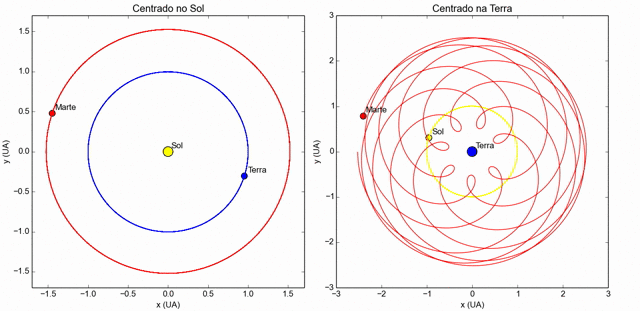
Relação entre os dois períodos
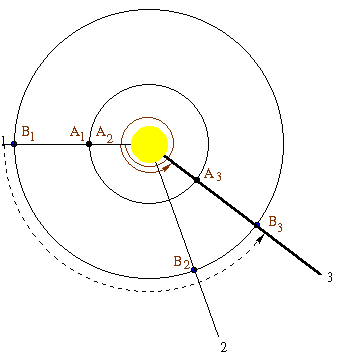
Considere dois planetas, A e B, com A movendo-se
mais rápido por estar numa órbita menor e, portanto, mais interno do que o planeta B. Na posição
(1), o planeta A passa entre o planeta B e o Sol. O planeta B está
em oposição visto do planeta A, e o planeta A está em
conjunção inferior se visto do planeta B. Quando
A completou uma revolução em torno do Sol e retornou
à posição (1), B se moveu para a posição
(2). De fato, A não alcança B até que os dois
planetas alcançem a posição (3). Agora o planeta mais interno
A ganhou uma volta completa (360°) a mais que o planeta B.
Para achar a relação entre o período sinódico e o período
sideral, vamos chamar de 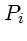 o período sideral do planeta interior,
e de
o período sideral do planeta interior,
e de 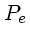 o período sideral do planeta exterior.
o período sideral do planeta exterior. 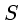 é o período
sinódico (aparente), que é o mesmo para os dois.
é o período
sinódico (aparente), que é o mesmo para os dois.
O planeta interior, movendo-se
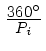 por dia, viaja mais
rápido do que o planeta exterior, que se move a
por dia, viaja mais
rápido do que o planeta exterior, que se move a
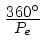 por dia.
por dia.
Após um dia, o planeta interior terá ganho um ângulo de
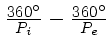 em relação ao planeta
exterior. Por definição de período sinódico,
esse ganho é
igual a
em relação ao planeta
exterior. Por definição de período sinódico,
esse ganho é
igual a
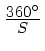 , já que em S
dias esse ganho será igual
a 360°.
Ou seja:
, já que em S
dias esse ganho será igual
a 360°.
Ou seja:
que é o mesmo que:
Exemplos de períodos
- Marte esteve em oposição em 8 de dezembro 2022 e novamente em 16 de janeiro de 2025.
Sabendo-se que Marte leva 780 dias para nascer quando o Sol se põe
(estar em oposição) duas vezes seguidas, qual é o período sideral (orbital) de Marte?
Usamos a fórmula
identificando que, neste caso, I=Terra e PI=1 ano,
E=Marte e S=780 dias/(365,25 dias/ano) = 2,136 anos,
já que o período entre duas oposições é o
período sinódico S.
Calculado-se
obtém-se que o período sideral de Marte é PE=1,88 anos = 687 dias.
- Sabendo-se que Vênus leva 583,93 dias para aparecer em
elongação
máxima a leste duas vezes seguidas (se põe ≈3 horas depois do Sol)
qual seu período sideral (orbital)?
Usamos a fórmula
identificando que, neste caso, E=Terra e PE= 365,25 dias,
I=Vênus e S=583,93 dias,
já que o período entre duas elongações máximas a leste é o
período sinódico S.
Calculado-se
obtém-se que o período sideral (em torno do Sol) de Vênus PI= 224,7 dias = 0,6152 anos.
Próxima: Distâncias dentro do Sistema Solar
Volta: Movimento dos Planetas
 Astronomia e Astrofísica
Astronomia e Astrofísica
 ©
©
Modificada em 26 mar 2025


![]() por dia, viaja mais
rápido do que o planeta exterior, que se move a
por dia, viaja mais
rápido do que o planeta exterior, que se move a
![]() por dia.
por dia.
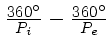 em relação ao planeta
exterior. Por definição de período sinódico,
esse ganho é
igual a
em relação ao planeta
exterior. Por definição de período sinódico,
esse ganho é
igual a
![]() , já que em S
dias esse ganho será igual
a 360°.
Ou seja:
, já que em S
dias esse ganho será igual
a 360°.
Ou seja: